Умножение, деление и степенуване на едночлени.

Вече се запознахме с понятието едночлен и научихме кои едночлени са подобни и как да ги събираме и изваждаме. Време да се научим на останалите действия с едночлени, а именно- умножение, деление и степенуване на едночлени. Правилата са лесни и много приятни, ако сме си научили уроците дотук!
Умножение на едночлени
Нека умножим тези два едночлена:
А = 2ab и B = 6abx
Прилагаме разместителното свойство на умножението, както и правилата за степенуване:
A . B = (2ab).(6abx) = (2.6).(a.b.a.b).x = 12a2 b2 x
Разбира се не е нужно всеки път да групираме по този начин множителите в скоби, можем веднага да запишем краен отговор. Важното е да “подредим” едночлена като започнем от числовата константа и след това запишем буквите в азбучен ред със съответните им степени т.е. да го приведем в нормален вид.
А сега да умножим следните два едночлена:
M = 7abx4 и N = 30b2x7
Произведението им е равно на:
M.N = (7abx4).(30b2x7) = 210ab3x11

Произведението на едночлени е едночлен! При умножението на едночлени привеждане произведението им в нормален вид.
Степенуване на едночлени
За да степенуваме едночлен, използваме правилото на степенуване на произведение. Достатъчно да “повдигнем” на съответната степен всеки множител на едночлена.
Нека запишем на колко е равен А3 , ако А = 4ab2
А3 = (4ab2)3 = 43a3b6
Всъщност ние сме степенували едночлени още в 6-ти клас. Сега допълваме знанията си с нови понятия. Нека степенуваме още един едночлен: M = 0,1a2bxy4
Сега запишем на колко е равен едночленът на втора степен, а след това- на трета.
M2 = (0,1a2bxy4)2 = 0,01a4b2x2y8
M3 = (0,1a2bxy4)3= 0,001a6b3x3y12
Ако сте забравили правилата за степенуване, може да си ги припомните в секцията 6.клас.

Степента на едночлен е също едночлен, когато степенният показател е естествено число. При степенуването на едночлен го привеждаме в нормален вид.
Деление на едночлени
Да разделим два едночлена, като не забравяме, че можем с дробна черта да заменим знака за деление.
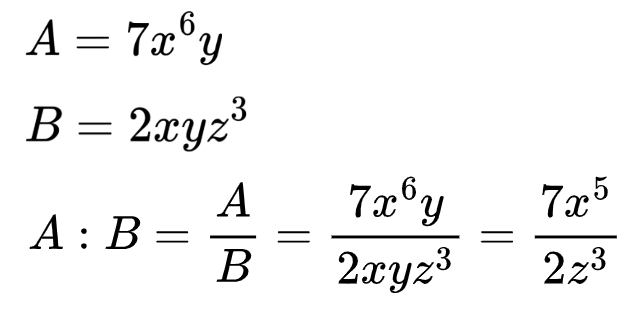
Хайде да разгледаме още един пример с деление на едночлени!
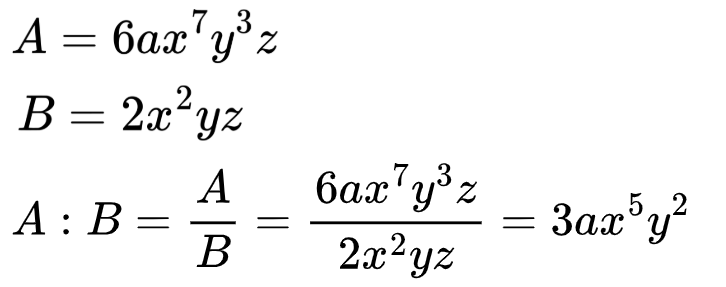
За разлика от умножението и степенуването, при делението на едночлени не винаги се получава едночлен.
Нека решим следващия пример:
Намерете частното на следните едночлени: P = 24ax5y и N = 3-1x3y
P : N = (24ax5y):(3-1x3y)
Можем да използваме дробна черта, за да улесним изчисленията си:
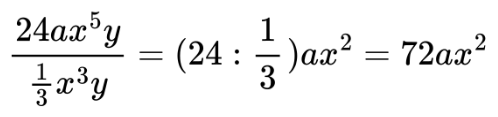

Запомнете, че частното на два едночлена невинаги е едночлен!
Намиране на неизвестен едночлен
Когато търсим неизвестен едночлен, прилагаме правилата за намиране на неизвестно число. Тях вече познаваме от решаването на уравнения.
Пример №1:
Да намерим неизвестния едночлен в равенството:
24abx4 = V : 0,5axy2
Ако ви е трудно да се сетите как да намерите едночлена, може да замените знакът за деление с дробна черта и да съставите пропорция:
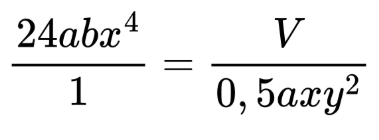
След това използваме основното свойство на пропорциите и можем да умножим “на кръст” членовете на пропорцията.
V.1 = (24abx4).(0,5axy2)
V = 12a2bx5y2
Пример №2:
Отново трябва да намерим неизвестния едночлен в равенството:
u . 0,5аxy8 = 14ax2y9
Едночленът тук е неизвестен множител. За да го намерим, трябва да разделим произведението на дадения множител.
u = 14ax2y9:0,5аxy8
Можем да заменим делението с дробната черта, за да ни е по-лесно:
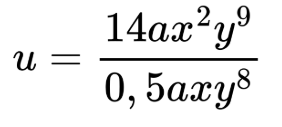
След извършването на делението получаваме:
у = 28xy
Пример №3
И за финал на днешния урок нека извършим приведение и да намерим числената стойност на израза A = 0,7xy2 + 2,1xyy — 4y.(—2xy)
за x = —1 и y = 0,5
Извършваме приведение като привеждаме едночлените в нормален вид, ако те не са в такъв и събираме подобните едночлени. Получаваме:
А = 0,7xy2 + 2,1xy2 + 8xy2 = 10,8xy2
Сега да заместим x и y със съответните стойности:
А = 10,8.(—1).0,52 = — 2,7
Обобщение

Умножението на едночлени и степенуването на едночлени със степенен показател естествено число се свеждат до привеждане на едночлените в нормален вид.
Деление на едночлени извършваме като разделим техните числови константи, а за буквената част прилагаме правилата за степенуване.
Може да се упражните със следващия тест!
Ако искаш да си припомниш всички изучени до момента действия с едночлени, изгледай видеото долу:







