Представете си, че сте изследователи, които се подготвят да открият съкровище! На вашата карта е нарисуван триъгълник – но не какъв да е триъгълник, а такъв, в който трите му височини сочат мястото на съкровището! Точно така – днес ще се запознаем с височините в триъгълника и ще научим как да ги използваме, за да открием неговите интересни свойства.

1. Теоретична част

1.1. Какво е триъгълник и какви видове има?

Триъгълникът е геометрична фигура, която има три страни и три върха. Той е една от основните форми в геометрията и има много приложения в различни науки. Триъгълниците могат да се разделят на видове според страните и ъглите си:

• Според страните:
  • Равностранен триъгълник – има три равни страни и три равни ъгли.
  • Равнобедрен триъгълник – има две равни страни и два равни ъгъла.
  • Разностранен триъгълник – има три различни страни и три различни ъгъла.
• Според ъглите:
  • Остроъгълен триъгълник – всички ъгли са остри (по-малки от 90 градуса).
  • Правоъгълен триъгълник – има един прав ъгъл (точно 90 градуса).
  • Тъпоъгълен триъгълник – има един тъп ъгъл (по-голям от 90 градуса).

2. Височини в триъгълника

2.1. Какво е височина?

Височината в триъгълника е перпендикуляр, спуснат от върха към срещуположната страна или продължението ѝ. Височините на триъгълника играят важна роля и имат интересни свойства.

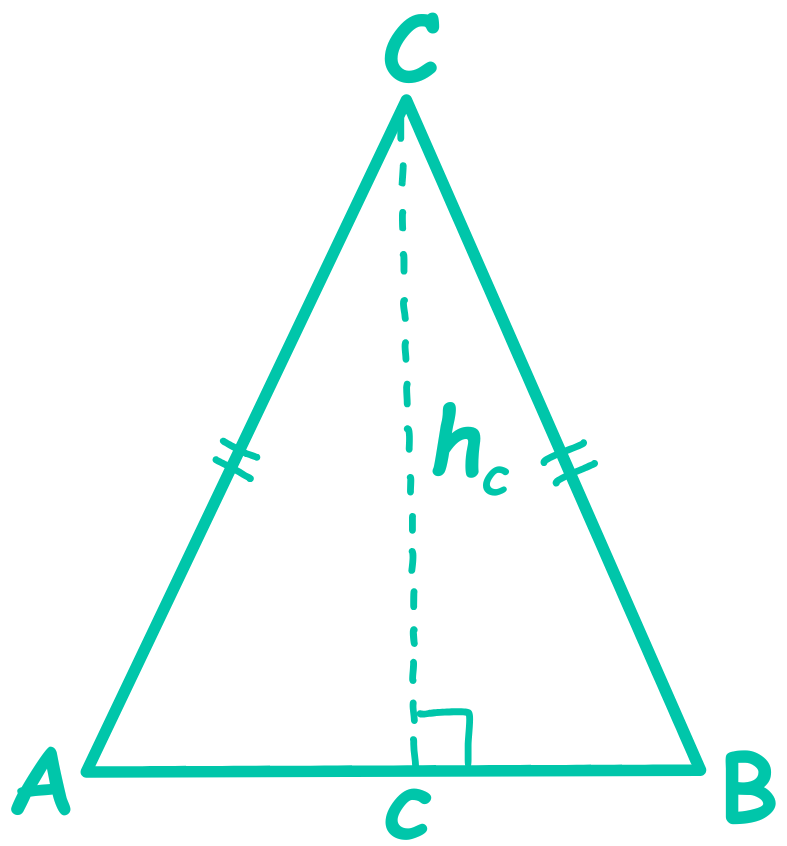
2.2. Свойства на височините:

1. Всеки триъгълник има три височини, всяка от които излиза от един от върховете му.
2. Височините се пресичат в една обща точка, която се нарича ортоцентър. Ортоцентърът може да бъде вътре в триъгълника, ако той е остроъгълен, да съвпада с връх на триъгълника, ако е правоъгълен, и извън триъгълника, ако е тъпоъгълен.

В триъгълника ABC са построени перпендикуларни прави през върховете A, B и C към срещуположните страни:

t_a ┴ BC

t_b ┴ AC

t_c ┴ AB

t_{a ,}t_b и t_c са височини в триъгълника

Забележка: В повечето означения към задачи можеш да срещнеш височината, към дадена страна, да се бележи с латинската буква “h“.

2.3. Как да начертаем височините на триъгълника?

1. Изберете върха, от който ще начертаете височината.
2. Спуснете перпендикуляр от този връх към срещуположната страна.
3. Повторете същото за останалите два върха.

2.3.1. Построяване на височини в остроъгълен триъгълник

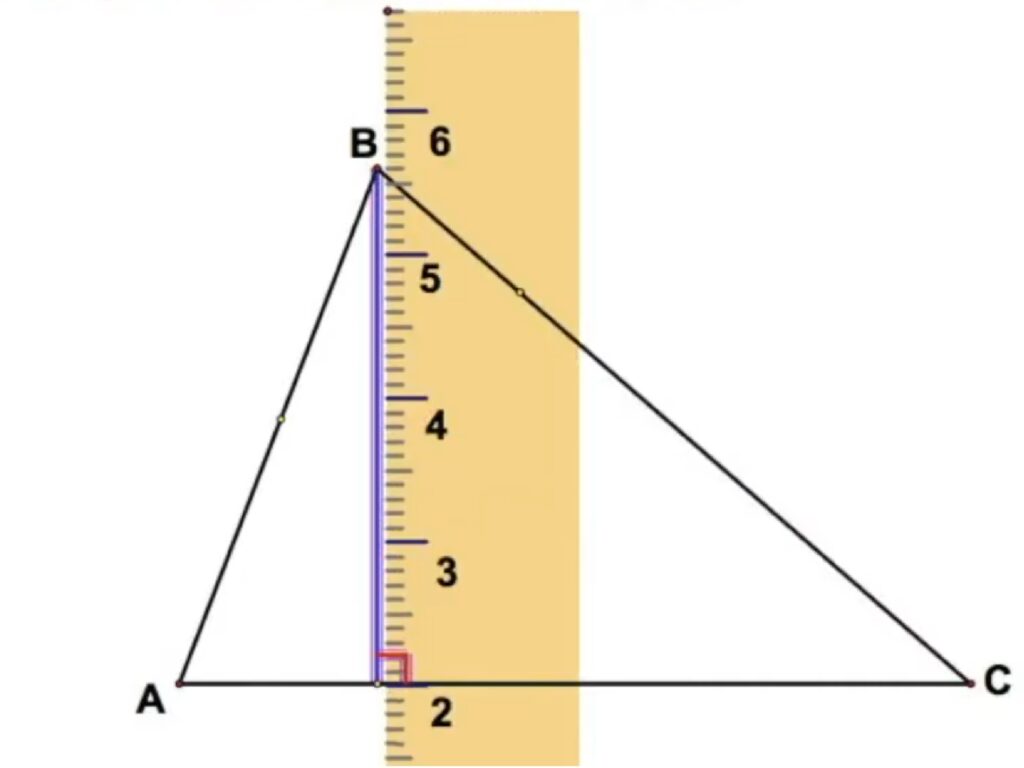
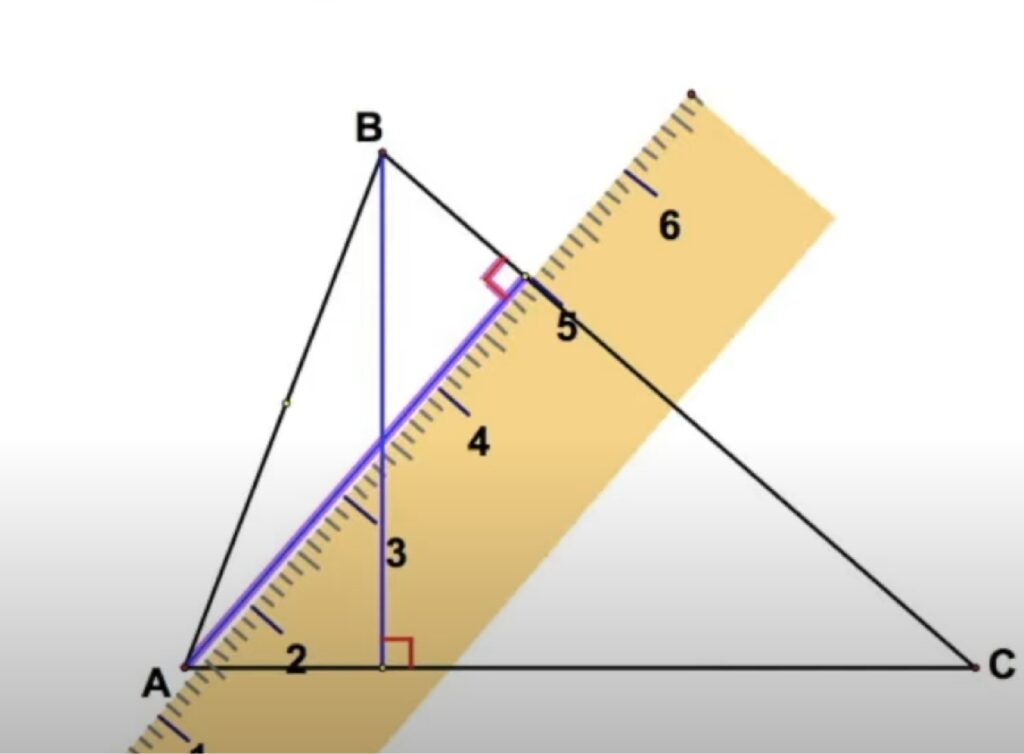
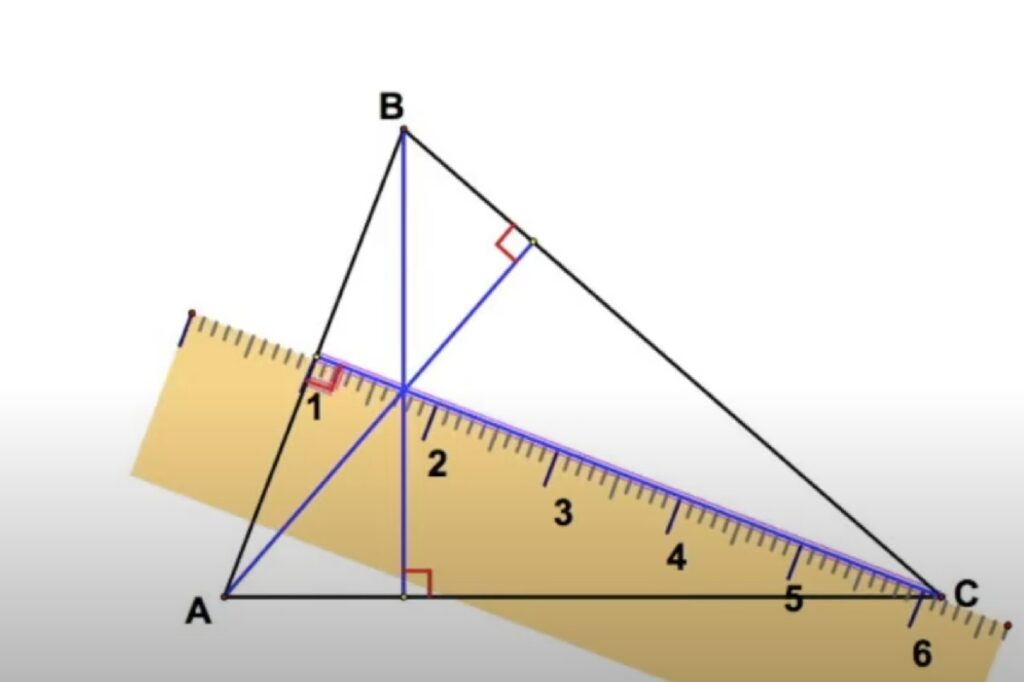
2.3.2 Построяване на височини в тъпоъгълен триъгълник

1. Продължаваме страната към която искаме да построим височина.

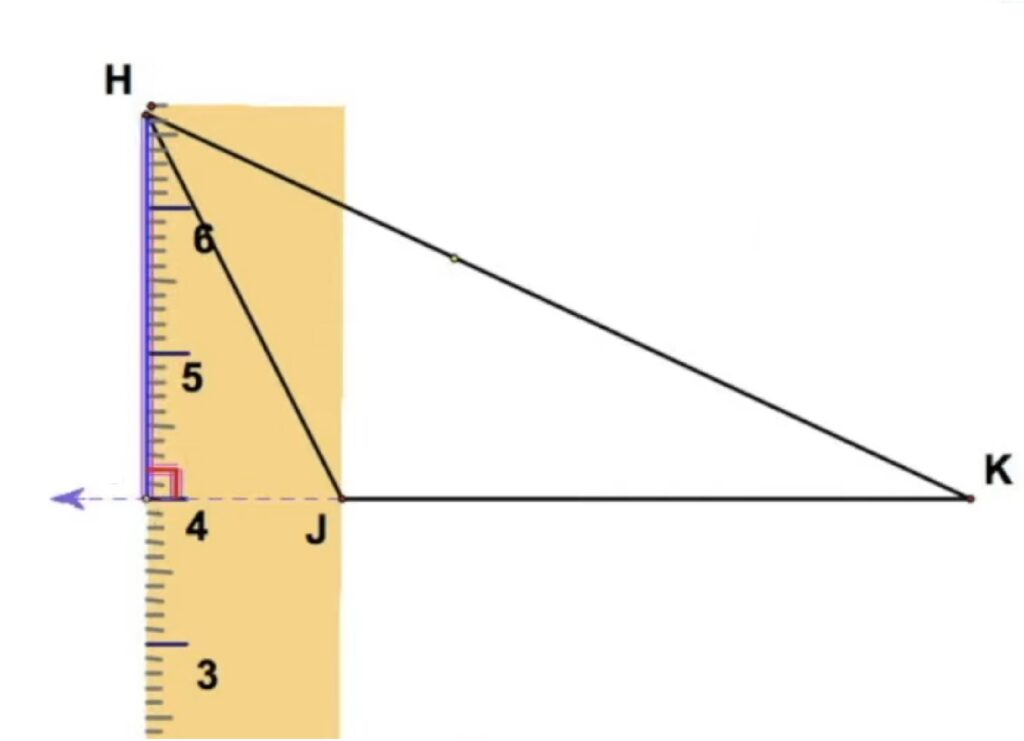
2. Намираме срещулежащия й връх и от него спускаме перпендикуляр.

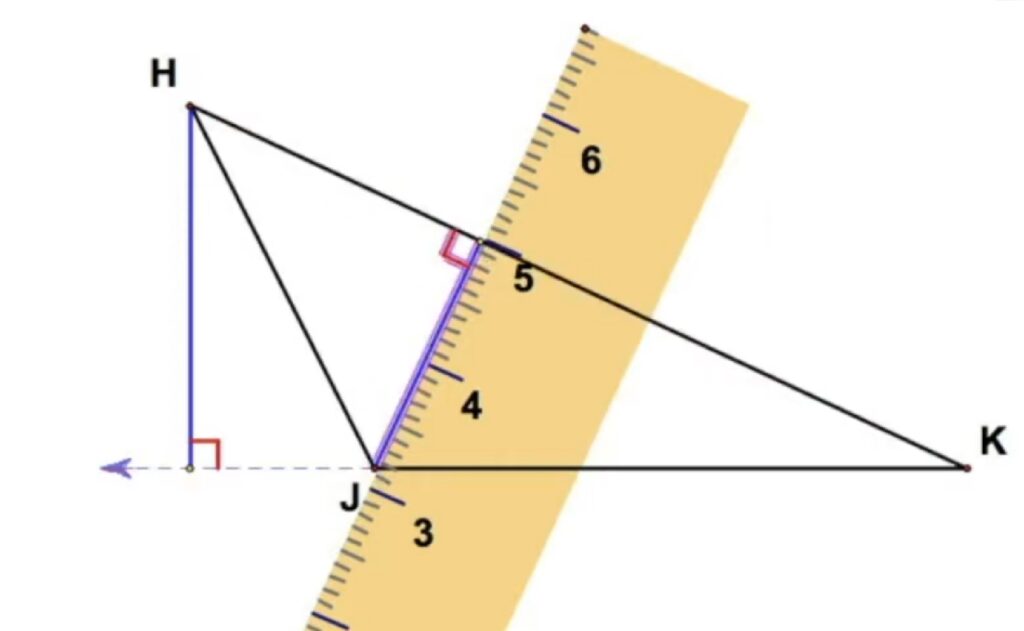
3. Построяваме височината, която е разположена вътре в триъгълника.

4. Удължаваме другата страна към която искаме да построим височина.

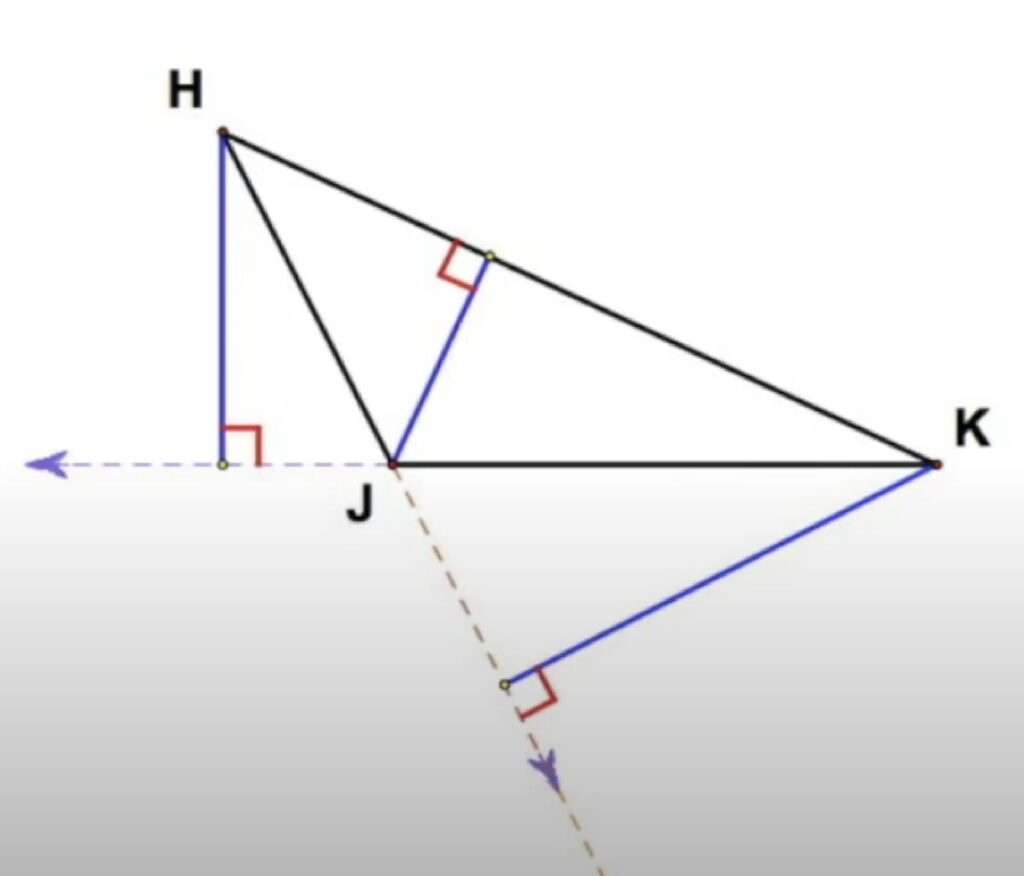
5. Намираме срещулежащия й връх и от него спускаме перпендикуляр.

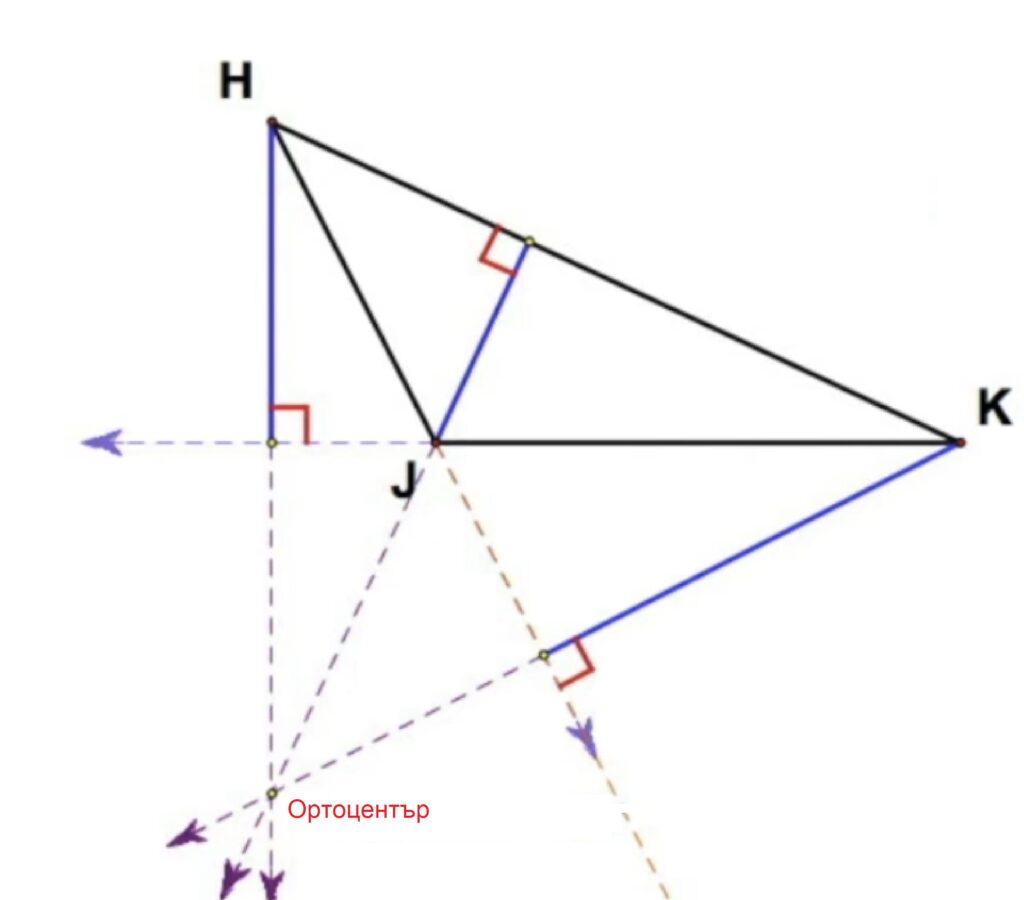
6. Удължаваме височините до пресичането им в една обща точка (ортоцентър).

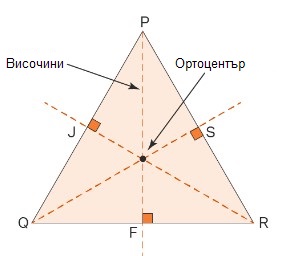
3. Височини в остроъгълен триъгълник

В остроъгълен триъгълник трите построени височини се намират в триъгълника. Ортоцентърът е вътрешен за триъгълника.

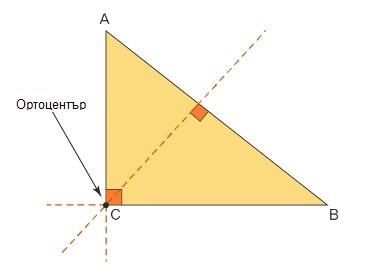
4. Височини в правоъгълен триъгълник

В правоъгълен триъгълник височината към хипотенузата (най-дългата страна, намираща се срещу правия ъгъл) му се намира вътре в триъгълника, а другите две височини съвпадат с двата му катета (страните, прилежащи до правия ъгъл на триъгълника). Ортоцентърът съвпада с един от върховете на триъгълника (т. е. C).

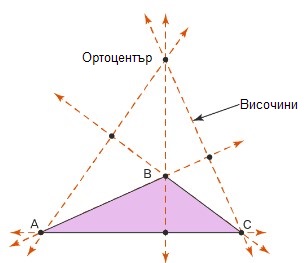
5. Височини в тъпоъгълен триъгълник

В тъпоъгълен триъгълник една от височините му се намира вътре в триъгълника, а другите две са извън него.Ортоцентърът е извън триъгълника.

6. Примерни задачи за упражнение

1. Теоретична задача:
   • Начертайте триъгълник ABC и обозначете върховете му. Намерете и отбележете височините му. Къде се намира ортоцентърът на този триъгълник? Какво ще забележите, ако триъгълникът е остроъгълен или тъпоъгълен?
2. Практическа задача:
   • Измерете размерите на един триъгълник, който сте начертали, и отбележете височините му. Ако искате да направите „геометрично съкровище“, нарисувайте карта, където височините на триъгълника показват мястото на съкровището.
3. Логическа задача:
   • Представете си, че имате равностранен триъгълник със страна 5 cm. Каква ще е дължината на всяка височина? Ще се пресичат ли височините на същото място?

7. Заключение

Триъгълниците са не само интересни геометрични фигури, но и имат уникални свойства, които можем да използваме в ежедневието и в науката. Височините им разкриват много от тези свойства, затова е забавно и полезно да ги разберем и използваме.