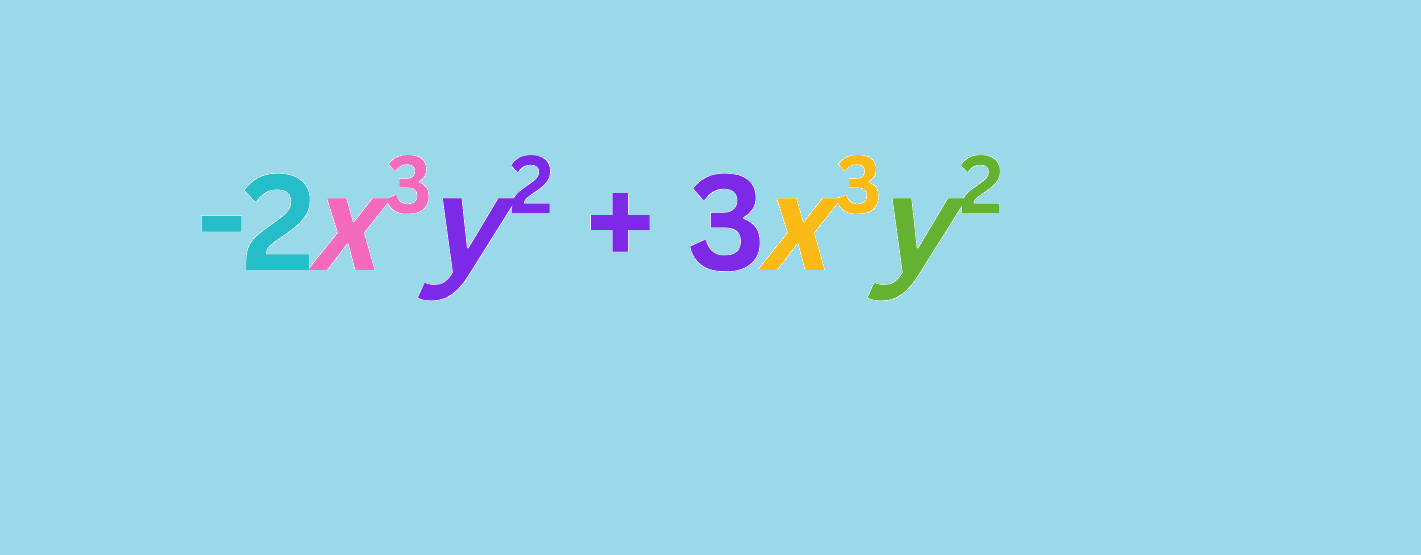Събиране и изваждане на едночлени. Подобни едночлени.
Здравей, бъдещ математико!
Замислял ли си се как събираме ябълки и круши? Не ги смесваме – просто казваме колко броя от всеки вид плод имаме. Така е и в алгебрата! Не можем да събираме всякакви изрази, но можем лесно да събираме и изваждаме подобни едночлени. Готов ли си да разбереш как?
1. Какво е едночлен?
Нека си припомним какво беше едночлен:

Едночлен е израз, който съдържа число, променливи (букви) и техни степени, които се умножават помежду си.
Примери:
- 3x
- −2x2y
- 5 (това също е едночлен – само число!)
2. Какво значи “подобни едночлени”? 🔍

Подобни едночлени са такива, които имат едни и същи променливи, записани с еднакви степени. Различават се само по коефициентите си.
2.1. Примери за подобни едночлени:
- 2x2y и −5x2y
- x3y и 7x3y7
Неподобни едночлени:
- x2y и x3y (различна степен на x)
- xy и xy2
Два подобни едночлени наричаме противоположни, ако коефициентите им са противоположни числа.
Например 2x и — 2x са противоположни едночлени.
3. Как събираме и изваждаме подобни едночлени?

Когато събираме или изваждаме подобни едночлени, събираме (или изваждаме) само техните коефициенти, а частта с променливите остава същата.
✅ Пример 1:
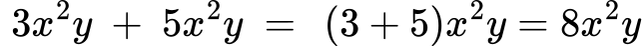
✅ Пример 2:
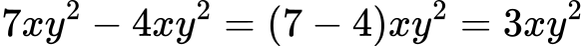
⚠️ Важно: Ако едночлените не са подобни, не можем да ги събираме или изваждаме!
Пример: 3x2y + 2xy2→ НЕ са подобни → НЕ можем да ги съберем
Сборът на противоположните едночлени е равен на 0.
Пример: 2x + ( —2x) = (2+(—-2))x = (2—2)x = 0x = 0
4. Малко по-сложен пример с повече едночлени: 🧠
Пример 3:
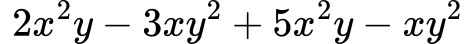
Групираме подобните едночлени:
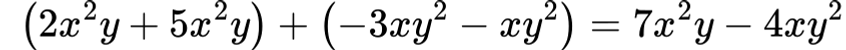
5. Обобщение: 🎯
| Понятие | Обяснение |
|---|---|
| Едночлен | Израз от числa и букви, които се умножават |
| Коефициент | Числовата част на едночлена |
| Подобни едночлени | Имат еднакви части с променливи и техните степени |
| Събиране и изваждане | Събираме или изваждаме само коефициентите |
6. Примерни задачи с решения: ✍️
🔹 Задача 1:
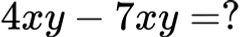
Решение:
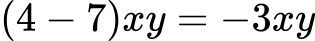
🔹 Задача 2:
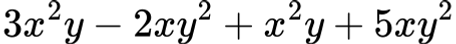
Решение:
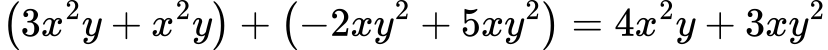
🔹 Задача 3:
Посочи кои от следните двойки са подобни едночлени:
а) 2x2y и −5x2y ✔
б) 3xy и 3xy2 ✘
в) x3y и 7x3y ✔
7. Заключение
Вече знаеш, че не всички едночлени могат да се събират, но подобните – могат, при това доста лесно! Ако помниш, че променливите трябва да съвпадат, а само числата да се смятат – значи си победител в тази малка алгебрична битка! 🧠📚
Продължавай да се упражняваш и ще станеш майстор на едночлените!