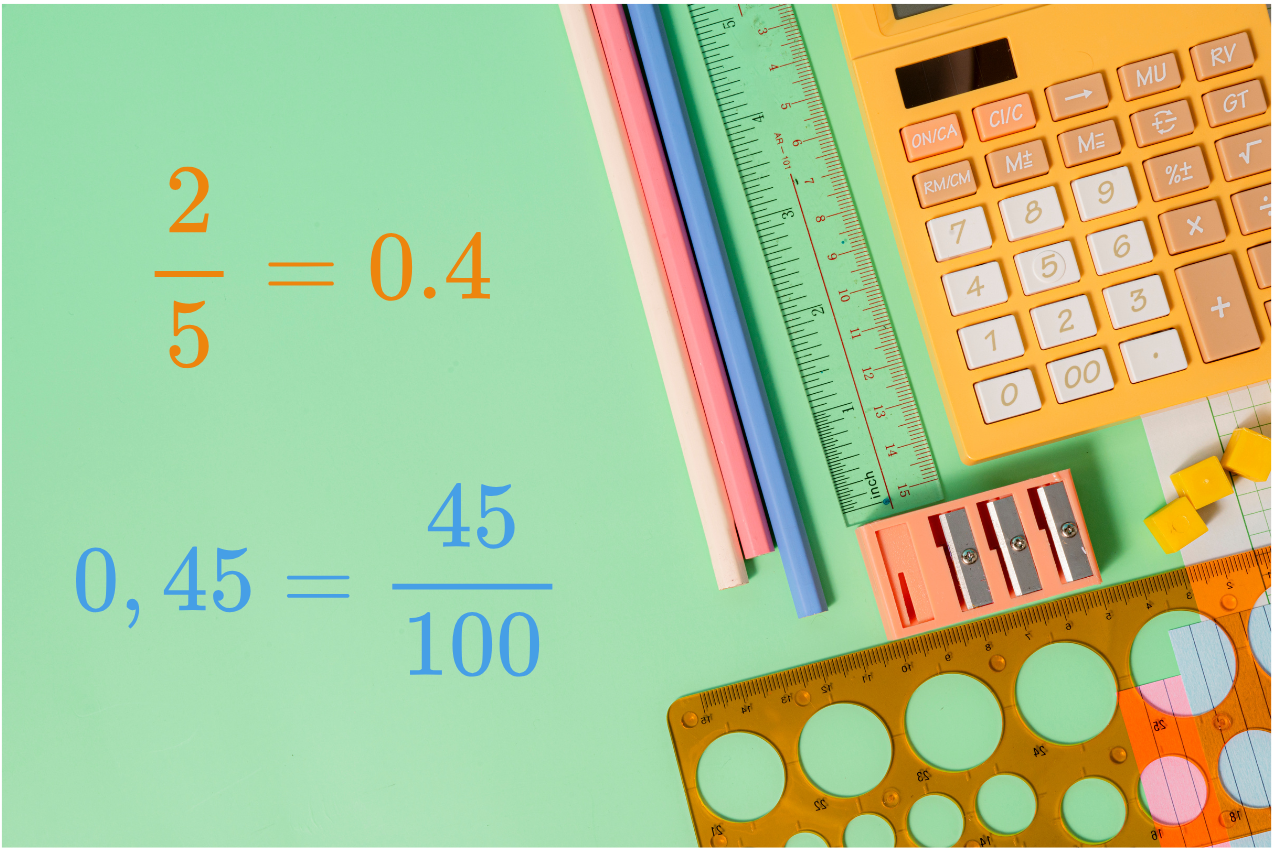Превръщане на десетични дроби в обикновени и на обикновени дроби в десетични

Здравейте, малки математици! Готови ли сте да се потопите в света на дробите? Днес ще разгледаме нещо вълнуващо – превръщане на десетични дроби в обикновени и на обикновени дроби в десетични. Това умение е като да имаш магическа пръчка – можеш да преобразуваш дробите по различни начини! Ще научите лесни трикове и ще видите как дробите се превръщат в числа, които вече познавате добре. Да започваме приключението в света на математиката!

1. Теоретична част

1.1. Превръщане на обикновени дроби в десетични

Казваме, че превръщаме една обикновена дроб в десетична, когато запишем дробното число вместо с обикновена с десетична дроб.

За да превърнем обикновена дроб в десетична, трябва да разделим числителя на знаменателя. Това означава да разделим числото отгоре на обикновената дроб на числото отдолу.

Пример:

Да превърнем следната обикновена дроб в десетична:

Така 3/4​ е равно на 0,75 като десетична дроб.

Ако след разделянето получим число, което не може да се раздели напълно, ще получим периодична десетична дроб.

Цифра или група от цифри, които се повтарят, наричаме период. Например, числата 1,333… и 2,8181… се наричат безкрайни периодични десетични дроби. Четем ги по следния начин: “едно цяло и три в период” и “две цяло и осемдесет и едно в период”.

Пример:

Тук десетичната дроб е периодична, защото числото 3 се повтаря безкрайно.

1.2. Превръщане на десетични дроби в обикновени

За да превърнем десетична дроб в обикновена, първо трябва да изразим десетичната дроб като дроб със знаменател, равен на степен 10 (например 10, 100, 1000 и т.н.). След това, ако е възможно, опростяваме дробта.

Ако една десетична дроб има краен брой цифри в дробната част, то тя може да да се нарече крайна десетична дроб. Такива дроби са например: 0,2; 1,5; 3,725 и др.

Пример 1:

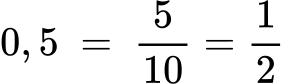
Тук дробта 5/10 се опростява (съкращава) до 1/2.

Пример 2:

Тук дробта 75/100​ се опростява (съкращава) до 3/4​.

При превръщане на периодични десетични дроби в обикновени се използват специални методи, които обаче няма да разглеждаме сега.

2. Изчислителни задачи

1. Превърнете в десетични дроби:
   • 5/8
   • Решение: 5 : 8 = 0,625
   • 2/5
   • Решение: 2 : 5 = 0,4
   • 7/10
   • Решение: 7 : 10 = 0,7
2. Превърнете в обикновени дроби:
   • 0,25
   • Решение: 0,25 = 25/100 = 1/4
   • 0,6
   • Решение: 0,6 = 6/10 = 3/5
   • 0,125
   • Решение: 0,125 = 125/1000 = 1/8
3. Превърнете в опростена обикновена дроб:
   • 0,75
   • Решение: 0,75 = 75/100 = 3/4
   • 0,45
   • Решение: 0,45 = 45/100 = 9/20
   • 0,20
   • Решение: 0,20 = 20/100 = 1/5

3. Текстови задачи

Задача 1: Един магазин продава нови играчки. През първия ден продава 2/5 от наличните 100 играчки. Колко играчки са продадени през първия ден, и колко играчки остават в магазина?

Отговор: 40 играчки са продадени, 60 играчки остават.

Задача 2: В училищната библиотека 75% от книгите са на български език, а останалите на чужд език. Ако общият брой книги е 400, колко книги са на български език и колко на чужд?

Отговор: 300 книги са на български език, а 100 на чужд език.

Задача 3: Учител дава на учениците да решат 3/4​ от 24 задачи по математика. Колко задачи трябва да решат учениците?

Отговор: Учениците трябва да решат 18 задачи.

4. Практически задачи

Задача 1: В спортен клуб тренират 120 деца. 40% от тях тренират футбол, а останалите плуване. Колко деца тренират футбол и колко тренират плуване?

Отговор: 48 деца тренират футбол, а 72 деца тренират плуване.

Задача 2: Във фирма от 200 служители 30% са инженери. Колко служители са инженери и колко служители са от други професии?

Отговор: 60 служители са инженери, а 140 са от други професии.

Задача 3: В клас от 25 ученици, 40% получават стипендия. Колко ученици получават стипендия и колко не получават?

Отговор: 10 ученици получават стипендия, а 15 не получават.

5. Заключение

Е, видяхте ли колко забавно може да бъде да превръщате дроби? Сега вече сте истински дробни магьосници!

Превръщането на обикновени дроби в десетични и обратно не е никак трудно, когато знаеш правилата. Следващия път, когато ви се наложи да решавате задачи с дроби, ще се справите като истински професионалисти! Продължавайте да се упражнявате и не забравяйте – математиката може да бъде забавна, стига да откриете вълшебните ѝ тайни!