Питагорова теорема

Здравейте, шестокласници! Днес ще се запознаем с една от най-важните теореми в математиката — Питагорова теорема! Ще научим някои факти за нейния откривател — Питагор, както и защо ни е толкова полезна в задачи с правоъгълен триъгълник.

Кой е Питагор?

Питагор е един от най-известните древногръцки философи и математици. Той е роден около 570 г. пр.Хр. на остров Самос и се е развивал в много области освен философията и математикaта — в музиката, литературата и спорта например (участвал е дори на Олимпийски игри). Питагор създава своя школа и всички негови ученици посвещавали живота си на знанието за света, закономерностите в природата и обясненията им с помощта на математически закони. На неговата школа дължим развитието на математиката и астрономията през следващите векове.

Питагорова теорема

Според една от теориите Питагор не е откривател на тази теорема, а е предал знанието за нея на древните гърци. Има данни за зависимостите в теоремата още в древен Вавилон, хиляда години преди него. Всъщност теорема наричаме доказано твърдение, което можем да използваме при решаването за задачи.

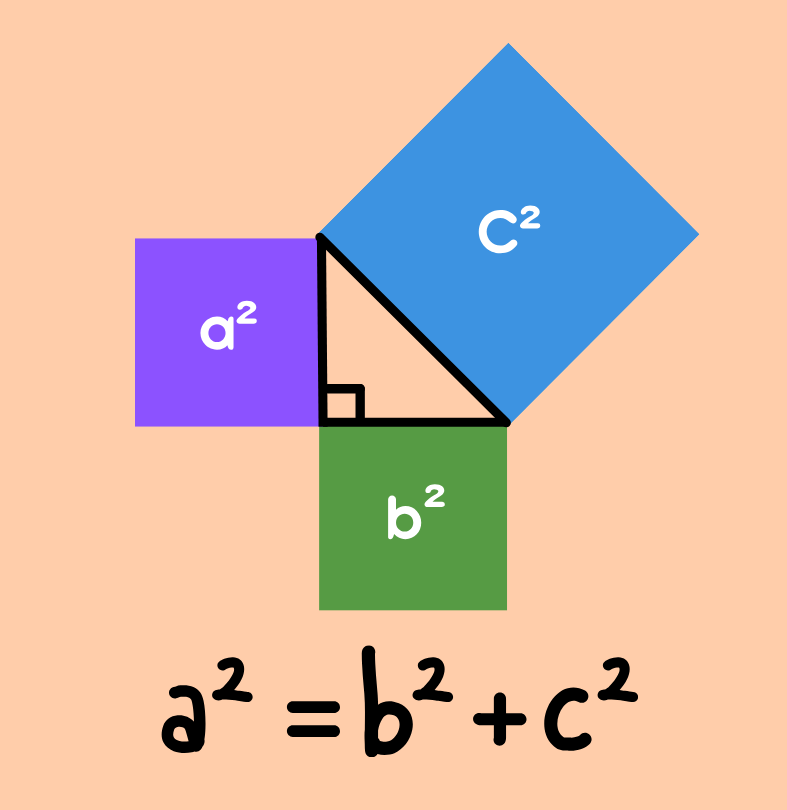
Питагоровата теорема дава връзката между страните на всеки правоъгълен триъгълник!

Тя ни позволява, ако знаем дължините на две от страните, да намерим третата страна.

Теоремата има много голямо математическо, но и практическо приложение. На това се дължат и всичките над 370 доказателства за нея.

Най—известното доказателство е с квадрати:

Ако построим квадрати, долепени до всяка от страните на правоъгълен триъгълник, лицето на квадрата,залепен за хипотенузата, е сбор от лицата на другите два квадрата.

Накратко: Сборът от квадратите на двата катета на правоъгълен триъгълник е равен на квадратът на хипотенузата му: a² + b² = c²

Питагорова тройка числа

Ако и трите страни на един правоъгълен триъгълник са естествени числа, е прието те да се наричат питагорова тройка числа. Ето едни от най — използваните питагорови тройки, които ще е много полезно да научиш наизуст:

3, 4 и 5

6, 8 и 10

5, 12 и 13

9, 12 и 15

Първите две числа са дължини на катетите, а третата — на хипотенузата (най-дългата му страна). Питагоровите тройки се използват освен за бързо приложение на теоремата в задачи, но и за построяване и разпознаване на прав ъгъл.

В древността са използвали питагорова тройка числа, за да построяват прав ъгъл с помощта на въже. Тогава не е имало модерни инструменти и хората са използвали близки до ежедневието им предмети.

Геометрична задача с питагорова теорема

Да видим сега как на практика се прилага тази теорема със следващата задача:

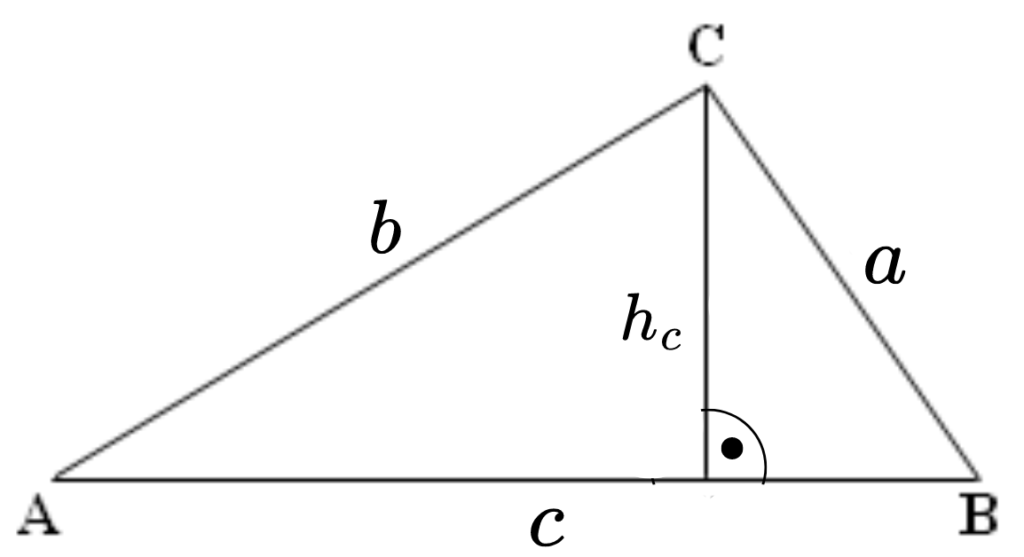
Правоъгълен триъгълник има дължина на единия катет 8 cm, а най-дългата му страна е 17 cm. Намерете дължината на другия му катет и височината към хипотенузата му.

Това е една основна геометрична задача, може би ти е позната!

За да намерим другият катет, трябва да използваме питагоровата теорема, а за да изчислим височината към хипотенузата на правоъгълния триъгълник, трябва да се сетим, че има два начина да пресметнем неговото лице — като използваме катетите или като използваме хипотенузата и височината към нея.

А сега да опишем задачата!

Дадено:

a = 8 cm

c = 17 cm

b = ?

h_c = ?

Решение:

a² + b² = c²

8²+ b² = 17²

64 + b² = 289

b² = 289 —64

b² = 225

b = 15 cm

Дължината на катета е положително число, затова b = —15 не е решение.

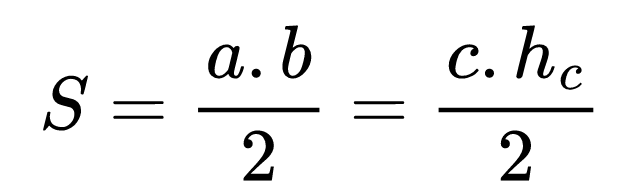
Не е нужно да намираме лицето на триъгълника, тъй като не искат това от нас в задачата. Използваме обаче равенството, за да получим зависимостта:

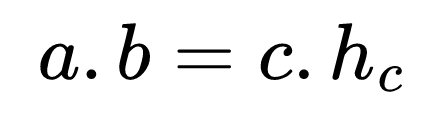
8.15 = 17 . h_c

120 = 17 .h_c

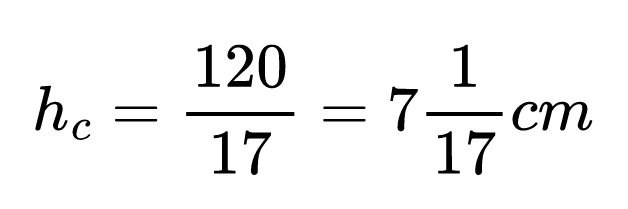
Практическа задача с питагорова теорема

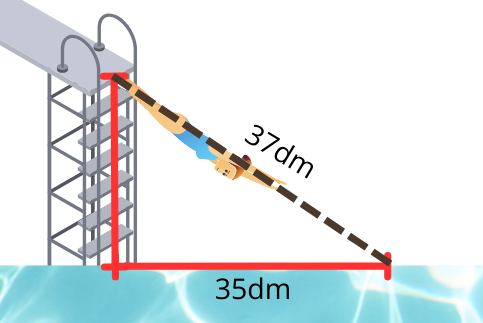
Състезателка по скокове във вода скача от трамплин. Разстоянието, което тя изминава от трамплина до водната повърхност 37 dm. Намерете дължината на трамплина над водата, ако разстоянието от него до точката на гмуркане е 35 dm.

Решение:

Трамплинът сключва прав ъгъл с водната повърхност и от чертежа се вижда правоъгълния триъгълник, който получаваме при скока на състезателката. Имаме дължината на единия катет и дължината на неговата хипотенуза. За да намерим другият катет, прилагаме питагорова теорема.

Дадено:

a = 35 dm

c = 37 dm

b = ?

Решение:

a² + b² = c²

35² + b² = 37²

1225 + b² = 1369

b² = 1369 — 1225

b² = 144

b = 14 dm

В нашата задача катетът е дължина на трамплина над водата, затова може да е само положително число, b = —14 не е решение.