Многочлен. Нормален вид на многочлен.

Здравей, малък изследователю на математиката! Представи си, че си архитект и строиш изрази от “тухлички”, наречени едночлени. А когато събереш няколко такива тухлички – получаваш многочлен! Точно както сграда е съставена от много части, така и многочленът е съставен от едночлени.

В тази статия ще ти покажем:

• какво е многочлен
• как изглежда в нормален вид
• как да работиш с многочлени лесно и уверено.
  Да започваме!

1. Какво е многочлен?

Многочлен е алгебричен израз, който се състои от сбор или разлика на два или повече едночлена.

Алгебричният сбор на едночлени наричаме още многочлен (полином). Едночленът също е многочлен.

🔹 Примери за многочлени:

• 3x + 2
• 2x²y − xy + 4
• x² − 5x + 6

➡ Всеки отделен член (като 3x, −xy, 4) е едночлен, а всички заедно – многочлен.

2. Как изглежда многочлен в нормален вид?

Казваме, че един многолен е в нормален вид, ако всички едночлени в него са в нормален вид и няма подобни едночлени.

Многочленът е в нормален вид, когато:

1. Всички подобни едночлени са събрани
2. Подреден е по степен (обикновено в низходящ ред)
3. Всеки член е написан в нормален вид (като едночлен)

2.1. Коефициенти на многочлен

Коефициентите на членовете на даден многочлен в нормален вид се наричат коефициенти на многочлена.

✅ Пример 1:

Mногочленът:

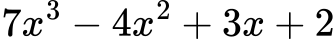
е сбор от едночлените:

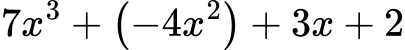
и има коефициенти: 7; -4; 3 и 2; където 2 е коефициент в едночлена 2x⁰ = 2 . 1 = 2 и се нарича свободен член.

2.2. Степен на многочлен

Най-високата степен на членовете в нормален вид на един многочлен, наричаме степен на многочлена.

✅ Пример 2:

Mногочленът:

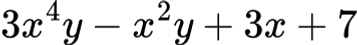
е от пета степен, защото 3x⁴y е членът с най-висока степен (4 + 1 = 5).

✅ Пример 3:

Многочленът:

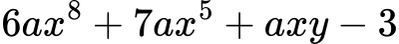
е от осма степен, защото 6ax⁸ е членът с най-висока степен (8-ма).

2.3. Приведете в нормален вид многочлените:

✅ Пример 4:

Даден е изразът:

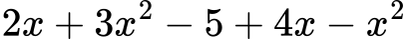
Стъпка 1: Групираме подобните едночлени:

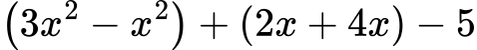
Стъпка 2: Изчисляваме:

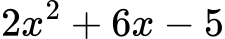
➡ Това е нормалният вид на многочлена.

✅ Пример 5:

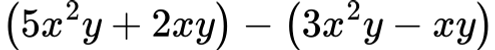
Първо премахваме скобите:

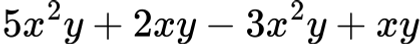
Групираме подобните:

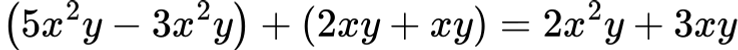
➡ Нормален вид: 2x²y+3xy

3. Какво включва многочленът?

Част на многочлена	Обяснение
Членове	Отделните едночлени, които го съставят
Коефициент	Числото пред променливите във всеки член
Степен на члена	Сумата от степените на променливите в този член
Степен на многочлена	Най-голямата степен от всички членове

🧪 Пример 6:

Да разгледаме:

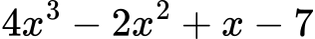
• Членове: 4x³, −2x², x, −7
• Коефициенти: 4, -2, 1, -7
• Степени на членовете: 3, 2, 1, 0
• Степен на многочлена: 3 (най-голямата)

4. Упражнителни задачи с решения: ✍️

🔹 Задача 1:

Приведи в нормален вид:

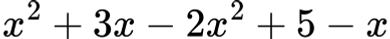
Решение:

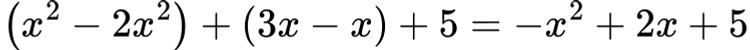
🔹 Задача 2:

Намери степента на многочлена:

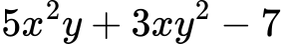
Решение:

• x²y → степен: 3
• xy² → степен: 3
• −7 → степен: 0
  ➡ Степен на многочлена: 3

🔹 Задача 3:

Групирай подобните членове и запиши в нормален вид:

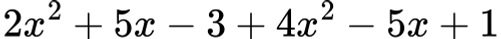
Решение:

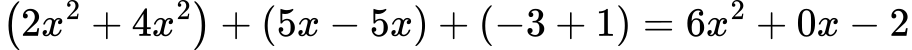
➡ Нормален вид: 6x² − 2

5. Заключение

Вече знаеш, че многочленът не е нещо страшно, а просто сбор или разлика на едночлени!
Когато събираш подобните и подредиш правилно израза – той се превръща в нормален вид, точно както строител подрежда тухлите по план. 🧱

След още няколко упражнения, ще можеш да боравиш с многочлени като истински математик! 🧠💪