Лице на повърхнина на права призма

Здравейте, шестокласници! Време е да преминем на следващото ниво с уроците за права призма!Днес ще се научим да решаваме задачи с лице на околна повърхнина и лице на повърхнина на права призма.

Лице на околна повърхнина на права призма

В пети клас вече сте учили как се намира лице на околна повърхнина и лице на повърхнина на куб и правоъгълен паралелепипед. Те са прави призми, затова знанията за тези две тела ще са ни много полезни.

Да разгледаме първо една права триъгълна призма и нейната развивка.

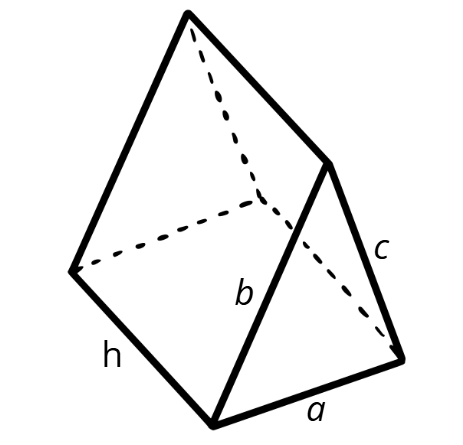
Основите на тази призма са два еднакви триъгълника, а стените са правоъгълници. Ако срежем призмата по ръбовете и я разпънем, ще получим ето тази развивка:

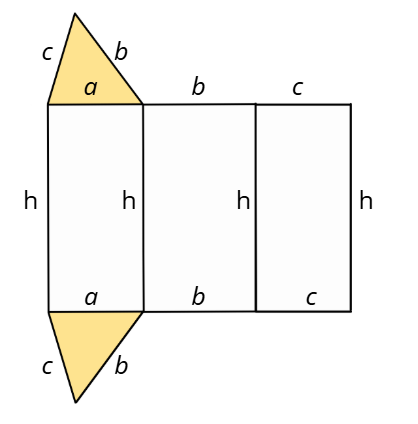
Околната повърхнина на призмата е сбор от лицата на околните ѝ стени.

Трите околни стени са правоъгълници, на които единият размер е височината на призмата, а другият — основен ръб на призмата:

S = a . h + b . h + c . h = ( a + b + c ) . h = P . h

Лицето на околната повърхнина на права призма е равно на произведението от периметъра на основата и височината на призмата.

S = P . h

Лице на повърхнина на права призма

Често в задачите вместо “лице на пълна повърхнина” ще срещате понятието “лице на повърхнина”. Просто думичката “пълна” се пропуска. За вас е важно да запомните, че ако не е записано околна повърхнина, то със сигурност повърхнината е пълна.

Разликата между пълната и околната повърхнина е, че пълната повърхнина е равна на сбора от лицата на всички стени на призмата. Тогава към околната повърхнина трябва да добавим и двете основи.

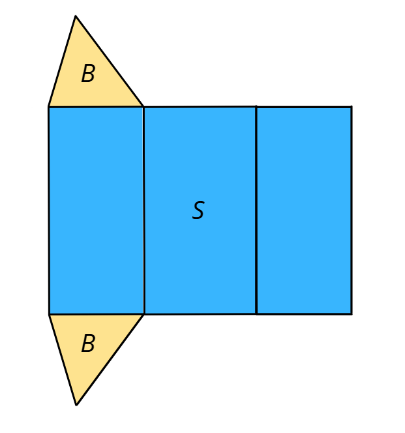
От пети клас знаем, че има специална буква за означаване на лице на основата на геометрично тяло — B. Основите в случая са два еднакви многоъгълника, така че е достатъчно към лицето на околната повърхнина на добавим удвоеното лице на едната основа:

S₁ = S + 2 . B

Ако запомните, че всяка от повърхнините е сбор от лица на стени, ще можете самички да си изведете формулите, дори да сте ги забравили! Това е много ценно, тъй като изучените тела стават все повече, а с тях се увеличава и броят на формулите за намиране на техните повърхнини и обеми.

Основни задачи с лице на околна повърхнина на права призма

Задача №1

Намерете лицето на околната повърхнина на правилна триъгълна призма с основен ръб 4 dm и околен ръб 80 cm.

Дадено:

b = 4 dm

h = 80 cm = 8 dm

S = ?

Решение:

Височината на призмата е равна на дължината на околния ръб.

Важно е в началото да запишете дължините в една и съща мерна единица. В някои задачи още в условието е посочено в каква мерна единица да запишете полученото лице, но в случая не е така.

Призмата е правилна триъгълна, затова е основата ѝ е равностранен триъгълник.

P = 3 . b

P = 3 . 4 = 12 dm

S = P . h

S = 12 . 8 = 96 dm²

Задача №2

Околната повърхнина на права четириъгълна призма с основа равнобедрен трапец е 1200 cm² . Намерете бедрото на трапеца, ако височината на призмата е 2 dm, малката основа на трапеца е 8 сm, a голямата му основа е с 50% по-голяма от нея.

Дадено:

S = 1200 cm²

h = 2 dm = 20 cm

b = 8 cm

a = 150%.b

c = d = ?

Да видим как изглеждат призмата и нейните основи:

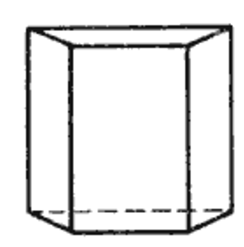
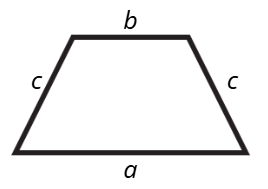
Решение:

Първо намираме периметъра на основата от формулата за околна повърхнина на призма.

S = P . h

1200 = P . 20

P = 60 cm

Използваме формулата за обиколка на равнобедрен трапец:

P = a + b + 2 . c

60 = 150%. b + b + 2 . c

60 = 1,5 . 8 + 8 + 2 . c

60 = 12 + 8 + 2 . c

2 . c = 60 — 20

c = 40 / 2

c = 20 cm

Основни задачи с лице на повърхнина на права призма

Задача №1

Намерете дължината на основния ръб на правилна четириъгълна призма, ако околната ѝ повърхнина е 288 m², a лицето на повърхнината на призмата е е 360 m².

Дадено:

S = 288 m²

S₁ = 360 m²

b = ?

Решение:

Използваме формулата за повърхнина на призма:

S₁ = S + 2 . B

360 = 288 + 2 . B

2 . B = 360 — 288

2 . B = 72

B = 72 / 2 = 36 m²

Основата на правилна четириъгълна призма е квадрат, затова:

B = b . b

36 = b . b

b = 6 m

Задача №2

По данните от чертежа намерете лицето на повърхнината на правилната шестоъгълна призма.

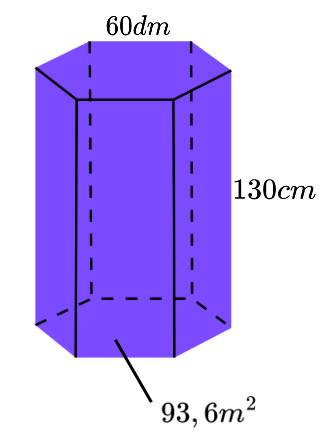
Дадено:

B = 93,6 m²

h = 130 cm = 1,3 m

b = 60 dm = 6 m

S₁ = ?

Решение:

S₁ = S + 2 . B

S = P . h

S = 6 . b . h

S = 6 . 6 . 1,3

S = 46,8 m²

S₁ = 46,8 + 2 . 93,6

S₁ = 46,8 + 187,2

S₁ = 234 m²

Практическа задача с лице на повърхнина на права призма

Изгледайте следващото видео, за да се запознаете с една много интересна практическа задача!

А сега е време да се упражните със следващия тест!