Задачи от движение

Здравейте, седмокласници! Време е да изучим в по-голяма дълбочина задачи от движение. Вярвам, че голяма част от вас са наясно с връзката между величините скорост, път и време. Сега ще се запознаем с алгоритмите за решаване на този вид задачи, като разгледаме случаите, в които превозните средства се движат в една и съща посока и в противоположни посоки.

Основни стъпки при решаване на задачи от движение

Ако сте забравили алгоритъма при решаване на текстови задачи, може да си го припомните ето тук:: Моделиране с уравнения

Нека припомним основната формула, която ще ни е нужна днес:

Важно е да си представим самата задача, за което много помага да си начертаем схема на движението.

За удобство този вид задачи се структурират в таблица. В нея се подрежда информацията от условието на задачата, като се изразяват и зависимостите между величините. Много важен момент е след избора на неизвестното да зададете допустими стойности за него.

След попълването на таблицата трябва да съставим уравнение и да го решим. Най-често уравнението се съставя за изминатия път. След получаването на отговора трябва да проверим дали той отговаря на допустимите стойности.

Задача, в която превозните средства се движат в една и съща посока.

Да решим следната задача.

Лека кола и автобус тръгват едновременно в 10 часа от град А в посока град B. Леката кола се движи с 90 km/h, а автобусът – със скорост, която е с 1/9 по-ниска от тази на леката кола. В колко часа леката кола ще се намира на 5 km пред автобуса?

Решение:

Нека първо изчислим скоростта на автобуса. Тя е с 1/9 по-ниска, затова:

V_{автобус} = V_{лека кола} — (1/9).V_{лека кола}

V_{автобус} = 90 — (1/9).90 = 90 — 10 = 80 km/h

Можем да онагледим решението със следната схема:

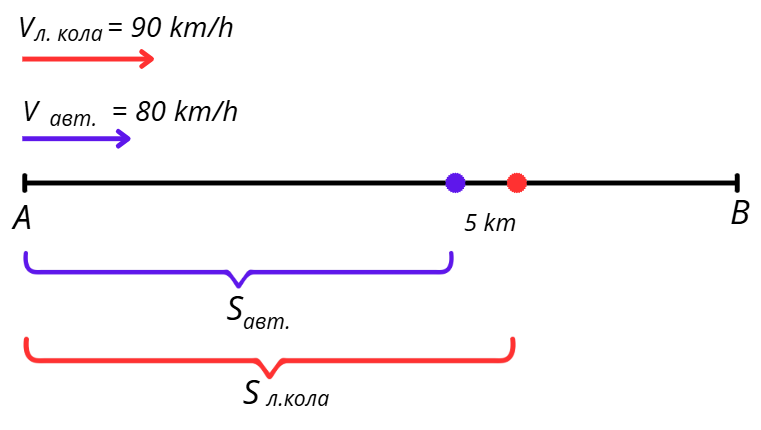
Можем да съставим таблицата, която да обобщи основната информация. Нека неизвестното бъде времето, за което са се движили двете превозни средства. Тъй като те тръгват едновременно от град А, то ще е едно и също за двете превозни средства.

Превозно средство	V (km/h)	t (h)	S = V.t (km)
Лека кола	90 km/h	x	90x
Автобус	80 km/h	x	80x

Времето за движение трябва да е положително число, затова въвеждаме допустими стойности за неизвестното.

Допустими стойности за x > 0 ( ДС: x > 0)

Въпросът е в колко часа леката кола ще е на 5 km пред автобуса. В този момент тя ще е изминала 5 km повече от автобуса. Съставяме уравнението:

S_{лека кола} — S_{автобус} = 5 km

90x — 80x = 5

10x = 5

x = 5/10

x = 1/2 h

Полученият отговор е от допустимите стойности на неизвестното, тъй като 1/2 > 0.

Следователно след половин час, или 30 минути, разстоянието между двете превозни средства ще е 5 km. Тъй като те са тръгнали заедно в 10:00 часа от град А, това ще се случи в 10:30 часа.

Задачи, в които превозните средства се движат едно срещу друго

Нека разгледаме следващия тип задачи, в които превозните средства се движат едно срещу друго.

В 9:00 часа сутринта от град A към град B тръгнал велосипедист, който се движи с 15 km/h. В 9:20 часа от град B към град А тръгнал мотоциклетист, който се движил със скорост, с 400% по-висока от тази на велосипедиста. Намерете в колко часа двете превозни средства ще се срещнат, ако разстоянието между двата града е 155 km.

Решение:

Нека първо пресметнем скоростта на мотоциклетиста.

V_{мотоциклитист} = V_{велосипедист} + 400%.V_{велосипедист}

V_{велосипедист} = 15 + 400%.15 = 15 + 4.15 = 5.15 = 75 km/h

Друг важен момент е да запишем минутите в часове.

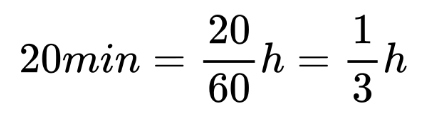
Нека разгледаме схемата на движението.

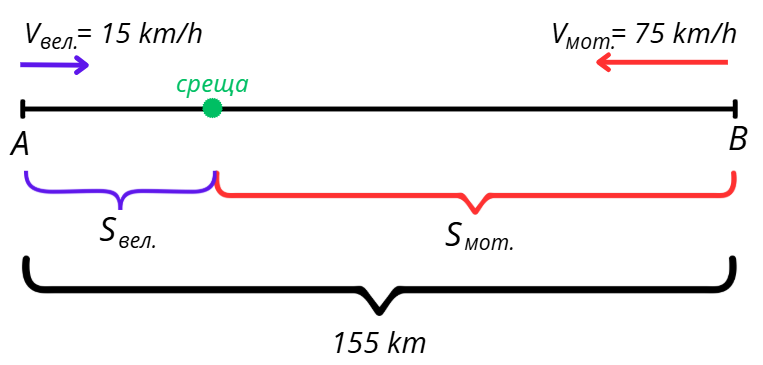
А сега да запишем данните в таблицата. Тук неизвестно може да е както времето за движение на велосипедиста, така и времето за движение на мотоциклетиста. Няма значение за крайния отговор какво ще изберете.

Превозно средство	V (km/h)	t (h)	S = V.t (km)
Велосипедист	15 km/h	x	15x
Мотоциклетист	75 km/h	x — 1/3	75(x — 1/3)

Допустимите стойности за неизвестното са времената и на двете превозни средства да са положителни числа, т.е. x > 0 и x > 1/3.

От тук следва, че ДС: x > 1/3

За съставянето на уравнението е достатъчно да съобразим, че разстоянието между двете населени места е 155 km, затова сборът от пътищата на двете превозни средства ще е равен на 155 km.

S_{велосипедист} + S_{мотоциклетист} = 155 km

15x +75(x — 1/3) = 155

15x +75x — 25 = 155

90x = 155+25

90x = 180

x = 2h

Проверката показва, че получената стойност за неизвестното (x=2) отговаря на допустимите стойности, тъй като 2 > 1/3.

Двете превозни средства ще се срещнат след 2 часа от тръгването на велосипедиста (който е тръгнал в 9:00 ч.), т.е. в 11:00 часа.

Обобщение

• Начертайте схема, която ще онагледи задачата и ще ви помогне при нейното решение.
• Съставете таблица, която ще съдържа информацията за скорост, път и време.
• Задайте допустими стойности на неизвестното.
• Съставете и решете уравнението.
• Проверете дали получената стойност за неизвестното попада в допустимите стойности.
• Отговорете на въпроса в задачата.

Време е да приложите алгоритъма, за да решите задачите в теста.