Задачи от движение. Задачи с движение по река.
Привет, седмокласници! Днес ще решаваме отново задачи от движение, но този път по-специфични – задачи с движение по река с лодка, сал, кораб или друг плавателен съд. Ще видите, че тези задачи са лесни и логични!
Основни зависимости при движение по река
ри решаването на задачи с движение по река използваме основната зависимост между скорост (V), време (t) и изминат път (S): S = V .t.
Особеността тук е влиянието на скоростта на течението (Vтеч) върху собствената скорост (Vсоб.ск.) на плавателния съд.

Когато плавателен съд се движи по течението на реката, тя увеличава скоростта му със скоростта на течението.
Когато имаме движение срещу течението на реката, скоростта се намалява със скоростта на течението.
Малко по-особени са задачите, в които се движи сал, тъй като той се движи със скоростта на течението.
| Посока на движение | Формула за скоростта (V) |
| По течението | Vпо теч. = Vсоб.ск + Vтеч |
| Срещу течението | Vсрещу теч. = Vсоб.ск – Vтеч |
| Движение на сал | Vсал = Vтеч |
Останалата част от алгоритъма за решение е същата: избираме неизвестно, определяме допустимите му стойности, попълваме таблица, съставяме и решаваме уравнение.
Задача с движение по река, в която неизвестна е собствената скорост на лодката
Лодка изминава разстоянието между две пристанища, като се движи 6 часа по течението и 8 часа срещу течението на реката. Намерете разстоянието между двете пристанища, ако скоростта на течението на реката е 2 km/h.
Нека направим схема на движението. Понякога с наклон се показва посоката на движение на реката.
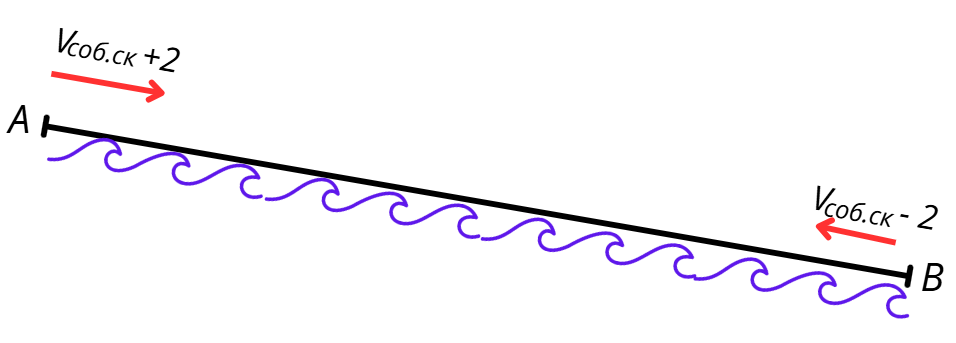
Нека попълним таблицата с информацията от условието на задачата.
| Посока на движение | V (km/h) | t (h) | S = V.t (km) |
| по течението | Vсоб.ск + 2 | 6 | (Vсоб.ск. + 2).6 |
| срещу течението | Vсоб.ск — 2 | 8 | (Vсоб.ск — 2).8 |
Изминатият път в двете посоки е един и същ. Съставяме уравнението, като неизвестно в него е собствената скорост на лодката. Тя трябва да е по-голяма от 2, за да може лодката да се движи срещу течението (Vсоб.ск >2).
(Vсоб.ск. + 2).6 = (Vсоб.ск — 2).8
6.Vсоб.ск + 12 = 8.Vсоб.ск — 16
28 = 2.Vсоб.ск
Vсоб.ск = 14 km/h
Остава да намерим разстоянието между двете пристанища, като заместим получената стойност за собствената скорост на лодката:
S = (Vсоб.ск. + 2).6 = (14 + 2) .6 = 16 . 6 = 96 km
Задача с движение по река, в която неизвестна е скоростта на течението
Лодка се движи в спокойни води с 15 km/h. Тя изминала по течението на реката 34 km за 2 часа, след което още 13 km се движела срещу течението. Намерете скоростта на течението и времето, за което лодката е изминала пътя срещу течението.
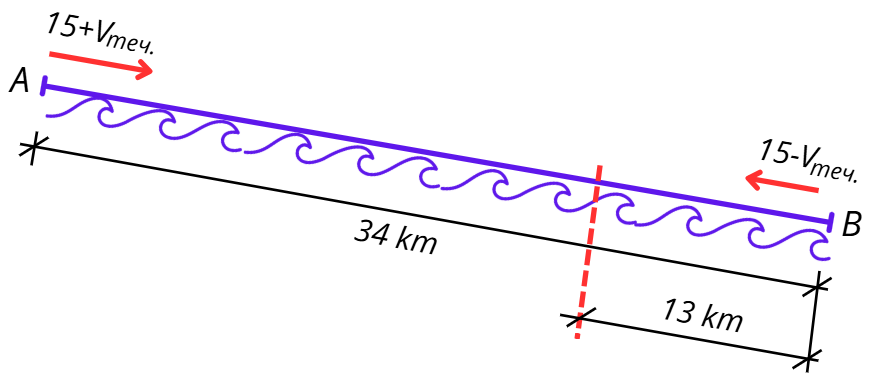
Да съставим таблицата:
| Посока на движение | V (km/h) | t (h) | S = V.t (km) |
| по течението | 15 + Vтеч | 2 | (15 + Vтеч).2 |
| срещу течението | 15 — Vтеч | x | (15 — Vтеч).x |
Времето за движение срещу течението ще означим с x.
Скоростта на движение на реката, както и времето за движение трябва да са положителни числа (Vтеч > 0; x>0)
В тази задача знаем какво е разстоянието, което лодката изминава по течението на реката и можем да съставим следното уравнение:
(15 + Vтеч).2 = 34 /:2
15 + Vтеч = 17
Vтеч = 2 km/h
Можем да пресметнем изминатия път срещу движението като заместим с вече получената скорост на течението.
(15 — 2).x = 13
13x = 13
x = 1h
Лодката се е движила един час срещу течението на реката, a скоростта на течението е 2 km/h.
Задача с движение на сал
В 9:45 часа сутринта от две пристанища едновременно един срещу друг тръгнали катер и сал. Собствената скорост на катера е 40 km/h, а скоростта на течението е 3 km/h. Двете пристанища са на 120 km едно от друго. Пресметнете в колко часа ще се срещнат.
Тук трябва да съобразим, че салът няма собствена скорост и той се движи със скоростта на течението. Със сигурност в нашата задача катерът се движи срещу течението на реката.
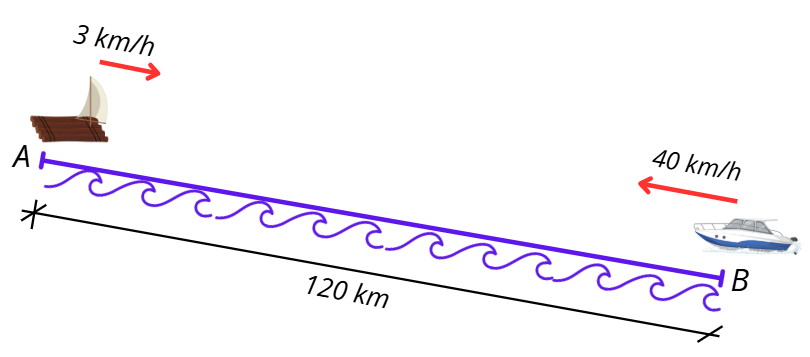
| Превозно средство | V (km/h) | t (h) | S = V.t (km) |
| катер | 40 —3 | x | 37x |
| сал | 3 | x | 3x |
Времето, за което са се движили двете превозни средства трябва да е положително число (x>0).
След като вече сме попълнили таблицата, остава да съставим уравнението. Сборът от изминатите от двете превозни средства разстояние е равен на 120 km. (Sкатер + Sсал = 120 km)
37x + 3x = 120
40x = 120
x = 120/40
x = 3h
Двете превозни средства ще се срещнат след 3 часа. Тъй като са тръгнали в 9.45, срещата ще е в 12.45ч.
Обобщение
При решаването на задачи от движение по река е от съществено значение да се определи дали плавателният съд се движи по течението или срещу течението, за да се изчисли неговата реална скорост. След това се прилагат стандартните стъпки за решаване на текстови задачи от движение.
Време е за упражнение! Решете задачите от теста!