Еквивалентни уравнения
Математиката често ни се струва като език на тайни послания. Едно уравнение може да изглежда сложно и дълго, но с правилните стъпки можем да го преобразуваме до по-просто, без да променяме неговия отговор. Това е силата на еквивалентните уравнения – различни на вид, но със същото решение.
В този урок ще научим какво е корен на уравнение, как да разпознаваме еквивалентни уравнения и как да ги използваме, за да решаваме по-лесно математически и практически задачи.
1. Теоретична част
1.1. Какво е уравнение?

Уравнение е равенство, в което участва неизвестно число (обикновено означено с буква).
Пример:
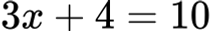
1.2. Какво е корен на уравнение?

Корен на уравнение е числото, което превръща уравнението във вярно, ако бъде заместено на мястото на неизвестното.
Пример:
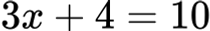
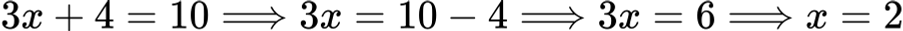
При x = 2⇒ 3 ⋅ 2 + 4 = 10
👉 Следователно x = 2 е корен.
1.3. Кога уравнения са еквивалентни?

Еквивалентни уравнения са тези, които имат едни и същи корени.
Пример: 3x + 4 = 10 ⇔ 3x = 6⇔ x = 2
Всички тези уравнения са еквивалентни, защото имат едно и също решение.
1.4. Какви преобразувания запазват еквивалентността?

- Прибавяне или изваждане на едно и също число/израз от двете страни.
- Умножение или деление на двете страни с едно и също число, различно от нула.
2. Примери с решения✅:
Пример 1
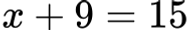
Изваждаме 9:
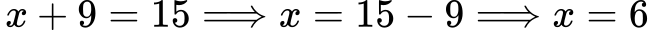
Пример 2

Прибавяме 7:
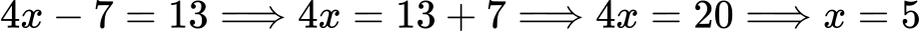
Пример 3
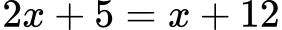
Прехвърляме x вляво и 5 вдясно:
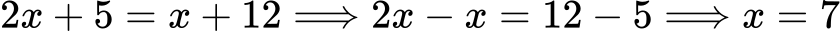
Пример 4
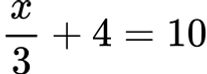
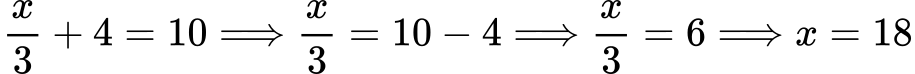
Пример 5
В училищен стол 3 еднакви сандвича и напитка струват общо 9 лв. Ако напитката струва 3 лв., колко струва един сандвич?
Решение:
Нека сандвичът струва x лв. ⇒ 3x + 3 = 9 ⇒ 3x = 6 ⇒ x = 2
👉 Един сандвич струва 2 лв.
3. Заключение
Еквивалентните уравнения ни показват, че понякога сложният път може да се съкрати. Те са ключът към това да решаваме уравнения по-бързо и сигурно. Запомнете: еквивалентните уравнения изглеждат различно, но отговарят на един и същи въпрос. Когато овладеете тези преобразувания, ще можете да намирате решения в математиката така, както откривате скрити съкровища!