Тъждеството (a+b)(a-b) = a2 – b2 сбор по разлика на два израза
В алгебрата често срещаме изрази със скоби, които изглеждат дълги и трудни за пресмятане. Но математиката има своите „съкратени пътища“ – специални формули, които ни помагат да опростяваме задачите по-бързо и лесно.
Една от тези формули е тъждеството сбор по разлика на на два израза. Тя изглежда просто, но е много полезна. Може да я срещнете в задачи за преобразуване на изрази, намиране на стойности и дори в по-сложни теми като уравнения.
1. Теоретична част

Произведението на сбора и разликата на два израза е равно на първия израз, повдигнат на квадрат, минус втория израз, отново повдигнат на квадрат.
🔹 Формула:
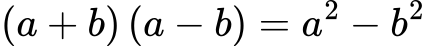
Ако означим а и b съответно с А и B, то формулата може да се запише схематично като:
(A + B)(A – B) = A2 + B2
🔹 Обяснение стъпка по стъпка
Умножаваме a по a и получаваме a2.
- Умножаваме a по +b → получаваме +a.b.
- Умножаваме −b по a → получаваме −a.b.
- Умножаваме −b по +b → получаваме −b2.
- Двете смесени произведения +a.b и −a.b се унищожават взаимно.
Остава: a2 − b2
🔹 Кога се използва?
Формулата може да се приложи, когато имаме произведение на два израза, които:
👉са в скоби и са огледални (пример: x+7 и x−7).
👉са еднакви, но се различават само по знака между тях – единият е „+“, другият „–“;
2. Примери с решения✅:
Пример 1
Приведи в нормален вид:
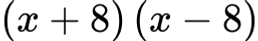
Решение:
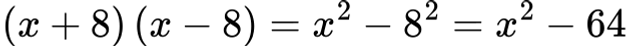
Пример 2
Приведи в нормален вид:
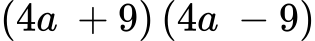
Решение:
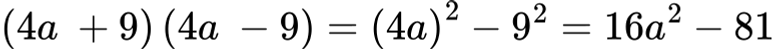
Пример 3
Намери стойността на:
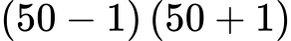
Решение:
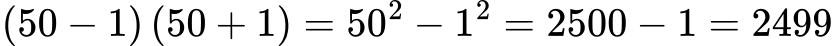
👉 Това е чудесен пример, че формулата може да ни спести време, защото вместо да умножаваме 49 по 51, използваме квадрата на 50.
Пример 4
Приведи в нормален вид:
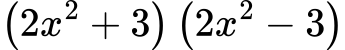
Решение:
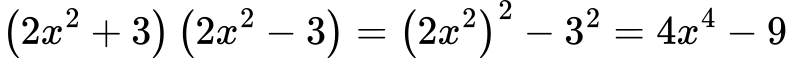
3. Приложение на формулата в реалния живот 🌍:
Може да изглежда, че „разлика на квадрати“ е само суха математика, но тя се използва:
във висшата математика – за факторизация на изрази.
в бързи изчисления (напр. за намиране на произведения на числа, близки до кръгли – 99·101, 49·51 и др.);
в алгебрични опростявания, когато решаваме уравнения;
4. Заключение
Разликата на квадрати е една от най-лесните и най-полезни формули в алгебрата. Тя показва, че математиката не винаги е дълги сметки – често има скрити „вратички“, които ни спестяват време.
Запомни формулата: (a+b)(a-b)=a2−b2
и ще имаш верен помощник във всички задачи, в които се появяват огледални изрази.