Обем на права призма
Здравейте, шестокласници! Време е за поредното ни приключение, което включва задачи с права призма. Днес ще се научим как се намира обем на права призма и какви практически задачи може да се решават с нея.

Ако имате нужда да си припомните кое обемно тяло наричаме права призма и как се намират неговите повърхнини, прочетете ето тези статии:
Обем на права призма
Обемът на права призма се намира много лесно! Достатъчно е да изчислим лицето на основата и да го умножим по височината на правата призма. Това е знание, което имате още от 5. клас, тъй като тогава сте изучили обемите на две тела, които са прави призми-правоъгълен паралелепипед и куб.

Обемът на права призма е равен на произведението от лицето на основата и неговата височина.
V = B . h
Трябва да сме внимателни с вида на призмата, за да определим вярно каква е основата му. Тъй като основите може да са всякакъв вид многоъгълници, тук използваме различни формули за намиране на тяхното лице. Много е важно да ги знаете безгрешно и да не губите време, за да ги търсите.
Основни задачи с обем на права призма
Задача №1
Височината на права четириъгълна призма с основа успоредник е 3 пъти по-дълга от основния ѝ ръб. Намерете обема на призмата, ако височината на успоредника е равна на 10 dm и е с 25% по-дълга от страната на успоредника.
Дадено:
h = 3 . b
hусп= 10 dm
125% . b =10 dm.
V = ?
Решение:
Първо намираме основния ръб на призмата:
1,25 . b = 10
b = 10 : 1,25
b = 8 dm
Сега намираме лицето на основата:
B = b . hусп
B = 8 . 10 = 80 dm2
Остава да пресметнем височината на призмата и нейния обем.
h = 3 . b
h = 3 . 8 = 24 dm
V = B . h
V = 80 . 24
V = 1920 dm3
Задача №2
Намерете височината на правилна шестоъгълна призма с обем 655,2 cm3, ако апотемата на основата е 5,2 cm, а основният ръб на призмата е 6 cm.
Дадено:
V = 655,2 cm3
a = 5,2 cm
b = 6 cm
h = ?
Решение:
Намираме лицето на основата, която е правилен шестоъгълник.
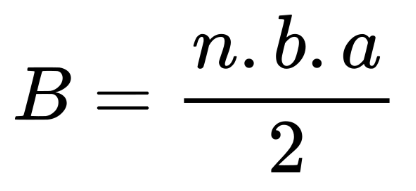
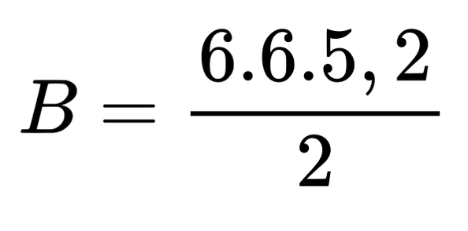
B = 93,6 cm2
Остава да изчислим височината на призмата като използваме формулата за обем.
V = B . h
655,2 = 93,6 . h
h = 655,2 : 93,6
h = 7 cm
Практически задачи с обем на аквариум
Пресметнете колко литра вода побира аквариума по зададените от чертежа размери:
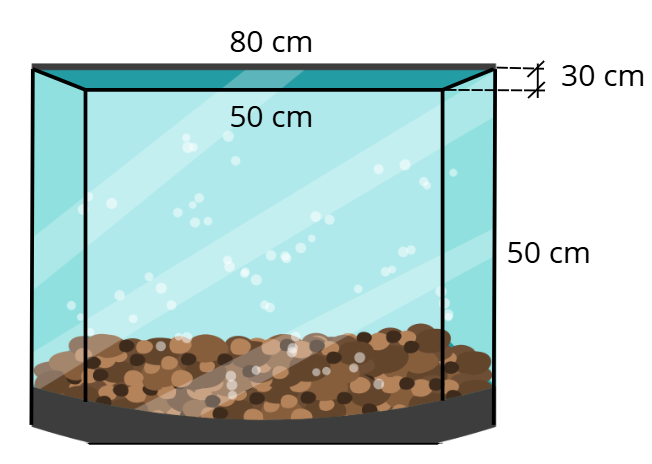
Дадено:
h = 50 cm
a = 80 cm
b = 50 cm
hтрапец = 30 cm
V = ?
Решение:
Основата на аквариума е трапец. Намираме лицето му:
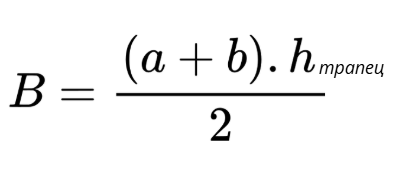
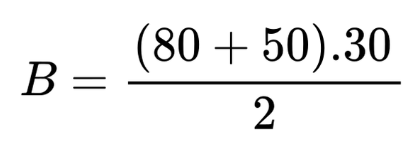
B = 1950 cm2
Остава да намерим обема на аквариума и да го запишем в литри.
V = B . h
V = 1950 . 50
V = 97500 cm3 = 97,5 dm3 = 97,5 l
Аквариумът побира 97,5 l вода. Ако трябва да го закръглим с точност до единиците, това са 98 l.
Практическа задача с хладилник
Намерете височината на хладилника, ако знаете, че заема 0,720 m3 и основата му е правилен четириъгълник със страна 60 cm.
Дадено:
b = 60 cm
V = 0,720 m3 = 720 dm3 = 720 000 cm3
h = ?
Решение:
Хладилникът има форма на права призма с основа квадрат. Намираме първо лицето на основата:
B = b . b
B = 60 . 60 = 3600 cm2
Сега използваме формулата за обем на призма, за да изчислим височината.
V = B . h
720 000 = 3600 . h
h = 720 000 : 3600
h = 200 cm
Получихме, че хладилникът е висок 2 m.
Задача с обемно тяло, съставено от две призми
Изгледайте следващото видео, за да видите как можем да намираме обем на тяло, което е съставено от повече от една призма.

Време е да се упражните със следващия тест!