Множества. Кръгове на Ойлер
Здравейте, приятели от 6.клас! Новите знания в тази статия са много интересни и полезни, а задачите в тях се срещат и на математически състезания. Със сигурност е важно да научите какво е това множество, обединение и сечение на множества и как се решават задачите, свързани с тях по метод, наречен Кръгове на Ойлер.

Всъщност около нас е пълно с най-различни множества! Множеството на учениците от твоя клас, множеството на планетите в Слънчевата система, множеството на всички животни от семейство “котки”, множеството на естествените числа и още много, много множества! Да видим кое е общото и различното между тях.
Какво представляват множествата
Множествата всъщност, са съвкупност от обекти, които са обединени от някакво общо свойство. Всички обекти, които попадат в множеството, се наричат негови елементи.
Например множеството на учениците от 71.СУ включва всички ученици, които се обучават в това училище. Всеки един от учениците е отделен елемент на множеството.
Има специален начин да се записват множествата и техните елементи— за множествата се използват големи букви — A,B,C,D…, а елементите им се записват във фигурни скоби { }.
Да зададем множеството А на всички прости числа, по-малки от 20:
A = { 2, 3, 5, 7, 11, 13, 17, 19}
Има и специален начин да запишем, че някой елемент принадлежи към дадено множество:
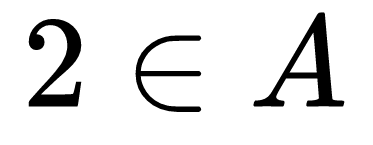
Чете се 2 принадлежи на множеството А.
Можем да запишем, че числото 1 не принадлежи на нашето множество като задраскаме знака за принадлежност.
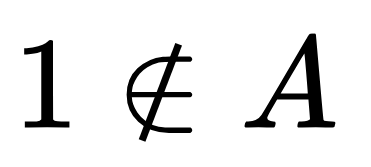
Нека опишем множество B, което съдържа част от елементите на множеството А:
B = { 2, 3, 5, 7, }
Казваме, че B е подмножество на А и записваме:

Важно е да отбележим, че всички елементи на множеството B се съдържат в множеството А!

Всички тези символи и специален начин за описание на множества, подмножества и техните елементи, са като напълно различен език! Важно е да умеем да четем и записваме с тях, за да бъдат нашите задачи правилно и добре структурирани.
Обединение и сечение на множества
Хайде да дефинираме две множества и да видим какви операции може да извършваме с тях!
Нека множество А е съставено от всички положителни двуцифрени числа, които са кратни на 10, а множество B е съставено от всички положителни двуцифрени числа, кратни на 5, които са по-големи от 20 и по-малки от 50.
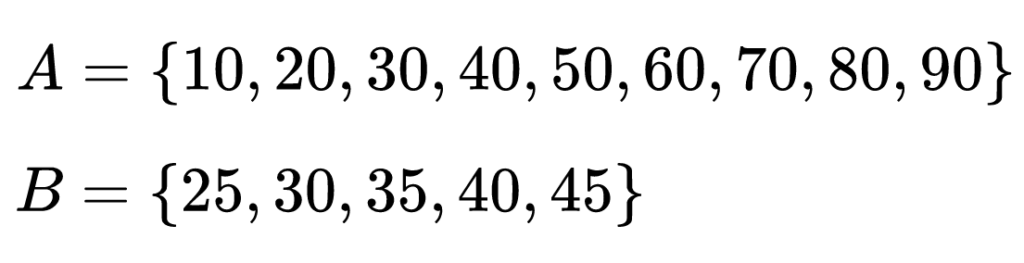

Обединението на двете множества е множество, което е съставено от всички елементи на двете множества. Ако имат общи елементи, те са записват само по веднъж.
Сечението на две множества съдържа всички елементи, които са едновременно елементи и на двете множества.
Обединението на нашите две множества включва всички елементи на първото множество и трябва да добавим числата 25,35,45 от второто множество. Общите елементи ги записваме само веднъж.
Ето как ще зададем обединението на нашите двете множества A и B (числата са подредени по големина):
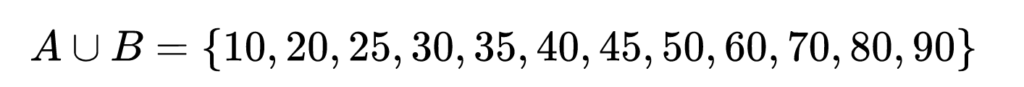
Сечението на нашите две множества има само два елемента, тъй като единствените общи числа са 30 и 40. Записваме обединението ето така:
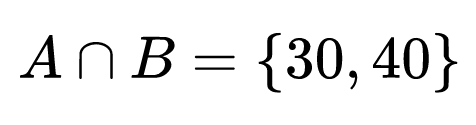
Кръгове на Ойлер

Леонард Ойлер е швейцарски математик, физик и астроном, който е въвел един много лесен и нагледен начин за представяне на множества! При него всяко множество се изобразява с кръг, а вътре в него се записват елементите на множеството.
По този начин много лесно се определят сечението и обединението на множества!
Да покажем с кръгове на Ойлер следните две множества от числа—множеството на едноцифрените нечетни числа, означено с M и множеството на простите едноцифрени числа, означено с N:
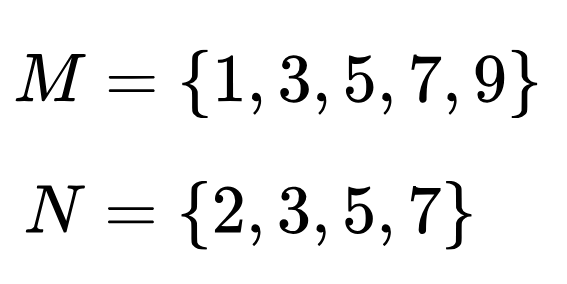
Да представим с кръгове двете множества, като не забравяме, че те имат общи елементи, които ще попаднат в сечението им.
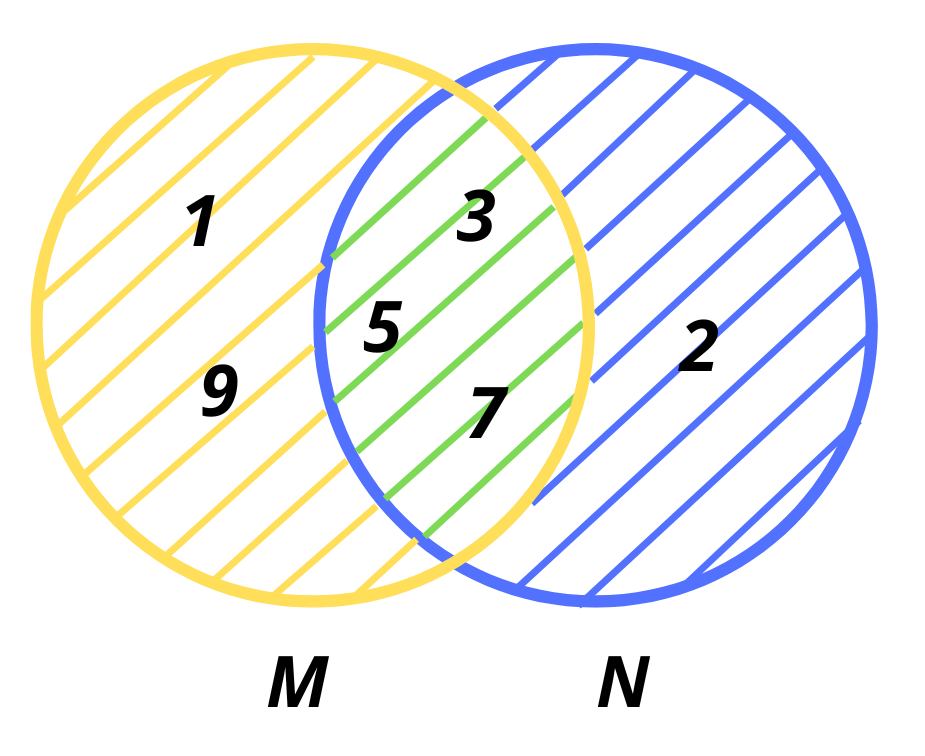
Общите елементи попадат в сечението на множествата, което е защриховано в зелен цвят. В жълтата част на кръга, изобразяващ множествотo M, попадат елементите, които се срещат само в това множество, а със син щрих е числото 2, което е елемент само на множеството N.
Състезателна задача с кръгове на Ойлер
Учениците от 6.А и 6.Б клас участвали в спортния празник на училището. От всички деца 19 участвали във футболния турнир, 17 се състезавали във волейболното състезание, а 7 от тях взели участие и в двете съревнования. Колко са всички деца от двата класа?
Първо начертаваме двата кръга, които изобразяват множествата на играещите футбол и волейбол. Имаме 7 ученика, които участват и в двете състезания, те попадат и в двете множества, затова ги записваме в сечението на множествата (в общата част на двата кръга).
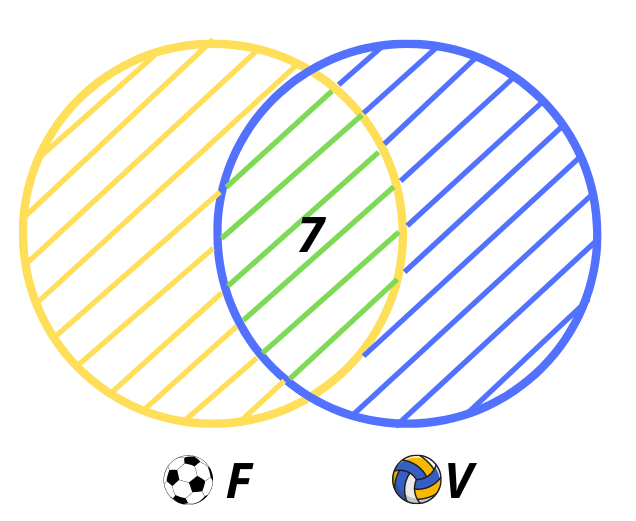
Във футболния турнир са участвали 19 ученика, но от тях 7 са взели участие и в другия турнир. Тогава учениците, които са играли само футбол, са 19 — 7 = 12. Записваме ги в кръга, който показва множеството на играещите футбол, но така че да не попадат в сечението на двете множества. Ето така:
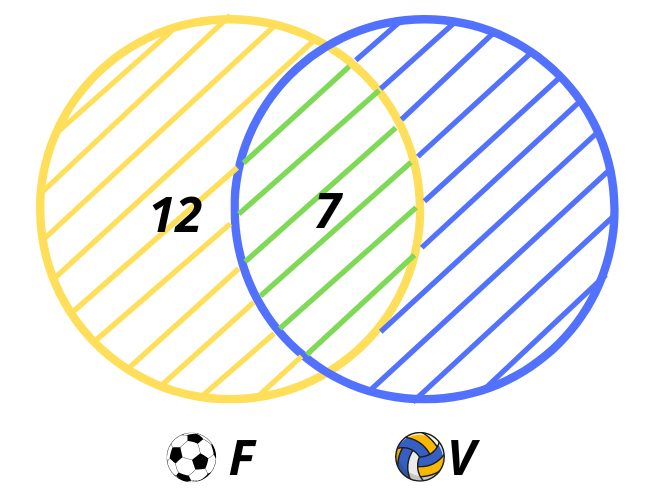
Децата, които са играли волейбол са 17, но от тях 7 са играли и футбол. Тогава само волейбол са играли 17 — 7 = 10 деца. Записваме ги в кръга на множеството на играещите волейбол, ето така:
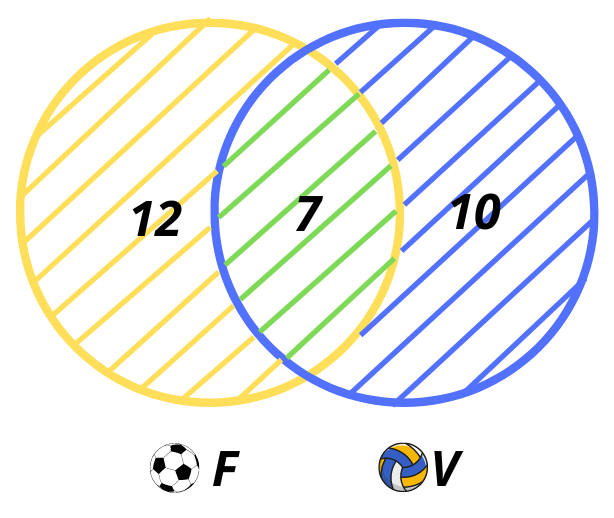
Вече сме готови и можем да пресметнем колко са всички ученици в шестите класове! Трябва само да съберем броя на децата, които са играли само футбол, които са играли футбол и волейбол и тези, които са играли само волейбол:
12 + 7 + 10 = 29 ученика

Харесаха ли ви задачите с множества? Много полезни и интересни са, така че се упражнете със следващия тест!
Не забравяй да разгледаш и мисловната карта към урока!