Привеждане на обикновени дроби към най-малък общ знаменател
Здравей, приятелю на математиката!
Днешният урок е много важен, тъй като в него ще научим за една от най-важните операции при събиране и изваждане на обикновени дроби, а именно ще разберем какво е привеждане на обикновени дроби към най-малък общ знаменател. Както и как да записваме различни дроби като такива с равни знаменатели.
Последвай ме и днес, за нови математични приключения!
1. Какво е най-малък общ знаменател?
Когато работим с дроби, понякога трябва да ги сравняваме или събираме. За да направим това, дробите трябва да имат същия знаменател.Замяната на две или повече дроби, които имат различни знаменатели, с еднакви наричаме привеждане на обикновените дроби към общ знаменател.

Две или повече обикновени дроби са приведени към общ знаменател, когато намерим НОК на техните знаменатели.
2. Как да намерим най-малкия общ знаменател (НОЗ)?
- Намираме знаменателите на дробите: Например, ако имаме дробите 2/5 и 3/4, то техните знаменатели са 5 и 4.
- Определяме кратните на всеки знаменател: Например, кратните на 5 са: 5, 10, 15, 20, 25 и т.н., а кратните на 4 са: 4, 8, 12, 16, 20, 24 и т.н.
- Намираме най-малкото общо кратно НОК: В нашият пример, НОК на 5 и 4 е 20. Това означава, че 20 е най-малкият общ знаменател за дробите 2/5 и 3/4.
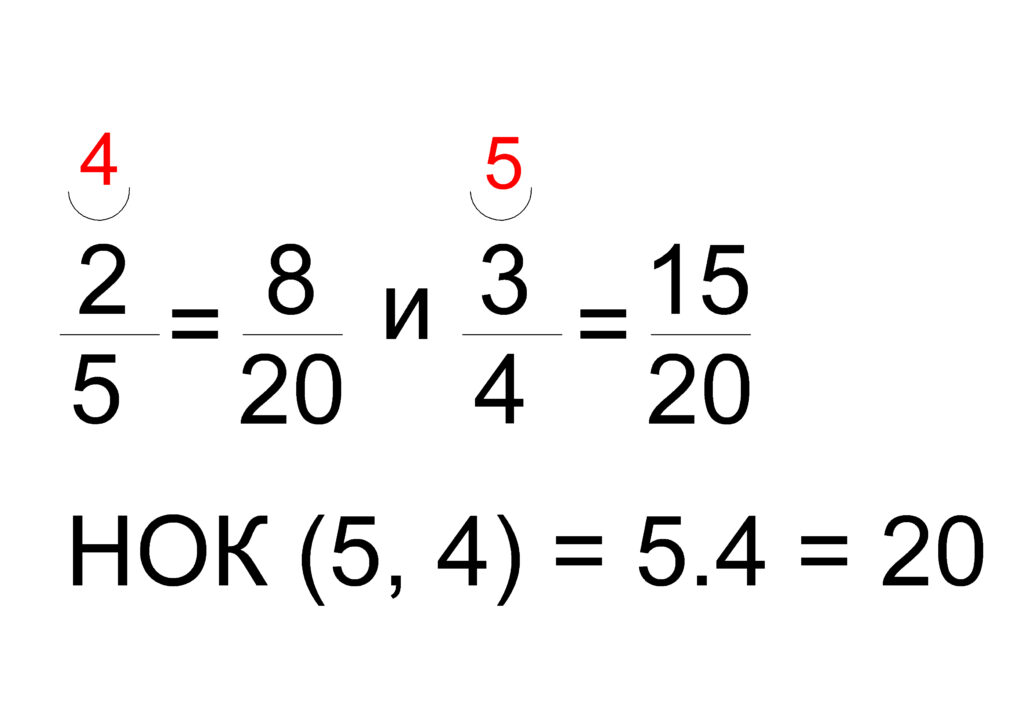
3. Как да приведем дробите към НОЗ?
- Определяме най-малкия общ знаменател (както е описано по-горе).
- Преобразуваме дробите. За целта умножаваме числителя и знаменателя на всяка дроб, така че новият знаменател да е равен на НОЗ. Например:
- За обикновената дроб 2/5: За да приведеш 2/5 към знаменател 20, трябва да умножим числителя и знаменателя на дробта с 4 (тъй като 5 × 4 = 20). Получаваш 2 × 4 / 5 × 4 = 8/20.
- За обикновената дроб 3/4: За да приведеш 3/4 към знаменател 20, трябва да умножим числителя и знаменателя на дробта с 5 (тъй като 4 × 5 = 20). Получаваш 3 × 5 / 4 × 5 = 15/20.

Допълнителните множители при всяка обикновена дроб се получават, като се раздели намерения от нас общ знаменател на предходния знаменател на всяка от тези дроби.
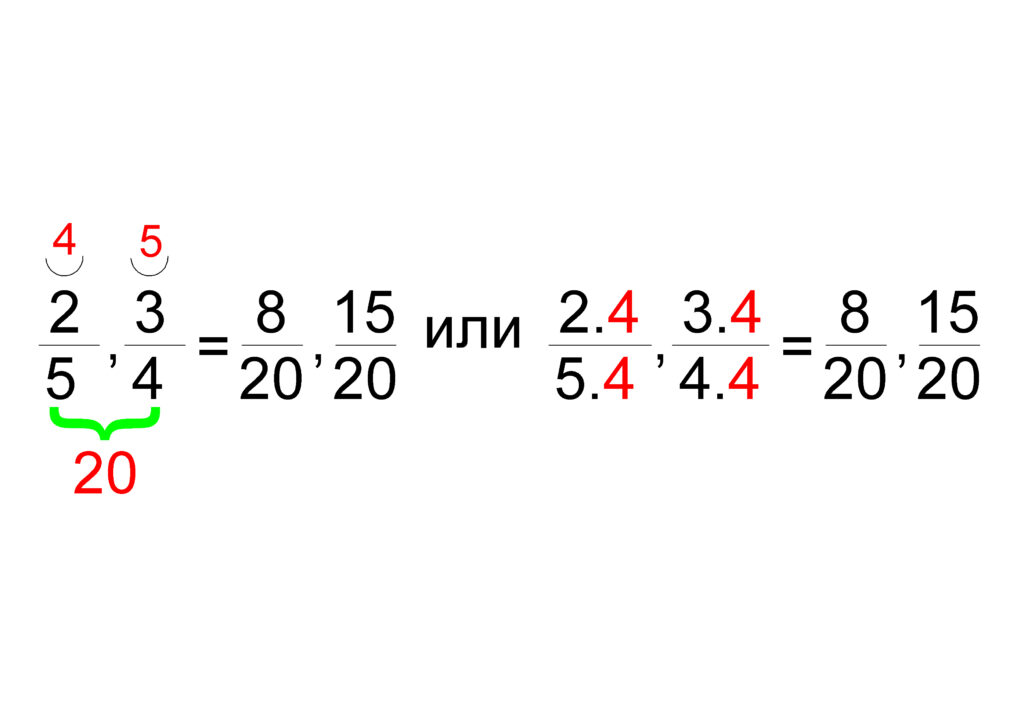

Когато се привежда към общ знаменател цяло число, то се записва като дроб със знаменател 1.
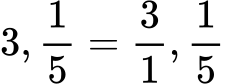
4.Изчислителни задачи
- Приведете дробите към най-малък общ знаменател:
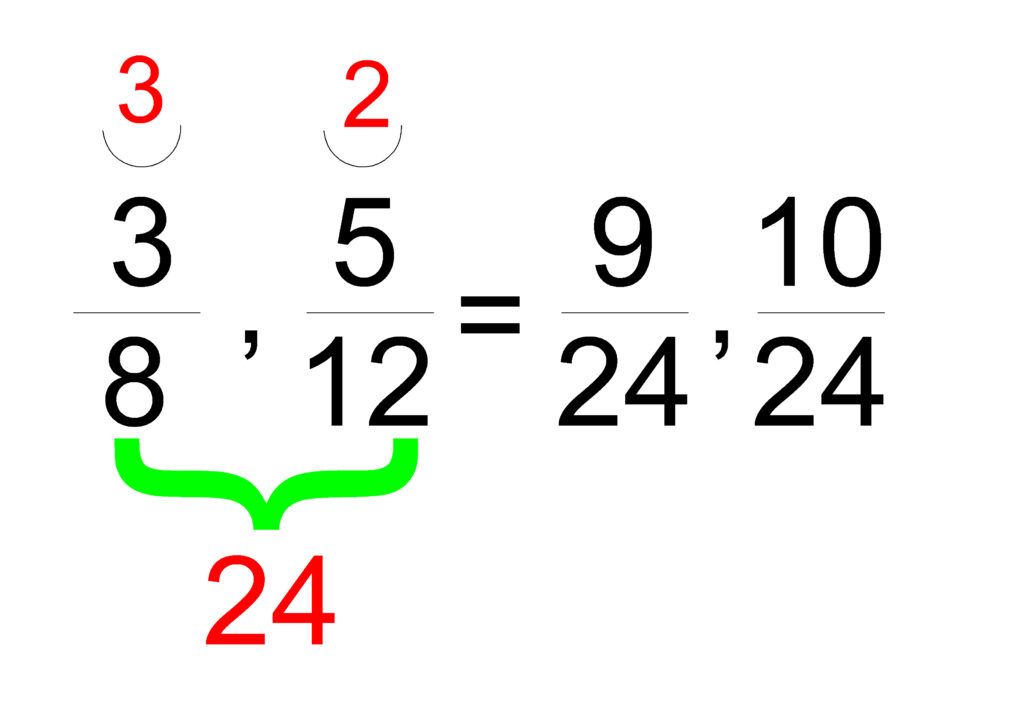
3/8 и 5/12
Решение:
- Намираме НОЗ на 8 и 12. Това е 24.
- Привеждаме 3/8 към знаменател 24: 3 × 3 / 8 × 3 = 9/24.
- Привеждаме 5/12 към знаменател 24: 5 × 2 / 12 × 2 = 10/24.
2. Приведете дробите към най-малък общ знаменател:
7/10 и 2/15
Решение:
- Намираме НОЗ на 10 и 15. Това е 30.
- Привеждаме 7/10 към знаменател 30: 7 × 3 / 10 × 3 = 21/30.
- Привеждаме 2/15 към знаменател 30: 2 × 2 / 15 × 2 = 4/30.
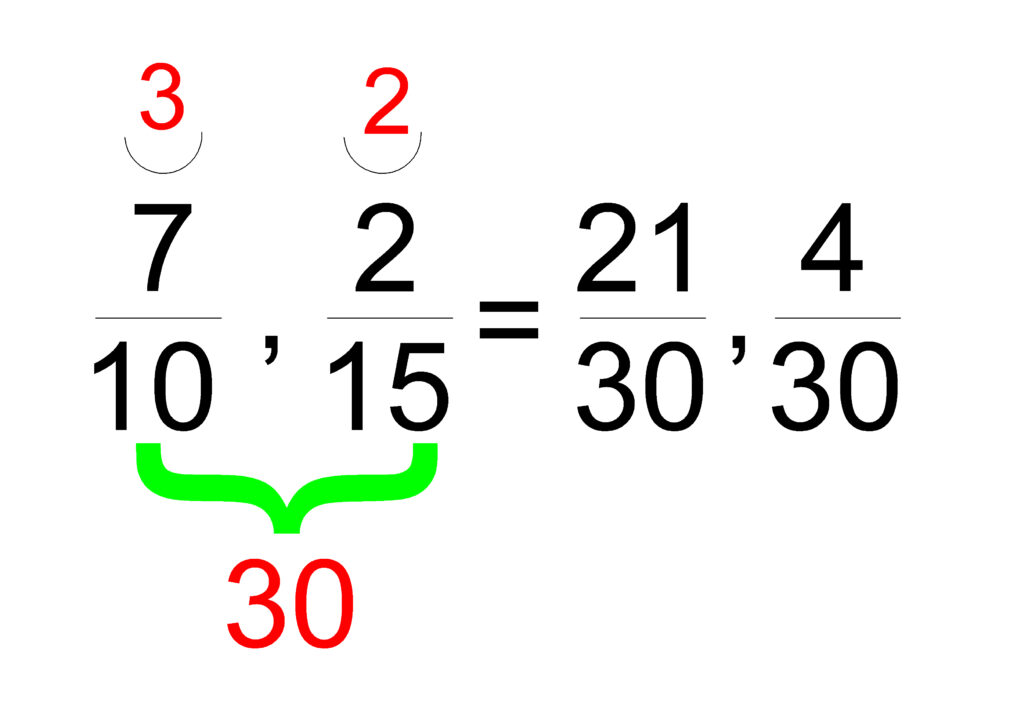
5. Текстови задачи
- На сергия били подредени различни плодове, като 1/6 от тях били круши, 7/18 ябълки, а останалите 4/9 дини. Колко са плодовете на сергията, ако те не са повече от 20? Какъв е броят на крушите, ябълките и ягодите?

Решение:
- Намираме НОК на 6; 18 и 9.
- Привеждаме трите обикновени дроби към НОЗ.
- Умножаваме допълнителните множители по числителите.
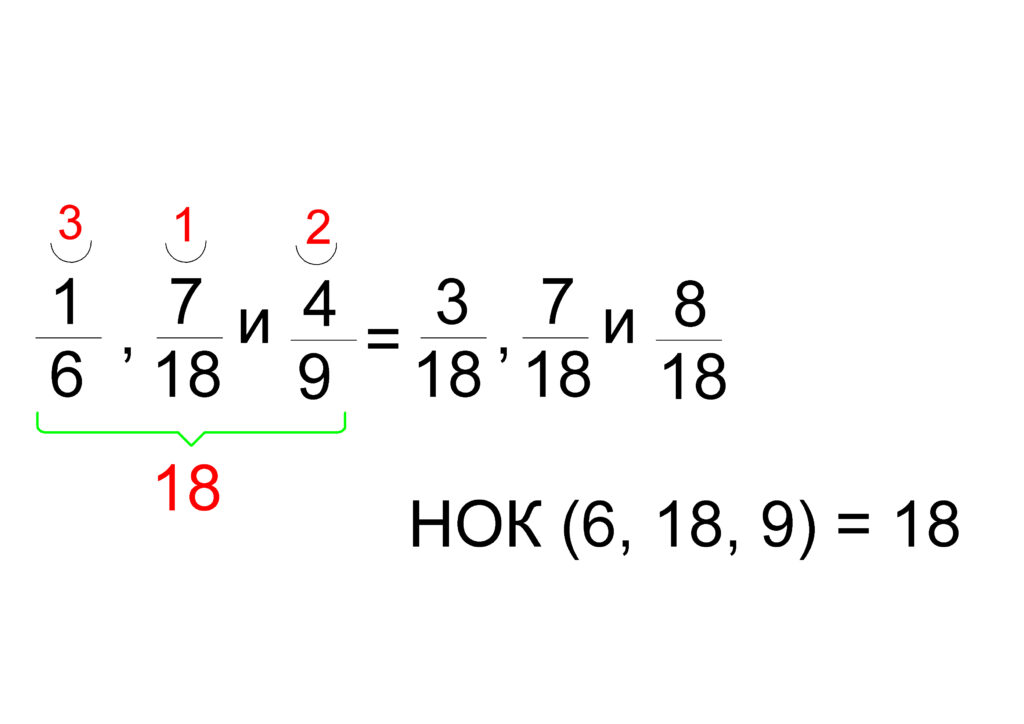
Следователно виждаме, че знаменателя е 18. Следователно плодовете на сергията са 18. От получените, след привеждане под НОЗ, числители виждаме, че броят на крушите е 3; на ябълките – 7 и на дините – 8.
6. Практически задачи
- В сладкарница доставили 15 парчета торта. 2/5 от тези парчета били торта “Гараш”; 1/3 френска торта и 4/15 ванилова торта. Колко на брой са парчетата торта “Гараш”; френска и ванилова торта?

Решение:
- Намираме НОК на 5, 3 и 15. Той е 15.
- Привеждаме дробите към НОЗ.
- Умножаваме допълнителните множители по числителите.
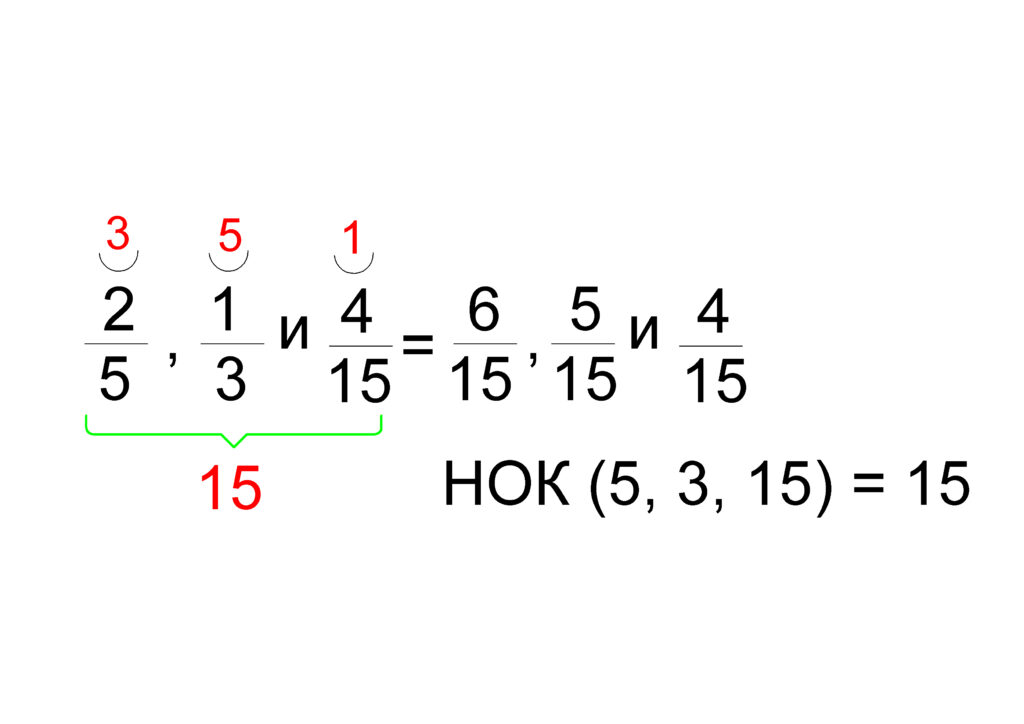
След като приведем об. дроби към НОЗ виждаме, че броят на парчетата торта “Гараш” са 6; парчетата френска торта са 5 и ваниловата торта е 4.