Стандартен запис на число
Здравейте, приятели! Урокът ни днес е много важен и страшно интересен! Ще разберем какво е това стандартен запис на число и къде се използва.

Понякога ни се налага да работим с много големи числа (в астрономията и физиката).Ако трябва да запишем, например, колко е разстоянието между две планети. Друг път пък ни трябват изключително малки числа (в химията и биологията)! Например, когато измерваме разстоянието между ядрата на два атома. В такива случаи е удобно да записваме числата в така наречения стандартен запис, който ни помага да не пишем твърде големи или твърде малки числа.
Записване на числата със степени на числото 10
Всяко едно число в десетичната бройна система може да се запише като се използват степени на числото 10. Хайде да видим първо с едно цяло число как ще се получи— 42 367. Това число има:
- 7 единици
- 6 десетици
- 3 стотици
- 2 хиляди
- 4 десетохиляди
А сега да помислим как можем да ги представим като степен на числото 10:
- 7.1 = 7. 100
- 6.10 = 6. 101
- 3.100 = 3. 102
- 2.1000 = 2. 103
- 4.10000 = 4. 104
Готови сме вече да запишем нашето число като сбор, в който използваме степените на числото 10.
42 367 = 4. 104 + 2. 103 + 3. 102 + 6. 101 + 7.100
А сега да видим как ще запишем дробната част на десетичните дроби. Например числото 0,745
- 7 десети
- 4 стотни
- 5 хилядни
Да помислим сега как ще изглеждат записани като използваме степени на числото 10
- 7 . 1/10 = 7. 10—1
- 4. 1/100 = 4 . 10—2
- 5. 1/1000 = 5 .10—3
А сега да представим числото като сбор:
0,745 = 7. 10—1 + 4 . 10—2 + 5 .10—3
Стандартен запис на число
За да е записано едно число със стандартен запис, то трябва да запишем произведение, което изглежда ето така:
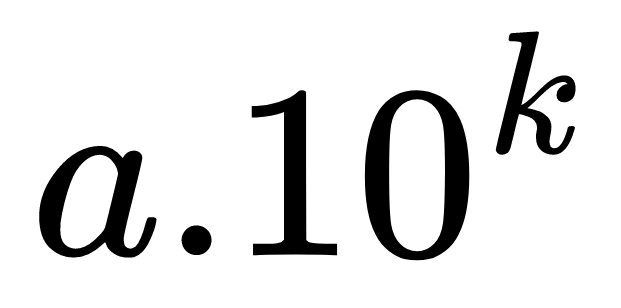
Числото a трябва да е по-голямо или равно на 1 и по-малко от 10, а к трябва да е цяло число.
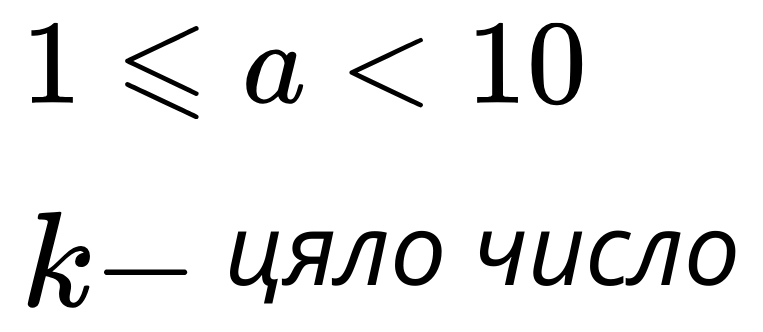
к се нарича порядък на числото. Числото 3.104 е от порядък 4, а числото 6.10—5
е от порядък —5.

Стандартният запис на число има голяма приложение в практически задачи, свързани с природните науки. Много е важно обаче да не забравяме, че има условия как да се записва той!
Записване на много големи числа със стандартен запис на число
Хайде да запишем разстоянието от Земята до Луната със стандартен запис. Средното разстояние е 384 403 km, закръгляваме го с точност до хилядите на 384 000 km
За да го запишем със стандартен запис, трябва да отделим първо число, което да е по-малко от 10 и по-голямо или равно на 1. Ами това ще е числото 3,84. Сега да помислим по колко ще го умножим, за да получим 384 000 km. Ами точно по 100 000, което пък е равно на 105. Тогава сме готови да запишем стандартния запис на числото:
384 000 km = 3,84 . 105 km

Много често разстоянието между небесните тела се измерва във светлинни години. Една светлинна година e разстоянието, което светлината изминава за една година във вакуум. Приблизително тя е равна на малко над 9,46.1012 km.
Да видим как ще запишем със стандартен запис разстоянието, което е изминал марсохода “Спирит”, за да пропътува разстоянието от Земята до Червената планета.
Това разстояние непрекъснато се променя, средната му стойност е 225 000 000 km.
За да го запишем със стандартен запис, трябва да помислим кое число, ще е по-малко от 10 и по-голямо или равно на 1. Ами това число е 2,25. За да получим 225 000 000, трябва да го умножим с 108.
225 000 000 km = 2,25 . 108 km
Записване на много малки числа със стандартен запис на число

Когато изследваме молекулите на веществата, работим с много малки числа. Удобна мерна единица за дължина е нанометърът (nm), който е равен на една милиардна част от метъра.
Записва се 1 nm = 1.10—9 m
Молекулата на кислорода е с размер е 0,346 nm. Трябва да запишем числото със стандартен запис в метри.
Вече научихме, че 1 nm = 1.10—9 m, тогава 0,346 nm ще са равни на 0,346. 10—9 m.
Това обаче, не е стандартен запис на число, тъй като първия множител е по-малък от 1.
Можем да запишем 0,346 като 3,46.0,1= 3,46 . 10-1
За размерът на молекулата на кислорода се получава :
0,346 nm = 3,46 . 10-1 nm = 3,46 . 10-1. 10-9 m = 3,46 . 10-10 m

Прокариотите са микроскопични организми и учените смятат, че те са дали началото на всички форми на живот, които познаваме. Размерите на прокариотните клетки започват от 0,2 микрмометра.
Нека запишеш размерът на най-малките прокариатните клетки в метри като използваме стандартен запис на число.
Първо трябва да знаем, че 1 микрометър е равен на една милионна част от метъра.
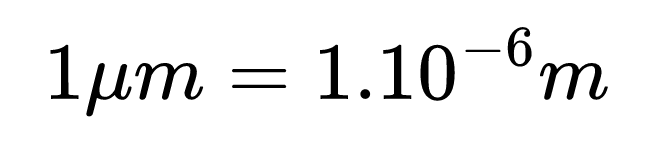
Тогава нашата клетка ще има размер:
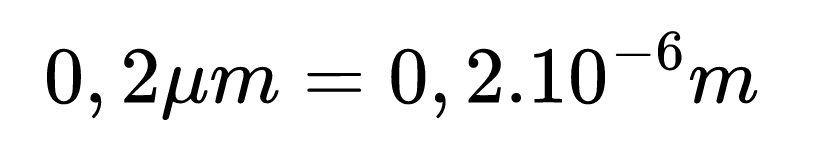
Но 0,2 = 2.0,1 = 2.10—1 . Остава да запишем нашето число в стандартен запис:
0,2.10—6 m = 2.10—1.10—6 m = 2.10—7m
А сега е време да се упражниш с теста!