Степенуване с естествен степенен показател

Здравейте, шестокласници! Днес ще се запознаем с едно съвсем ново действие! Нарича се степенуване и ще ти е много полезно за напред!

Действието степенуване е много важно! Има своето специално място и при определяне на реда на действие при пресмятането на изразите.

Какво е това степенуване?

Степенуването е бърз начин да запишем произведение на равни множители. Например, вместо да пишем 3.3.3.3, записваме степента 3⁴ и четем ” три на четвърта степен”.

Всяка степен има ето тези компоненти (съставни части):

• Основа — показва ни кои са равните множители.
• Степенен показател- показва ни броя на равните множители

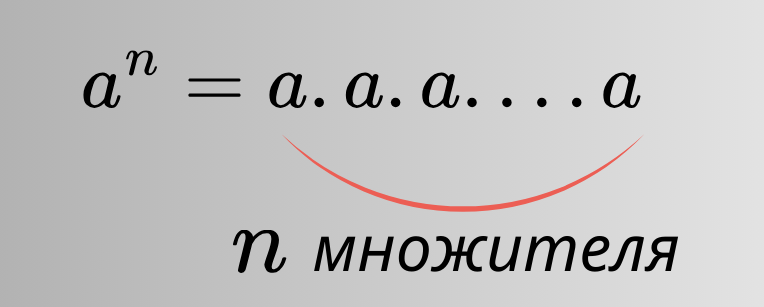
Основата е означена с “а“, а степенният показател с “n”.

Да разгледаме няколко примера как можем да запишем произведение на равни множители като степен:

1,2 . 1,2 . 1,2 . 1,2 . 1,2 = 1,2⁵ ( чете се “едно цяло и две десети на пета степен” )

(—7) . (—7) . (—7) . (—7) = (—7)⁴ ( чете се “минус седем на четвърта степен” )

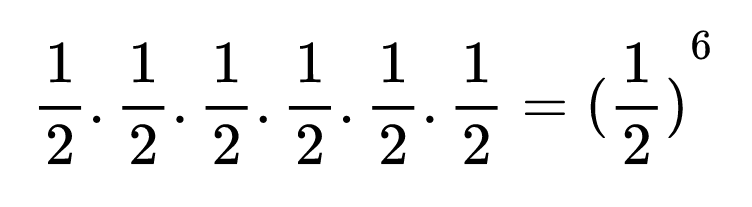
(чете се ” една втора на шеста степен”)

Когато записваме степен с отрицателна основа, основата винаги се записва в скоби!

(—2) . (—2) . (—2) . (—2) = (—2)⁴ = +16

Ако забравим да запишем основата в скоби, ще получим —2⁴, но минусът ни показва, че тук имаме противоположното число на 2⁴, което е —16.

А забеляза ли как записахме степента, когато основата е обикновена дроб ?

Когато основата е обикновена дроб, винаги я записваме в скоби!

Да видим защо е много важно това правило:

Ако не поставим в скоби обикновената дроб, тогава степенуваме само нейния числител. Например:

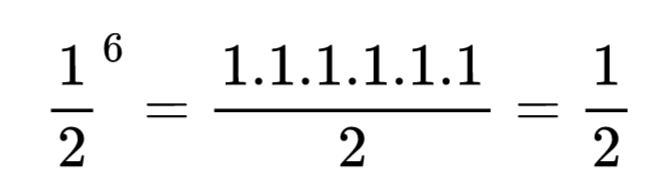
Да видим какво ще получим, ако запишем правилно основата в скоби:

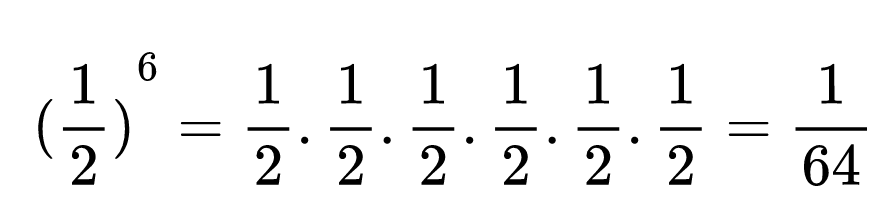
Пресмятане на степени

Много често в задачите трябва да пресметнем степента. Ами това означава да изчислим на колко е равно произведението от равните множители, на което е равна тя.

В началото може да си разписваш подробно произведението, но в един момент ще свикнеш и няма да е нужно. Хайде да запишем подробно следващите три пресмятания на степени.

3⁴ = 3 . 3 . 3 .3 = 9.9 = 81

(—7)³ = (—7).(—7).(—7) = 49 .(—7) = — 343

(—2)⁴ = (—2) . (—2) . (—2) . (—2) = 4.4 = 16

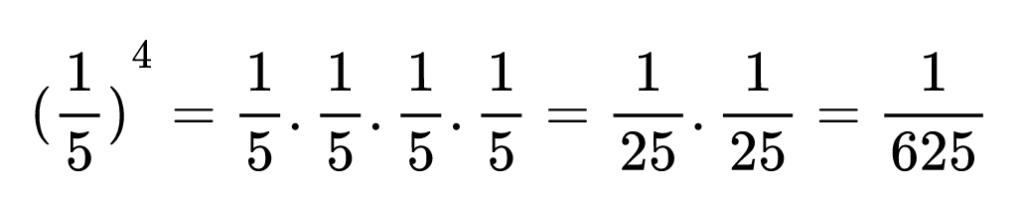
Забеляза ли, че когато имаме степен с отрицателна основа, но степенният показател е четно число, степента има положителна стойност?

(—2)⁴ = 16

Това се получава, защото произведението, на което е равна степента, има четен брой отрицателни множители.

Стойността на степен с отрицателна основа и степенен показател, който е нечетно число, е винаги отрицателно число!

(—7)³ = —343

В този случай произведението, на което е равна степента, е с нечетен брой отрицателни множители.

Можеш да си припомниш тези правила в ето тази статия: Умножение и деление на рационални числа

Ред на действие в изрази със степенуване, в които няма скоби

Когато в израза няма скоби, първо се извършва степенуването, а след това се спазва редът, който вече познаваме:

• Степенуване
• Умножение и деление
• Събиране и изваждане

Хайде да решим един пример, за да разберем реда на действие:

—7,5 + (—2)³ + 7,5. (—1/2)²

Първо ще извършим степенуването:

—7,5 + (—8)+7,5.1/4

Нека да пресметнем произведението и след това ще имаме само събираеми, които да комбинираме, както преценим.

—7,5 + (—8) + 7,5.0,25 = —7,5 —8 +1,875

Хайде да съберем първо двете отрицателни числа и след това да съберем получения сбор с положителното число:

—7,5 —8 +1,875 = —15,5 + 1,875 =

= —13,625

Можем да спестим малко писане, ако едновременно с умножението извършим събирането на две отрицателни числа. Ето така:

—7,5 + (—8) + 7,5.0,25 = —15,5 + 1,875 =

= —13,625

Ред на действие в изрази със степенуване, когато има скоби

Когато в израза има скоби, първо се извършва действието в скобите, а след това се спазва редът, който описахме по-горе:

• действие в скобите
• степенуване
• умножение и деление
• събиране и изваждане

Хайде, да упражним правилото с един пример!

(—2,5:0,2+3,5)² — (7.0,05+4) — (—3—1)²

Нека първо извършим изчисленията в скобите:

(—25:2+3,5)² — (0,35+4)—(—4)² =

= (—12,5+3,5)² — 4,35 — (+16) =

= (—9)² — 4,35 — 16

Тук можем да пресметнем степента и да запишем сбора на двете отрицателни числа:

= 81 — 20,35 = 60,65

Можеш да упражниш урока със следващия тест! Не забравяй, че математиката се учи с решаване на много задачи!