Най-голям общ делител (НОД)

Здравейте, ученици! Днес ще научим за един много важен математически термин – най-голям общ делител (НОД). Ще разберем какво представлява, как да го намираме и защо е полезен. Ще разгледаме няколко примера и ще решим задачи, за да затвърдим знанията си. Готови ли сте? Да започваме!

1. Какво е най-голям общ делител (НОД)?

Най-големият общ делител на две или повече числа е най-голямото число, което дели тези числа без остатък. Нека разгледаме един пример, за да разберем по-добре.

Пример 1: Намерете на НОД на 12 и 18

1. Намираме делителите на 12:
   • Делители на 12 са: 1, 2, 3, 4, 6, 12.
2. Намираме делителите на 18:
   • Делители на 18 са: 1, 2, 3, 6, 9, 18.
3. Намираме общите делители:
   • Общите делители на 12 и 18 са: 1, 2, 3, 6.

Числото, което е делител на няколко числа се нарича общ делител на тези числа.

4. Най-големият от тези общи делители е 6.
   • Значи НОД(12, 18) = 6.

Най-голям общ делител на няколко числа е най-големият от техните общи делители. Някои числа нямат друг общ делител освен числото 1. Такива числа наричаме взаимно прости. Например, 8 и 9 са взаимно прости числа. Техният общ делител е само числото 1.

2. Как да намерим НОД?

Има няколко метода за намиране на НОД, но ние ще се съсредоточим върху два от тях:

1. Чрез изброяване на делителите (както направихме в примера по-горе).
2. Чрез разлагане на прости множители.

Пример 2: Намиране на НОД чрез разлагане на прости множители

Нека намерим НОД на 36 и 48.

1. Разлагаме 36 на прости множители:
   • 36 = 2 × 2 × 3 × 3, можем да запишем и така: 2² × 3² (чете се 2 на 2-ра степен и 3 на втора степен).
2. Разлагаме 48 на прости множители:
   • 48 = 2 × 2 × 2 × 2 × 3, можем да запишем и така: 2⁴ × 3 (чете се 2 на 4-та степен и 3 на първа степен).
3. Намираме общите прости множители с най-малките степени:
   • Общи прости множители са 2 и 3.
   • Най-малките степени са 2² и 3¹.
4. НОД е произведението на тези множители:
   • НОД(36, 48) = 2² × 3¹ = 4 × 3 = 12.

3. Изчислителни задачи

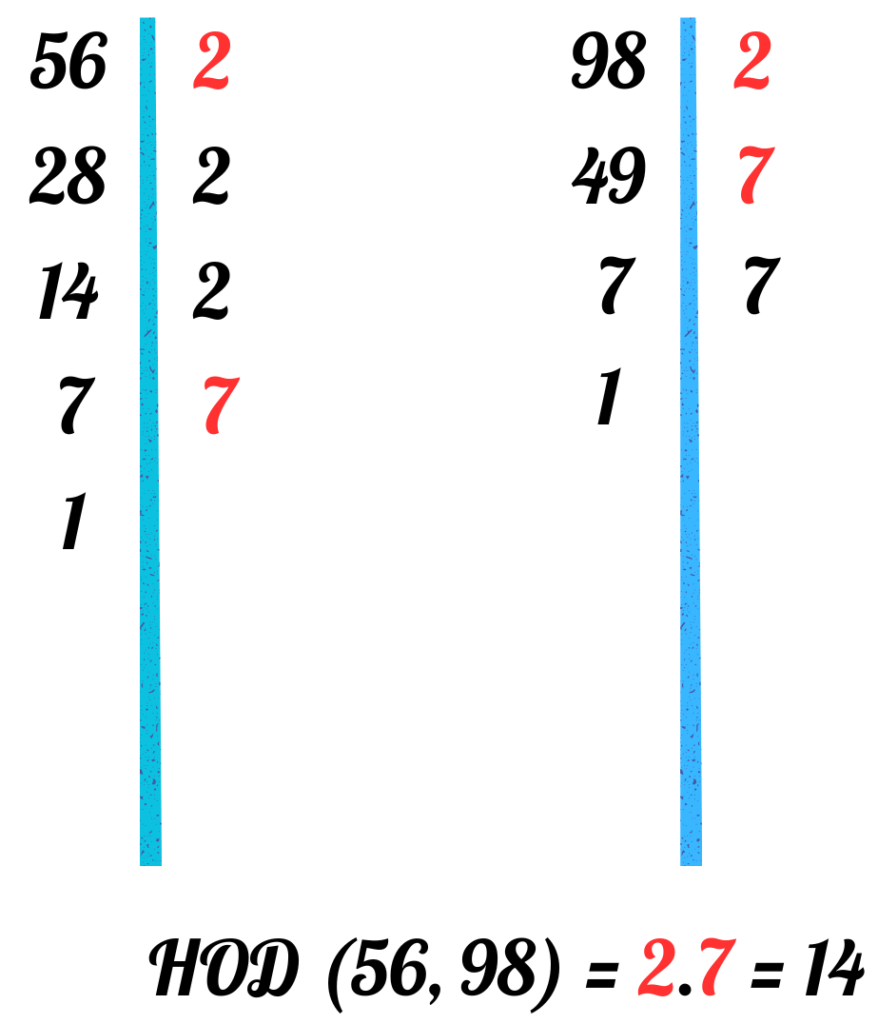
Задача 1: Намерете НОД на 56 и 98.

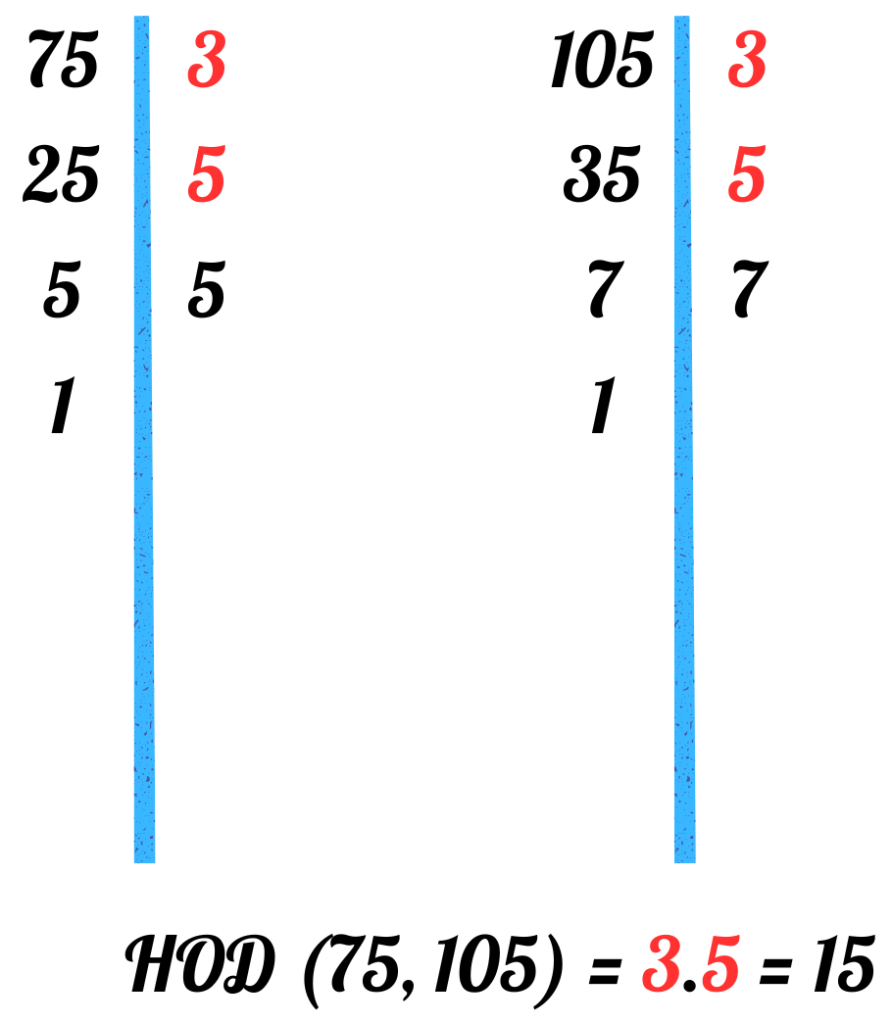
Задача 2: Намерете НОД на 75 и 105.

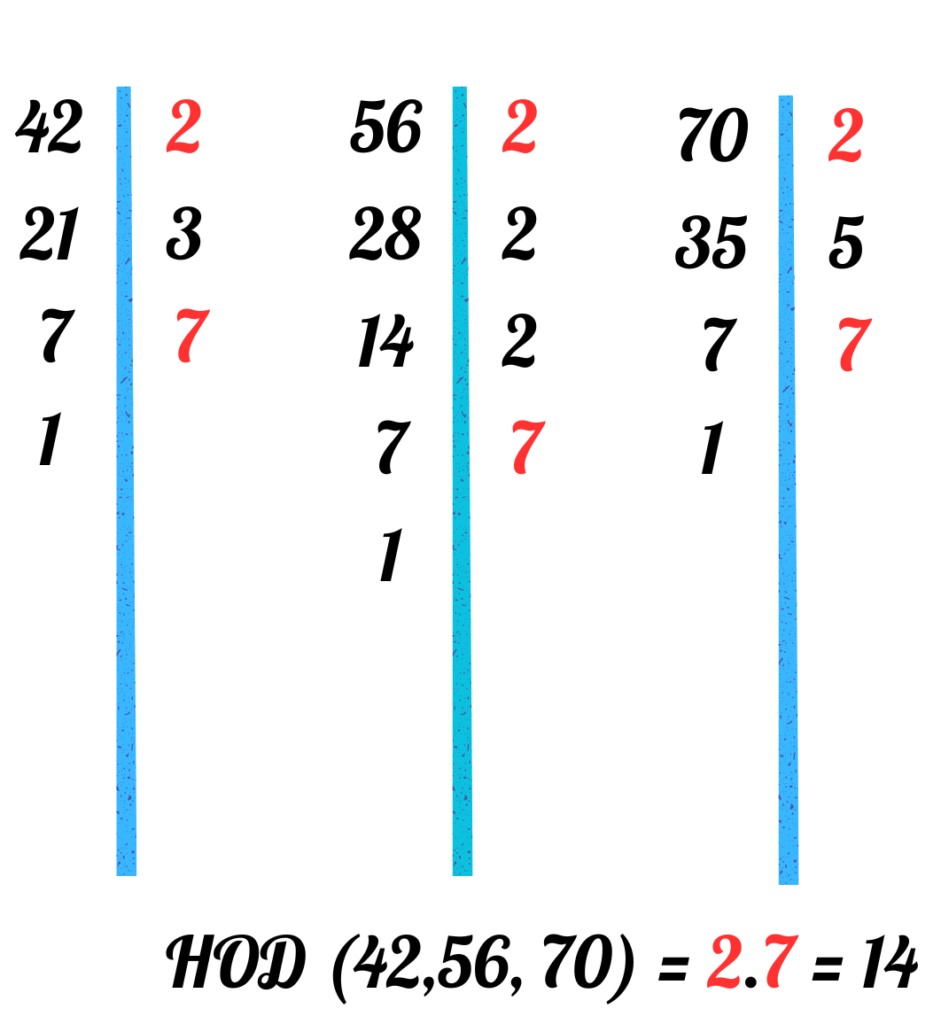
Задача 3: Намерете НОД на 42, 56 и 70.

4. Отговори на изчислителните задачи:

Задача 1:

• Делители на 56: 1, 2, 4, 7, 8, 14, 28, 56.
• Делители на 98: 1, 2, 7, 14, 49, 98.
• Общи делители: 1, 2, 7, 14.
• Най-големият общ делител е 14.
• Отговор: НОД (56, 98) = 14.
• Можем да решим задачата и така:

Задача 2:

• Делители на 75: 1, 3, 5, 15, 25, 75.
• Делители на 105: 1, 3, 5, 7, 15, 21, 35, 105.
• Общи делители: 1, 3, 5, 15.
• Най-големият общ делител е 15.
• Отговор: НОД (75, 105) = 15.
• Можем да решим задачата и така:

Задача 3:

• Делители на 42: 1, 2, 3, 6, 7, 14, 21, 42.
• Делители на 56: 1, 2, 4, 7, 8, 14, 28, 56.
• Делители на 70: 1, 2, 5, 7, 10, 14, 35, 70.
• Общи делители: 1, 2, 7, 14.
• Най-големият общ делител е 14.
• Отговор: НОД (42, 56, 70) = 14.
• Можем да решим задачата и така:

5. Текстови задачи

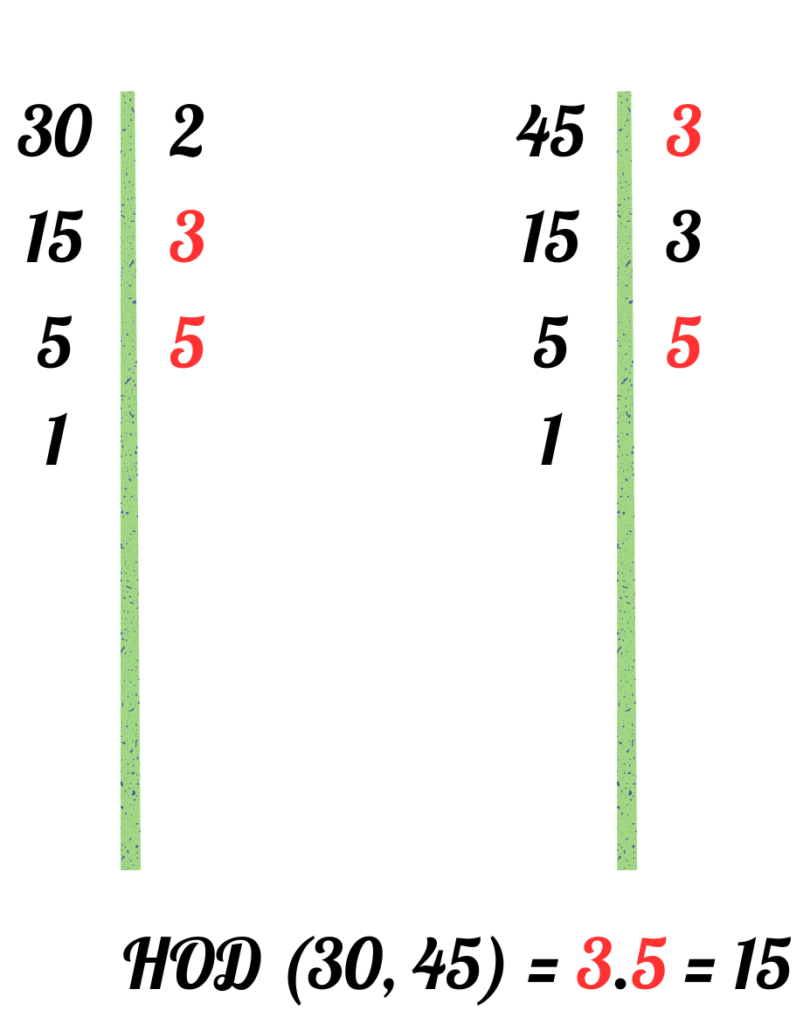
Задача 4: В една градина има 30 ябълки и 45 круши. Градинарят иска да разпредели плодовете в кошници, така че във всяка кошница да има еднакъв брой ябълки и еднакъв брой круши. Какъв е максималният брой ябълки и круши във всяка кошница?

• Решение:
  • Намираме НОД(30, 45).
  • Делители на 30: 1, 2, 3, 5, 6, 10, 15, 30.
  • Делители на 45: 1, 3, 5, 9, 15, 45.
  • Общи делители: 1, 3, 5, 15.
  • Най-големият общ делител е 15.
  • Отговор: Максималният брой ябълки и круши във всяка кошница е 15.
  • Можем да решим задачата и така:

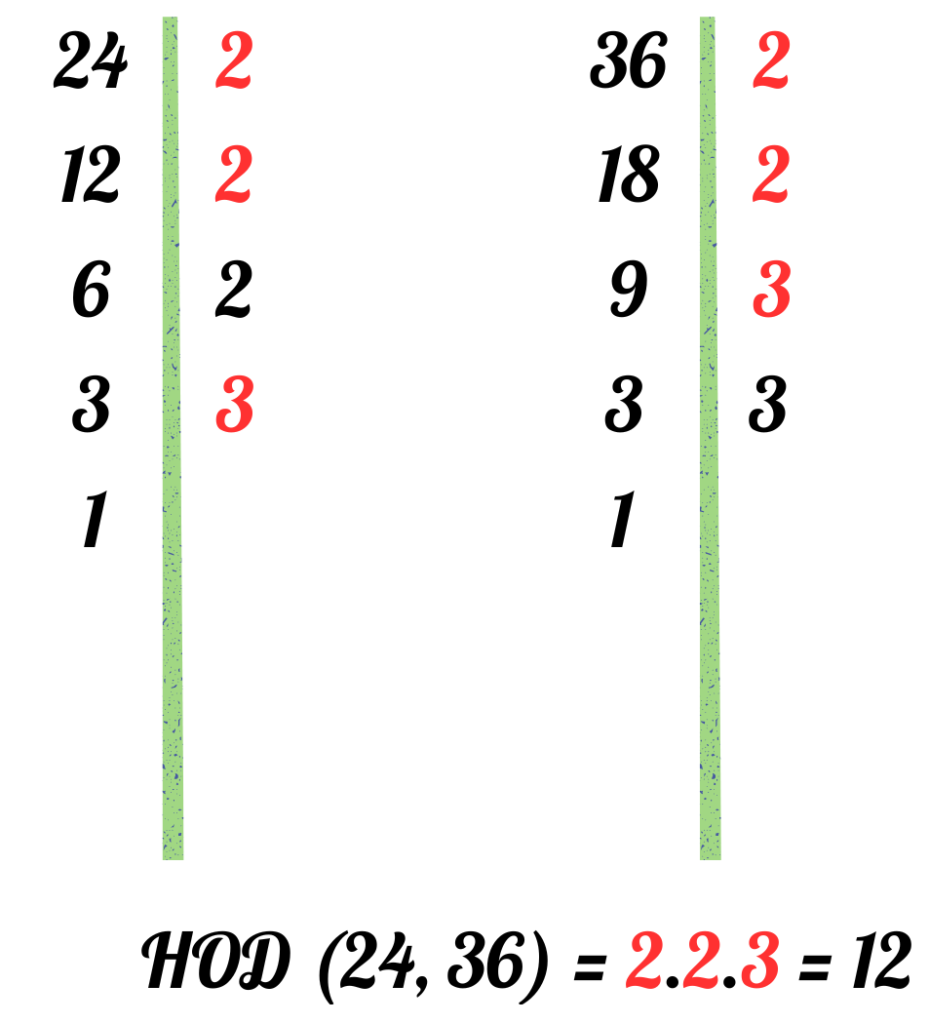
Задача 5: Един учител има 24 маркера и 36 тетрадки. Той иска да раздаде маркерите и тетрадките на учениците си по равно, без да остава нищо. Колко ученика най-много може да има в класа му?

• Решение:
  • Намираме НОД(24, 36).
  • Делители на 24: 1, 2, 3, 4, 6, 8, 12, 24.
  • Делители на 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
  • Общи делители: 1, 2, 3, 4, 6, 12.
  • Най-големият общ делител е 12.
  • Отговор: Учителят може да има най-много 12 ученика в класа.
  • Можем да решим задачата и така:

Надяваме се, че тази статия ви помогна да разберете какво е най-големият общ делител (НОД) и как да го намирате. Успех в решаването на следващите задачи!