Формули за съкратено умножение. Приложение.
Задавали ли сте си въпроса защо понякога в математиката има толкова много скоби? 🤔
Представете си, че трябва да пресметнете (x+7)2 или (15+1)(15−1). Ако разкриваме скобите стъпка по стъпка, ще загубим време и ще рискуваме да сгрешим.
Точно за такива случаи в математиката съществуват формули за съкратено умножение. Те са като малки „магически трикове“, които ни позволяват да прескачаме дългите сметки и да стигаме по-бързо до верния отговор.
Да видим как работят! 🚀
1. Формули за съкратено умножение. Теоретична част
🔹 Трите основни формули

- Квадрат на сбор
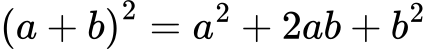
Чете се: „Квадратът на сбор е равен на квадрата на първото събираемо, плюс два пъти произведението на двете събираеми, плюс квадрата на второто събираемо“.
- Квадрат на разлика

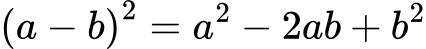
Чете се: „Квадратът на разликата е равен на квадрата на умаляемото, минус два пъти произведението на умаляемото и умалителя, плюс квадрата на умалителя“.
- Разлика на квадрати

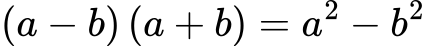
Чете се: „Произведението на сбора и разлика на едни и същи два члена е равно на разликата на квадратите им“.
🔹 Как да ги запомним лесно?
- При квадрат на сбор → средният член е +2ab.
- При квадрат на разлика → средният член е -2ab.
- При разлика на квадрати → няма среден член, защото той се унищожава.
2. Подробни примери и решения
Пример 1 – Квадрат на сбор
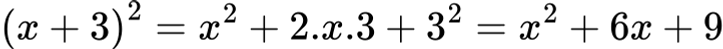
Пример 2 – Квадрат на разлика
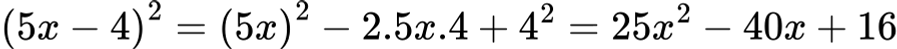
Пример 3 – Разлика на квадрати
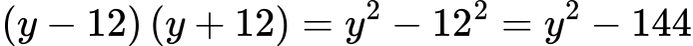
Пример 4 – Бързи изчисления
Намери 49 . 51 = ?
Тук, за по-лесно и бързо решаване, ще използваме формула за съкратено умножение. Можем да решим задачата така:
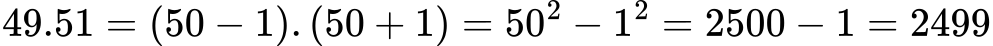
👉 Без формулата трябваше да умножаваме 49 по 51. Сега беше супер бързо и лесно, нали!
Пример 5 – По-сложни изрази
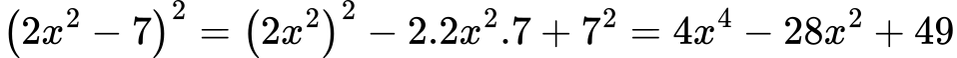
Пример 6 – Приложение в задачи със стойности
Намери 1002 . 998 = ?
Тук, отново за по-лесно и бързо решаване, ще използваме формула за съкратено умножение. Можем да решим задачата така:
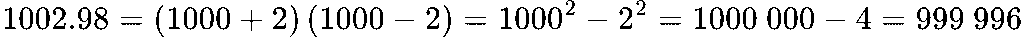
3. Къде се използват тези формули?
- В бързи сметки без калкулатор.
- В преобразуване и съкращаване на алгебрични дроби.
- В уравнения, когато трябва да се опростят големи изрази.
- Във физиката и техниката, където често има квадрати и произведения.
4. Заключение
Формулите за съкратено умножение не са просто правила, които трябва да се научат наизуст. Те са мощен инструмент, който спестява време, усилия и грешки. Колкото повече ги използвате, толкова по-лесно ще решавате задачи.
Запомнете трите „златни формули“:
И винаги ще имате бърз път към верния отговор! 🚀