Здравейте, малки изследователи на геометрията! Днес ще се запознаем с две много специални фигури – успоредник и неговия “по-малък братовчед” – ромб. Те не само че изглеждат интересно, но и имат много интересни свойства, които ги правят важни герои в света на математиката.

Представете си, че сте строители на замъци. Трябва да проектирате здрави основи за стените на вашия замък. Какви форми бихте избрали? Ето тук на помощ идват успоредникът и ромбът – фигури с изключителна стабилност и симетрия. Да се гмурнем в техния свят и да научим повече!

1. Теоретична част: Какво са успоредник и ромб?

1.1. Успоредник – какво представлява?

Успоредникът е четириъгълник, в който срещуположните страни са успоредни и равни по дължина: AB ∥ CD; AD ∥ BC.
👉 Пример: Представете си наклонена кутия за обувки – основата ѝ често е с форма на успоредник.

Срещуположните страни на правоъгълника и квадрата също са успоредни и затова те също са успоредници.

Можем да начертаем успоредник върху квадратна мрежа, като начертаем две успоредни и равни отсечки.

1.2. Свойства на успоредника:

1. Срещуположните страни са равни и успоредни.
2. Срещуположните ъгли са равни.
3. Диагоналите се разполовяват (разделят се на две равни части).

1.3. Ромб – специален вид успоредник

Ромбът е вид успоредник, но с едно специално правило: всички негови страни са равни!

AB = BC = CD = AD = a
👉 Пример: Помислете за формата на диамантa – тя често наподобява ромб.

1.4. Свойства на ромба:

1. Всички страни са равни.
2. Противоположните ъгли са равни.
3. Диагоналите са перпендикулярни (пресичат се под прав ъгъл) и разполовяват ъглите.
4. В ромба всички височини са равни.
5. Има всички свойства на успоредника, защото е негов специален вид.

2. Формули за обиколка и лице

1. Обиколка на успоредник:

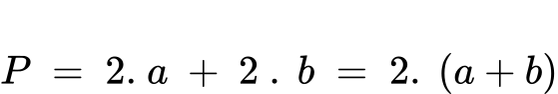
Където:

• a е дължина на основата,
• b е широчина на основата.

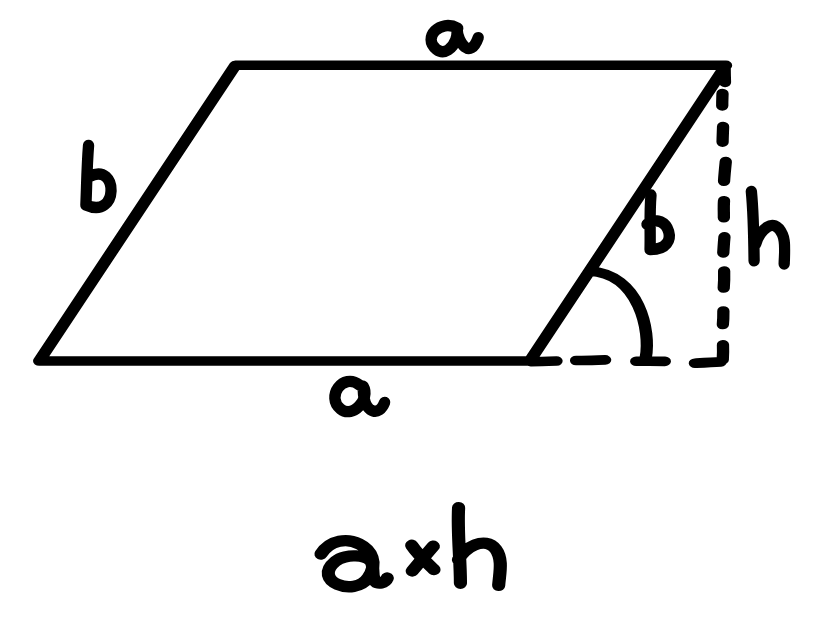
2. Лице на успоредник:

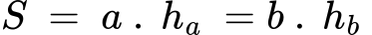
Където:

• a е дължина на основата,
• b е широчина на основата,
• h_a и h_b са височините от връх на успоредника към страните му a и b – разстоянието от основата до срещуположната страна.

3. Обиколка на ромб:

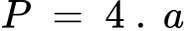
Където:

• a е страна на ромба.

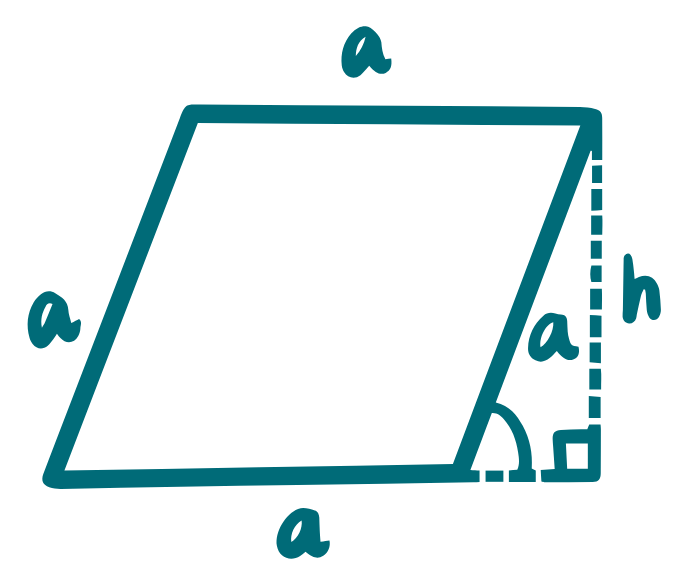
4. Лице на ромб:

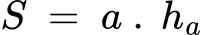
Където:

• a е страна на ромба,
• h_a = h_b e височинa от връх на ромба към страната му a

3. Изчислителни задачи

Задача 1: Намерете лицето на успоредник с основа a = 8 cm и височина h_a = 5 cm.

Решение:

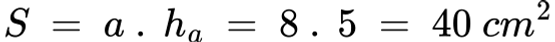
Отговор: Лицето на успоредника е 40 cm².

Задача 2: Ромб има страна a = 10 cm. Намерете неговия периметър.

Решение:

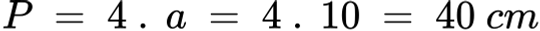
Отговор: Обиколката на ромба е 40 cm.

4. Текстови задачи

Задача 3: Госпожа Петрова решава да шие покривка за маса с форма на успоредник. Основата ѝ е 12 cm, а височината – 6 cm. Колко квадратни сантиметра плат ще ѝ трябват?

Решение:

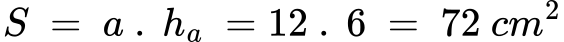
Отговор: Покривката ще има площ 72 cm².

Задача 4: Георги чертае ромб на своя чертеж. Ромбът има страна 5 dm и височина към нея 3 dm. Георги иска да оцвети ромба плътно с червен молив. Какво ще бъде неговото лице?

Решение:

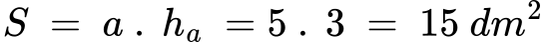
Отговор: Лицето на ромба е 15 dm².

5. Практически задачи

1. Намерете успоредник около вас. Огледайте се вкъщи или в училище. Намерете предмети с форма на успоредник – например книги, дъски или екрани. Измерете тяхната основа и височина, за да изчислите площта им.
2. Нарисувайте ромб. Вземете лист и линия. Нарисувайте ромб с диагонали 10 cm и 8 cm. Измерете диагоналите и проверете дали сте го начертали правилно, като изчислите лицето.
3. Измерете плочки на пода. Ако подът е покрит с плочки с форма на ромб или успоредник, измерете техните страни или диагонали и изчислете лицето на една плочка.

6. Заключение

Успоредникът и ромбът са невероятни фигури с множество приложения – от изкуството до строителството. Те ни учат, че математиката не е просто наука, а език, който описва света около нас. Сега, когато знаете как да работите с тези фигури, използвайте знанията си, за да изследвате и творите. А кой знае – може един ден да проектирате мостове, сгради или дори космически кораби с формата на успоредник и ромб!

Успех, геометрични изследователи! 🚀