Линейни уравнения с дробни коефициенти

Замислял ли си се какво би станало, ако в уравнение вместо цели числа имаме дроби? 🤔
Например 1/2x + 3 = 5
Тези уравнения изглеждат малко по-сложни, но всъщност – с няколко ясни стъпки можеш да ги решаваш лесно и уверено!
В този урок ще научим как да работим с уравнения с дробни коефициенти, ще си припомним понятието корен на уравнение и кога две уравнения са еквивалентни. Ще решаваме примери и ще видим как дробите „изчезват“, когато приложим правилния метод.

1. Теоретична част

1.1. Какво е уравнение?

Уравнение е равенство, в което има неизвестно число, обикновено означено с буква.
Пример:

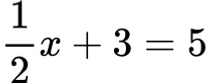
Тук неизвестното е x, а ние трябва да открием стойността на x, която прави равенството вярно.

1.2. Какво е корен на уравнение?

Корен на уравнение наричаме всяко число, което удовлетворява равенството.
Например:

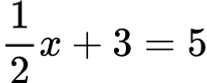
Ако заместим x = 4, получаваме: 1/2⋅4 + 3 = 2 + 3 = 5

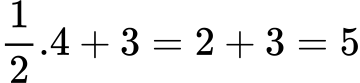
Равенството е вярно → коренът е x = 4.

1.3. Еквивалентни уравнения

Две уравнения са еквивалентни, ако имат едни и същи корени.
Можем да получим еквивалентно уравнение, като:

• прибавим или извадим едно и също число от двете страни;
• умножим или разделим двете страни на уравнението на едно и също ненулево число.

⚠️ Важно: Ако умножим или разделим двете страни на уравнението с нула то губи смисъл, защото делението на нула е невъзможно.

1.4. Уравнения с дробни коефициенти

Уравнение с дробни коефициенти е уравнение, в което някои от коефициентите са дроби.
Например:

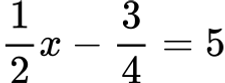
или

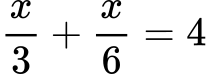
1.5. Основна идея при решаване

Целта ни е да се освободим от дробите, като направим уравнението по-удобно за решаване.
За целта:

👉 Намираме най-малкото общо кратно (НОК) на всички знаменатели в уравнението.
👉 Умножаваме двете страни на уравнението по това НОК.
👉 Така всички знаменатели „изчезват“, защото се съкращават.

👉 Получаваме еквивалентно уравнение с цели коефициенти.

👉След това решаваме полученото линейно уравнение.

Последователността от еквивалентни преобразувание се нарича освобождаване на уравнението от знаменател.

2. Примери и решения

Пример 1:

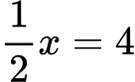
Решение:
Умножаваме двете страни по 2:

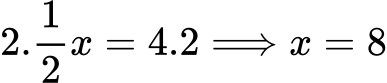
Проверка:
1/2 ⋅ 8 = 4 → вярно ✅
Отговор: x = 8

Пример 2:

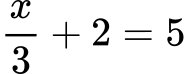
Решение:

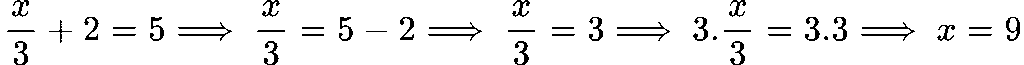
Отговор: x = 9

Пример 3:

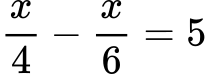
Решение:

НОК(4,6) = 12
Умножаваме двете страни на уравнението по 12:

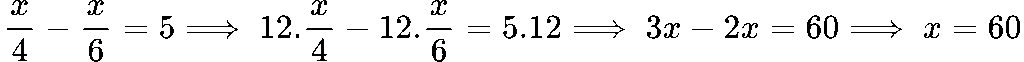
Отговор: x = 60

Пример 4:

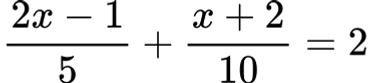
Решение:

НОК(5,10) = 10
Умножаваме двете страни на уравнението по 10:

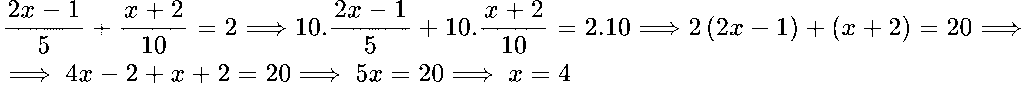
Отговор: x = 4

Пример 5:

(3x−2)/4 = (x+1)/2

НОК(4,2) = 4
Умножаваме по 4: 3x−2 = 2(x+1) ⇒ 3x − 2 = 2x + 2 ⇒ x = 4

Отговор: x = 4

3. Практически съвети

💡 Когато уравнението съдържа дроби с променливи в знаменателя (напр. 1/x), тогава първо намираме ОДС (област на допустимите стойности) – за кои стойности изразът има смисъл.

💡 Запомни, ако имаш отрицателно число в знаменателя, трябва да умножиш числителя и знаменателя на дробта по -1. Знакът “-” пред числителя или знаменателя на една дроб може да се премести пред дробната черта.

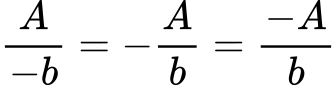
💡 Винаги проверявай решението си, като заместиш намереното x обратно в уравнението.

4. Заключение

Уравненията с дробни коефициенти може в началото да изглеждат „страшни“, но те просто изискват малко търпение и внимание.
След като премахнем знаменателите, уравнението се превръща в съвсем обикновено — точно като тези, които вече умееш да решаваш!

Помни:

„В математиката няма магия — има логика и последователност!“ 🧠