Здравейте, ученици! Днес ще се научим на умножение и деление на обикновени дроби. Тези умения са важни, защото ще ги използваме не само в математиката, но и в реалния живот. Ще разгледаме как се извършват тези операции и ще ви дадем примери и задачи, за да упражните наученото.

1. Теоретична част

1.1. Умножение на естествено число с обикновена дроб

Умножаваме едно естествено число с обикновена дроб, като го умножим с числителя на дадената дроб, а знаменателят се запазва същия.

Като равенство, това правило може да бъде записано по следния начин:

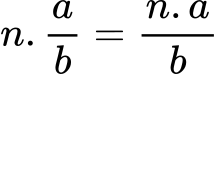
Например:

Ако имаме да извършим умножението на 5 с 2/7, то се получава следното:

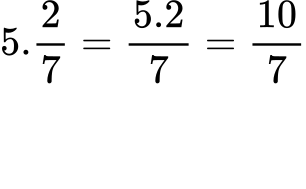
1.2. Умножение на обикновени дроби

Умножението на обикновени дроби е много просто. Просто умножаваме числителите и знаменателите на дробите поотделно. Следваме следната последователност от действия:

1. Умножаваме числителите и резултатът записваме като числител.
2. Умножаваме знаменателите и записваме произведението като знаменател.

Правилото може да бъде записано буквено по следния начин:

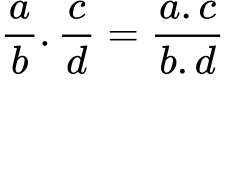
Например:

Ако трябва да умножим дробите 4/5 и 7/8, можем да запишем следното:

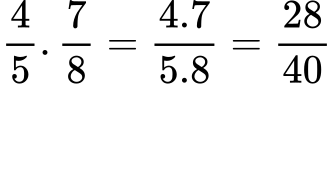
1.3. Що е то реципрочно число?

Реципрочните числа имат важна роля в аритметиката и алгебрата, особено при операциите с обикновени дроби. Те ни помагат за опростяване на изчисленията и имат ключова място в математиката.

Казваме, че реципрочното число на едно число a е числото, което след като се умножи с a, дава произведение равно на 1. С други думи, реципрочното число на a е 1/a​.

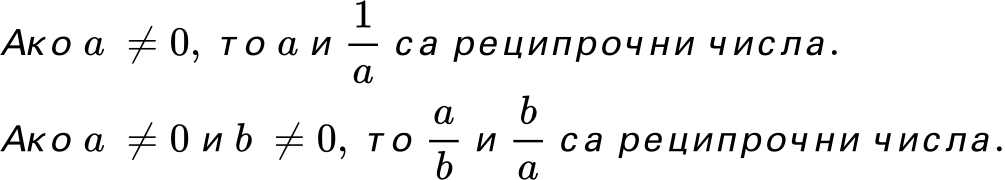
Например:

1.3.1. Защо реципрочните числа са полезни?

Реципрочните числа са особено полезни при деление на дроби. За да разделим една дроб на друга, умножаваме първата дроб по реципрочното число на втората дроб. Но това ще научиш подробно как се прави в следващата точка.

Произведението на две реципрочни числа винаги е равно на 1, или това може да се запише като:

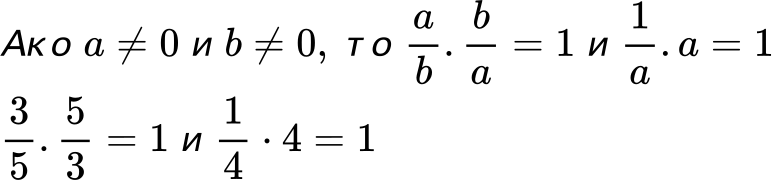
Запомни, че:

1. Числото 1 съвпада със своето реципрочно число т.к. 1.1/1 = 1
2. Числото 0 няма реципрочно число т.к. 0.a ≠ 1

1.4. Деление на обикновени дроби

При делението на дроби използваме метода “умножение с реципрочно число” (реципрочно число означава обръщане на дробта, като числителят и знаменателят си разменят местата). За да разделим дроби, умножаваме първата дроб по реципрочното число на втората дроб.

Записваме така:

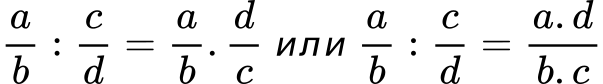
Например, ако имаме да извършим деление на обикновените дроби 7/8 : 4/9, можем да запишем решението по следния начин:

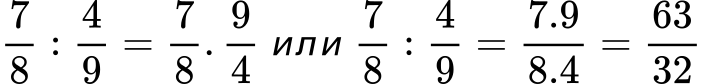
2. Изчислителни задачи

1. Умножете следните дроби:

a)

Решение:

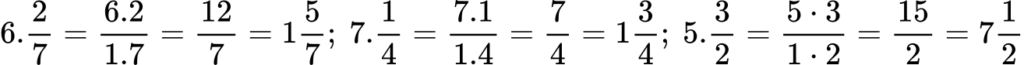
б)

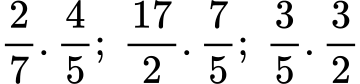
Решение:

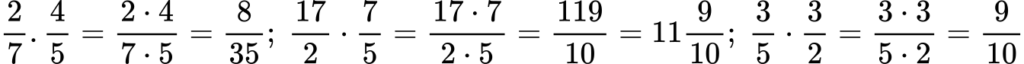
в) ​

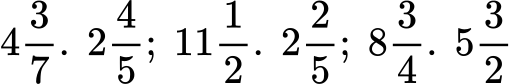
Решение:

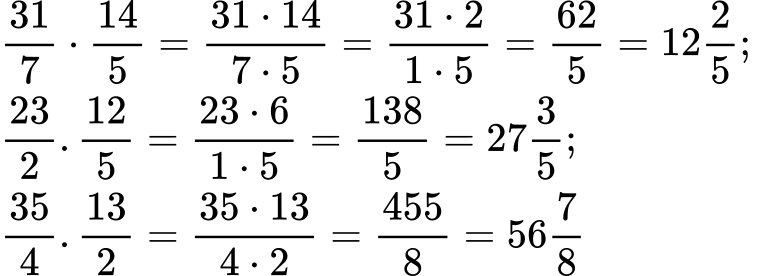
2. Разделете следните дроби:

а)

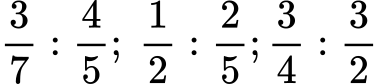
Решение:

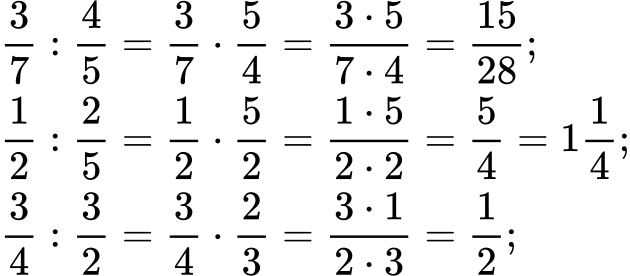
б)

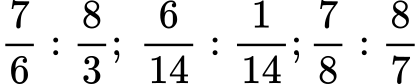
Решение:

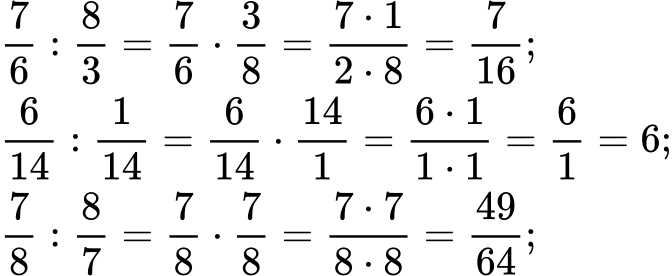
в)

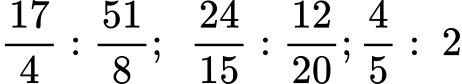
Решение:

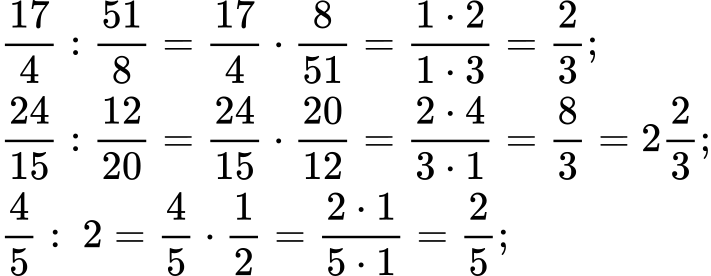
3. Текстови задачи

1. Правоъгълник има страни 4 2/3 cm и 3 1/3 cm. Намерете лицето му.

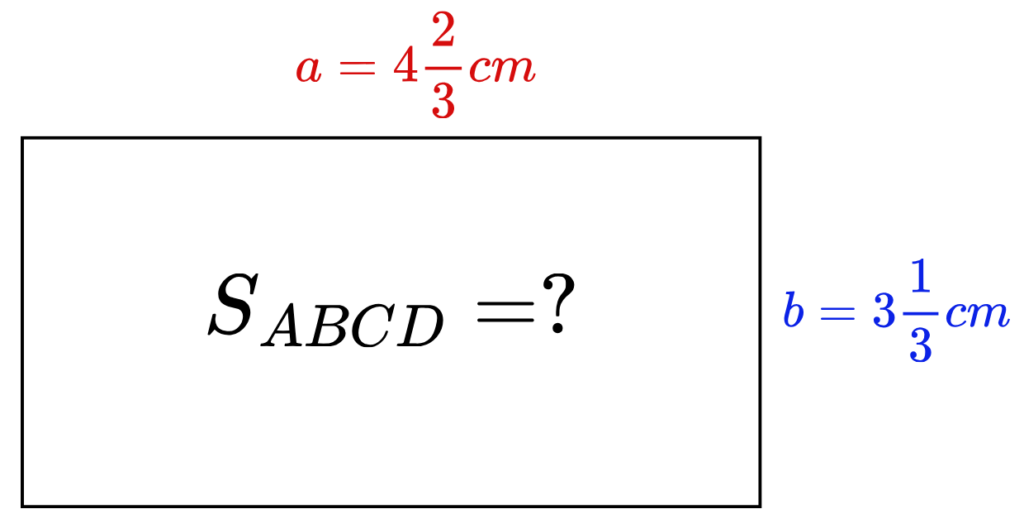
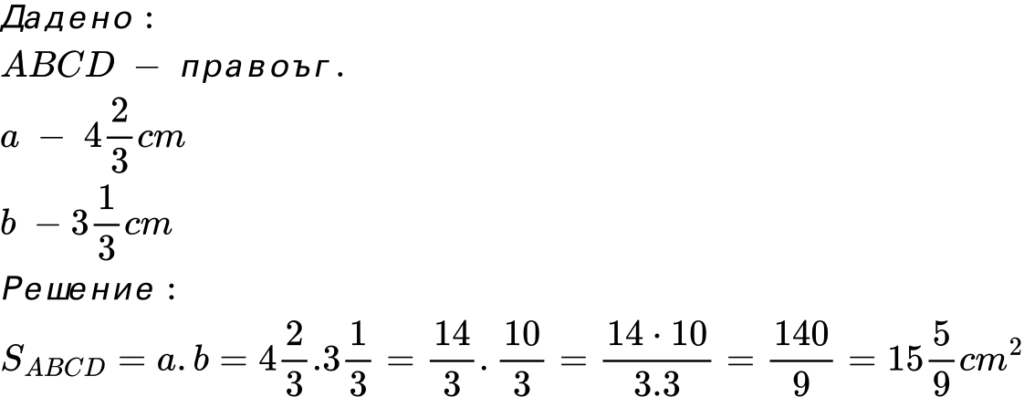
2. Един заек изяжда дневно 1/3 kg люцерна, а една крава 7 пъти повече. Колко люцерна изяжда дневно кравата?

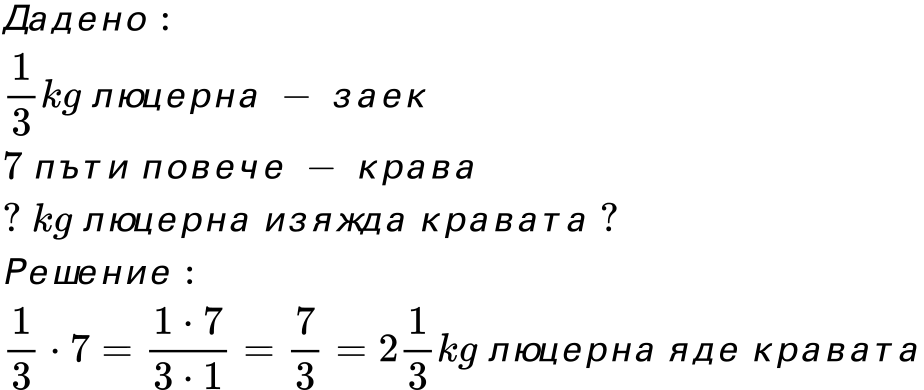
4. Практически задачи

1. За партито на Ради майка му решила да приготви напитка, която съдържала по 1/2 чаша от 9 различни сиропа. Колко чаши ще може да направи майката на Ради с половината от тази напитка?

2. Какъв път ще измине един гепард, ако за 4 3/4 min се движи със скорост 2 3/5 m/min?

3. Моторист се движи 2 1/8 часа със скорост 80 километра в час. Какво разстояние е изминал мотористът?

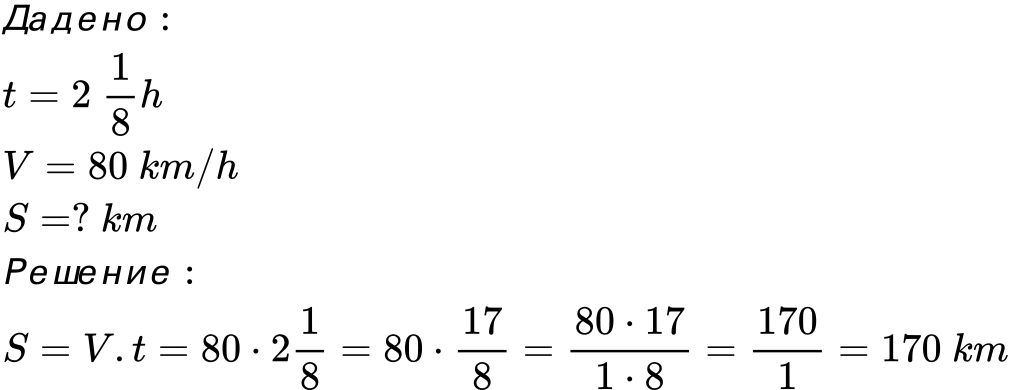
4. Квадрат има страна 4/5 m, а правоъгълник страни 2/3 m и 1/5 m. Коя от двете фигури има по-голямо лице и с колко то е по-голямо?

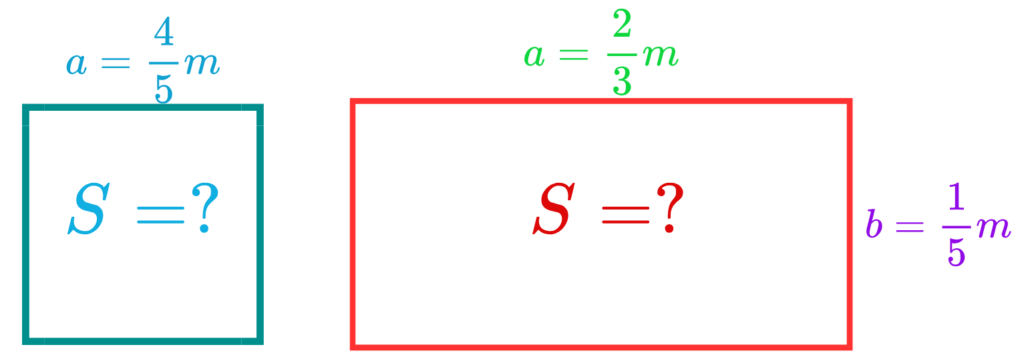
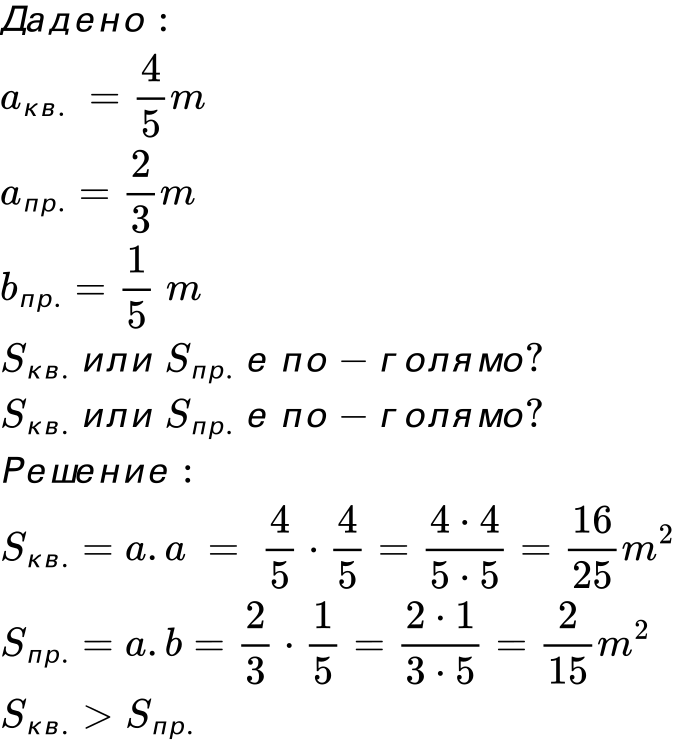
5. Заключение

Умножението и делението на дроби са полезни умения, които често се използват в ежедневието. Независимо дали при готвене, четене или решаване на задачи, дробите са навсякъде около нас. Важно е да упражняваме тези умения, за да ги овладеем добре и да ги използваме с лекота.