Умножение и деление на рационални числа
Здравейте, шестокласници! Време е да се научим да извършваме още две действия с положителни и отрицателни числа. Днес ще разгледаме темите за умножение и деление на рационални числа.

С днешния урок завършваме правилата за действия с рационални числа и сме готови да решаваме изрази с всички изучени дотук действия! Знанията са като листата на дърво- колкото повече научаваме, толкова по красиво и кичесто става нашето дърво на уменията ни!
Умножение на рационални числа
Правилото за умножение на две рационални числа е много, много просто! Единствено трябва да съобразим дали двете числа са с еднакви или с различни знаци.
Хайде да видим следващите четири примера и да изведем заедно правилото.
—5.5,2 = — 26 5.(—5,2) = —26
5.5,2 = 26 —5.(—5,2) = 26
Забеляза ли вече общото между примерите? Произведението се различава само по знака, а той се определя от това дали множителите са с еднакви или различни знаци.

Когато умножаваме две рационални числа първо определяме знака на произведението, след това умножаваме модулите на числата.
Произведението на две рационални числа с еднакви знаци е положително число, а на две рационални числа с различни знаци-отрицателно число.
А сега да се упражним с два примера!
2 3/4 . (— 0,5) и —2,2.(—1/2)
Първо определяме знакът на произведението, за да сме сигурни, че няма да го забравим след това.
Множителите на първото произведение са с различни знаци, тъй като едното е положително число, а другото — отрицателно. Произведението ще бъде отрицателно число, остава само да умножим модулите на числата.
2 3/4 . (— 0,5) = — (2,75.0,5) = —1,375
Множителите на второто произведение са с еднакви знаци, двете са отрицателни числа, затова произведението ще бъде положително число. Вече помните, че знакът + пред положително число може да се пропуска в началото на израза или след знакът за равенство.
—2,2.(—1/2) = +(2,2.0,5) = 1,1
Деление на рационални числа
Може би си спомняте от пети клас, че частното на две числа можем да запишем като произведение на делимото с реципрочното число на делителя. Например:
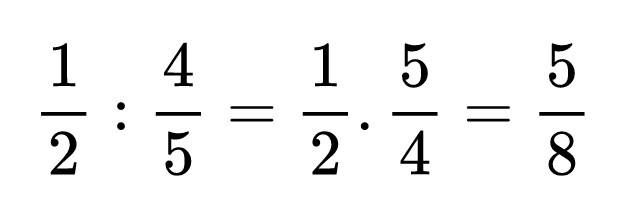
Това правило ни върши страхотна работа, тъй като всяко частно на две числа можем да запишем като произведение! Ами тогава при делението на рационалните числа ще използваме правилото за умножение на рационални числа!
Когато делим две рационални числа първо определяме знака на частното, след това разделяме модулите на делимото и делителя.
Частното на две рационални числа с еднакви знаци е положително число, а на две рационални числа с различни знаци-отрицателно число.
Хайде да решим две задачи с деление на рационални числа.
2,5:(—0,5) и —15,35:(—1/2)
Отново определяме първо какъв знак има частното и след това делим модулите на делимото и делителя. В първата задача двете числа са с различни знаци и ще получим отрицателно частно. След това трябва да умножим делимото и делителя с 10, за да делим на цяло число. Получаваме:
2,5:(—0,5) = —(25:5)= —5
Във втория пример двете числа са отрицателни, затова частното ще е положително число. Тъй като делим на обикновена дроб, трябва да представим делението като умножение на делимото с реципрочното число на делителя.
—15,35:(—1/2) = +(15,35.2) = 30,7
Произведение на повече от две рационални числа
Много често ще срещате изрази, в които множителите са повече от два. За да определим знака на произведението е достатъчно да преброим колко са отрицателните множители. Ако те са четен брой, то произведението ще е положително число, защото произведението на всяка двойка отрицателни числа е положително число. Като използваме съдружителното свойство получаваме:
—5.(—7,2). (—2).(—0,5)=
=(—5.(—7,2)).((—2).(—0,5)) =
= + 36.(+1) = 36
Да видим сега един пример с нечетен брой отрицателни множители:
—5.(—7,2). (—2) =
= (—5.(—7,2)).(—2) =
= +36.(—2) = —72

Когато броят на отрицателните множители е четно число, то произведението ще е положително число.
Ако броят на отрицателните множители е нечетно число, то произведението ще е отрицателно число.
Ред на действие при изрази с рационални числа
Хубавото е, че когато пресмятаме изрази с рационални числа, спазваме същият ред на действие, който вече познаваме от предишните години. Можеш да си го припомниш в тази статия:
Намиране на неизвестно число. Ред на действие при изчисляване.
Да видим как ще го прилагаме, когато изразите са с положителни и отрицателни числа.
—1,25:(—1/4)+0,5.(—0,06)
Тук първо трябва да извършим делението и умножението и чак след това ще съберем получените частно и произведение:
—1,25:(—1/4)+0,5.(—0,06) =
= +(1,25:0,25)+(—0,5.0,06)=
=125:25 + (—0,03) =
= 5 + (—0,03) = 4,97

Внимавай да не объркаш правилата за събиране и изваждане на рационални числа с тези за умножение и деление!
Ето тук можеш да си припомниш как се събират и изваждат рационални числа:
Хайде да решим следващата задача:
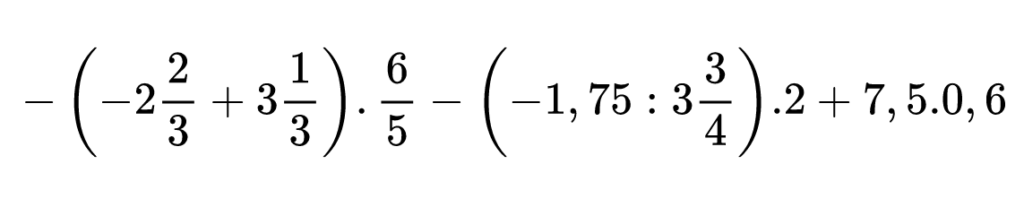
Тук първо извършваме действията в двете скоби, а извън тях можем да пресметнем произведението в края на израза:
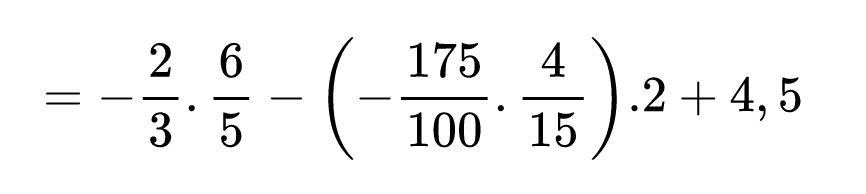
Обърна ли внимание, че знакът минус пред първите скоби промени знакът на полученият сбор? Във вторите скоби записахме делимото като десетична дроб, а делителят записан като неправилна дроб е 15/4, затова умножаваме с реципрочното му число 4/15.
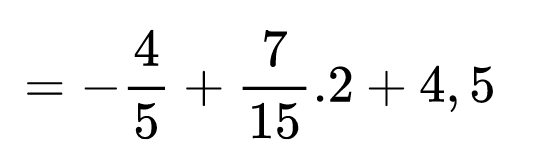
След умножението на обикновените дроби получаваме горния израз. Минусът пред вторите скоби отново смени знакът на полученото произведение. След това остава да пресметнем последното произведение в израза:
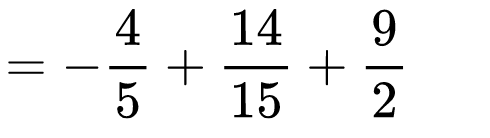
Записахме 4,5 като обикновена дроб. Вижда се, че дробите са с различни знаменатели. НОК на трите знаменателя е числото 30. Разширяваме дробите последователно с допълнителни множители 6, 2 и 15.
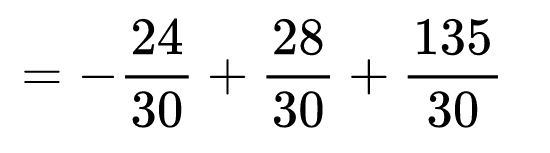
Остава само съберем трите числа. Може да се комбинират двете положителни числа и след това да се прибави отрицателното или да пресмятаме подред:


Време е да се упражниш като решиш следващия тест!