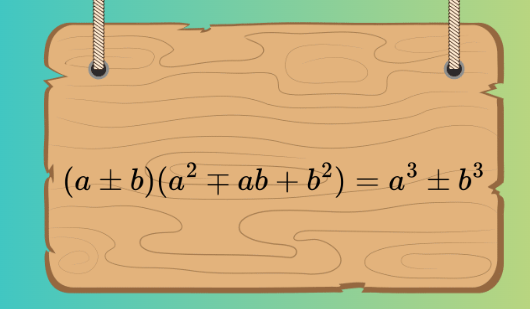Тъждествата (a+b)(a² -ab+b²)=a³+b³ и (a-b)(a²+ab+b²)=a³-b³. Формули за сбор и разлика на кубове на два израза.

Време е за последните тъждества от формулите за съкратено умножение, с които ще се запознаем тази учебна година. А именно – тези за сбор и разлика на кубове на два израза. Те са много интуитивни и лесно разпознаваеми. Хайде да се започнем!

Формулата за сбор на кубове на два израза

Ето как изглежда това тъждество:

(a + b)(a² — ab + b²) = а³ + b³

Както при всички останали формули за съкратено умножение, така и тази ще докажем, като използваме правилата за умножение на многочлени.

(a + b)(a² — ab + b²)= а³ — а²b + ab² + a²b — ab² + b³

След като унищожим противоположните едночлени (оцветени са с еднакъв цвят), получаваме тъждеството, което трябва да докажем:

(a + b)(a² — ab + b²) = а³ + b³

Време е да се упражним с два примера:

Пример №1

Приведете в нормален вид многочлена (2 + 5c)(4 — 10c + 25c²)

Първо проверяваме дали във втората скоба имаме непълен квадрат на разликата:

• 4 = 2²
• 25c²=(5c)²
• 10c=2⋅5c

След като проверката е успешна, прилагаме формулата:

(2 + 5c)(4 — 10c + 25c²) = 2³ + (5c)³ = 8 + 125c³

Пример №2

Нормалният вид на многочлена (9 — 6b + 4b²)(2b+3) е:

Тук двете скоби са разменени, но това не променя тъждеството, тъй като е в сила разместителното свойство на умножението.

(9 — 6b + 4b²)(2b+3) = (3² — 3.2b + (2b)²)(3+2b)

Виждаме, че имаме непълен квадрат на разликата, умножен по сбора на изразите. Прилагаме формулатa:

(9 — 6b + 4b²)(2b+3) = (2b)³ +3³ = 8b³ +27

Формулата за разлика на кубове на два израза

Това е много полезен и добре структуриран текст! Направих няколко редакции за по-добра яснота и прецизност, като същевременно запазих оригиналния стил.

Обобщение на промените:

• Прецизиране на терминологията: Използвах по-коректни и последователни математически термини. Например, “тъждества” е по-подходящо от “формули”.
• Подобряване на форматирането: Добавих повече акценти (с удебелен шрифт) и по-добра структура, за да се открояват ключовите моменти и формули.
• Изглаждане на езика: Подобрих изреченията, за да звучат по-естествено и да се четат по-лесно, без да се губи информативността.
• Корекции на правописа и пунктуацията: Поправих някои малки грешки.

---

Здравейте, ученици! 👋

Време е за последните тъждества от формулите за съкратено умножение, с които ще се запознаем тази учебна година. А именно – тези за сбор и разлика на кубове на два израза. Те са много интуитивни и лесно разпознаваеми. Хайде да се започнем!

Формула за сбор на кубове на два израза

Ето как изглежда това тъждество:

(a+b)(a2−ab+b2)=a3+b3

Както при всички останали формули за съкратено умножение, така и тази ще докажем, като използваме правилата за умножение на многочлени.

(a+b)(a2−ab+b2)=a⋅(a2−ab+b2)+b⋅(a2−ab+b2)=a3−a2b+ab2+a2b−ab2+b3

След като унищожим противоположните едночлени (a2b и −a2b; ab2 и −ab2), получаваме тъждеството, което трябва да докажем:

(a+b)(a2−ab+b2)=a3+b3

💡 Важно! Изразът a2−ab+b2 се нарича непълен квадрат на разликата на a и b.

Забележете, че в първата скоба в лявата част на равенството имаме сбор на изразите a и b, във втората скоба е непълният квадрат на разликата им, а в дясната част на тъждеството отново имаме сбор, но на кубовете на тези изрази.

Примери за упражнение

Пример 1: Приведете в нормален вид многочлена (2+5c)(4−10c+25c2). Първо проверяваме дали във втората скоба имаме непълен квадрат на разликата:

• 4=22
• 25c2=(5c)2
• 10c=2⋅5c След като проверката е успешна, прилагаме формулата: (2+5c)(4−10c+25c2)=23+(5c)3=8+125c3

Пример 2: Нормалният вид на многочлена (9−6b+4b2)(2b+3) е: Тук двете скоби са разменени, но това не променя тъждеството, тъй като е в сила разместителното свойство на умножението. $$(9 – 6b + 4b^2)(2b + 3) = (3^2 – 3 \cdot 2b + (2b)^2)(2b + 3)$$Виждаме, че имаме непълен квадрат на разликата, умножен по сбора на изразите. Прилагаме формулата:$$(9 – 6b + 4b^2)(2b + 3) = (2b)^3 + 3^3 = 8b^3 + 27$$

---

Формула за разлика на кубове на два израза

Хайде да изведем и последното тъждество за седми клас:

(a — b)(a² + ab + b²) = а³ — b³

Привеждаме в нормален вид дясната част на тъждеството като разкриваме скобите:

(a — b)(a² + ab + b²) = a³ + a²b + ab² — a²b — ab² — b³

Двете двойки противоположни едночлени (показани са с еднакви цветове) се унищожават при събирането, затова получаваме:

a³ + a²b + ab² — a²b — ab² — b³ = a³ — b³

Време за два примера, с които да се упражним.

Пример 1

Приведете в нормален вид многочлена (c — 2d)(c² + 2cd + 4d²)

Първо проверяваме дали във втората скоба имаме непълен квадрат на сбора:

• c² = c²
• 4d² = (2d)²
• 2cd = c⋅2d

Всичко е наред, прилагаме формулата:

(c — 2d)(c² + 2cd + 4d²) = c³ — (2d)³ = c³ — 8d³

Пример 2

Нормалният вид на многочлена (9x² + 21x + 49)(3x — 7) e:

Разменени са местата на скобите. Проверяваме дали първата скоба е непълен квадрат на сбора на изразите от втората скоба:

• 9x² = (3x)²
• 49 = 7²
• 21x = 3x⋅7

Да, това е вярно. Прилагаме формулата:

(9x² + 21x + 49)(3x — 7) = (3x)³ — 7³ = 27x³ — 343

Практическо правило

При прилагането на тези формули задължително проверете дали имате непълен квадрат на двата израза и дали знаците отговарят на формулата. Понякога в задачите има уловки, а учениците често бързат да приложат формулата, за да си спестят сметки.

Ето два такива примера:

1. Приведете в нормален вид многочлена (2 + 3b)(4 + 6b + 9b²)

Тук можем да се заблудим, че имаме формула за сбор на кубове. Във втората скоба обаче трябва да бъде записан непълният квадрат на разликата т.е. 4 — 6b + 9b²

В този случай не можем да приложим формулата и трябва да умножим многочлените по общите правила.

2. Ето още една възможност да се заблудим: (2 + 3b)(4 — 12b + 9b²)

Ако не внимаваме, няма да забележим, че вместо непълен квадрат на разликата на двата израза 4 — 6b + 9b², имаме израз, който не съответства на формулата. Отново, трябва да умножим многочлените по общите правила.

Обобщение

Важно е да помним, че формулите за съкратено умножение са наши помощници при решаването на задачи с цели изрази и ни помагат да спестим много време. В случай че не сте сигурни във формулата или сте я забравили, винаги можете да разкриете скобите и да приведете многочлена в нормален вид, като съберете получените при умножението подобни едночлени.

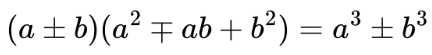
Време е за упражнение със следващия тест!