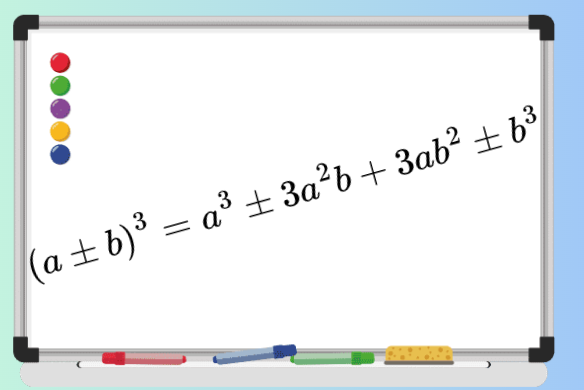Тъждествата (a+b)3=a3+3a2b+3ab2+b3 и (a-b)3=a3-3a2b+3ab2-b3. Формулите за куб на сбор и куб на разлика на два израза
Здравейте, седмокласници! Време е да се запознаем с две нови тъждества, които също имат много интересни имена – формулите за куб на сбор и куб на разлика. Когато ги използваме, все едно нареждаме пъзел, всеки знак и степен си имат специално място. Хайде да се запознаем с тях!
Формулата за куб на сбор на два израза
Може би вече се досещате, че тук ще имаме сбор, който е на трета степен (оттам произлиза “куб” на сбор). Хайде да изведем заедно тъждеството и след това да обърнем внимание на някои специални степенни показатели и множители!
Нека приведем в нормален вид (a + b)3 . За целта първо го представяме като произведение на три множителя.
(a + b)3 = (a + b).(a + b).(a + b)
Нека умножим първите две скоби като използваме формулата за квадрат на сбор:
(a + b).(a + b).(a + b)= (а2 + 2ab + b2).(a + b)
А сега да довършим тъждествените преобразувания като умножим двете скоби по правилото за умножение на многочлени.
(а2 + 2ab + b2).(a + b) = а3 + а2b + 2а2b + 2ab2 + ab2 + b3
Остана да съберем подобните едночлени (оцветени са с еднакви цветове).
а3 +а2b + 2а2b + 2ab2 + ab2 + b3 = а3 +3а2b + 3ab2 + b3
Нека обобщим тъждеството!
(a + b)3 = а3 + 3а2b + 3ab2 + b3

Забележете как се премества тройката от степенния показател в тъждеството- първо е степенен показател на първия израз, след това е множител пред двете произведения и накрая отново е в степенен показател.
(a + b)3 = а3 + 3а2b + 3ab2 + b3
Също е важно да забележите как в едното произведение първият израз е на втора степен, а в другото произведение- вторият израз:
(a + b)3 = а3 + 3а2b + 3ab2 + b3
Пример 1:
Запишете в нормален вид (3x + 1)2
Прилагаме директно формулата:
(3x + 1)3 = (3x)3 + 3.(3x)2.1 + 3.3x.12 + 13 = 27x3 + 27x2 + 9x + 1
Пример 2:
(0,1x + 3y)3 = (0,1x)3 + 3.(0,1x)2.3y + 3.0,1x.(3y)2 + (3y)3 = 0,001x3 + 0,09x2y + 2,7xy2 + 27y3
Формулата за куб на разлика на два израза
За да докажем тази формула, ще преминем през същите стъпки:
(a — b)3 = (a — b).(a — b).(a — b)
Нека умножим първите две скоби като използваме формулата за квадрат на разлика:
(a — b).(a — b).(a — b)= (а2 — 2ab + b2).(a — b)
Умножаваме двата многочлена:
(а2 — 2ab + b2).(a —b) = а3 — а2b — 2а2b + 2ab2 + ab2 — b3
Събираме подобните едночлени (оцветени са с еднакви цветове).
а3 — а2b — 2а2b + 2ab2 + ab2 — b3 = а3 — 3а2b + 3ab2 — b3
Нека обобщим тъждеството!
(a — b)3 = а3 — 3а2b + 3ab2 — b3

Да обърнем внимание на различията между двете формули! Вижте как при формулата за куб на разлика се редуват знаците в дясната част на тъждеството (+ ; — ; + ; —).
(a — b)3 = + а3 — 3а2b + 3ab2 — b3
Минусът е пред нечетната степен на b.
Време е за упражнение:
Пример №3
Представете в нормален вид многочлена:
(2x — 5)3 = (2x)3 — 3.(2x)2.5 + 3.2x.52 — 53 = 8x3 — 60x2 + 150x — 125
Пример №4
Докажете тъждеството:
(3x — 0,3y)3 = 27x3 — 8,1x2y + 0,81xy2 — 0,027y3
Прилагаме формулата за куб на разлика на два израза за лявата част на равенството:
(3x — 0,3y)3 = (3x)3 — 3.(3x)2.0,3y + 3.3x.(0,3y)2 — (0,3y)3 = 27x3 — 8,1x2y + 0,81xy2 — 0,027y3
Получихме същия израз като в дясната страна на равенството, с което доказахме тъждеството.

Важно е да отбележим, че при тези две формули често се допуска грешка, когато се спестява подробното описание. По-добре да направим няколко допълнителнителни записа, за да не сгрешим задачата.
Двете формули можем да запишем заедно с една обща формула:
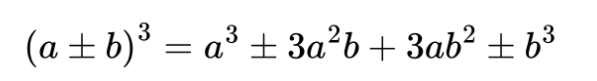
Практическо правило
А сега дойде ред на много полезно правило. Да разгледаме ето този многочлен: (—a — b)3
Имаме два минуса в скобите и това може да ни затрудни при прилагане на формулата. Затова можем в скобите да изнесем —1 като общ множител:
(—a — b)3 = (—1.(a + b))3
Сега прилагаме правилото за степенуване на произведение и повдигаме на трета степен (—1) и (a + b).
(—1.(a + b))3 = (—1)3.(a + b)3 = —1.(a + b)3 = — (a + b)3
Нека обобщим:
(—a — b)3 = — (a + b)3

Ако искаме да сменим знаците пред двата израза във формулата за куб на сбор или куб на разлика, трябва да изнесем минус пред скобите.
(—a — b)3 = — (a + b)3
(—a + b)3 = — (a — b)3
Обобщение:
Формулите за куб на сбор и куб на разлика изискват внимателни изчисления, затова е добре да не спестяваме от описанието им. Трябва да внимаваме за степенните показатели, както и за редуването на знаците при формулата за куб на разлика. С добра концентрация няма да имате никакви проблеми с тези две тъждества!
А сега е време за упражнение!