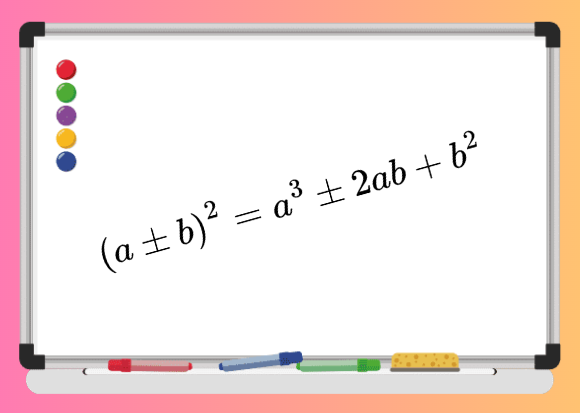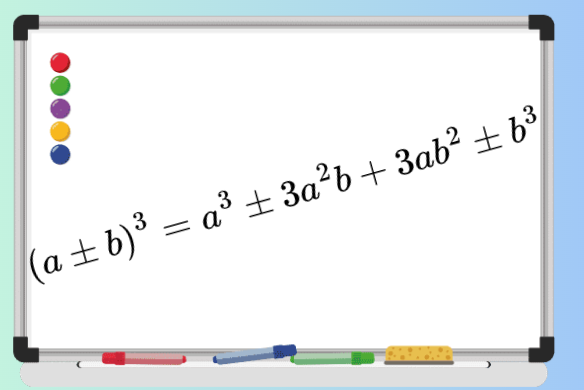Тъждествата (a+b)2=а2+2ab+b2 и (a-b)2=a2-2ab+b2. Формулите за квадрат на сбор и квадрат на разлика на два израза.
Здравейте, седмокласници! Днес ще разгадаем какво представляват формулите за съкратено умножение и защо се използват. Днес ще се запознаем с едни от най-често използваните – формулите за квадрат на сбор и квадрат на разлика на два израза. Те ще ви бъдат полезни, докато завършите целия училищен курс по математика!
Какво представляват формулите за съкратено умножние
Името на тези формули не е случайно! То подсказва, че с тях ще спестим много време, като умножаваме по-бързо.Възможно е да се запитате: “Ами ако забравя формулата?” Няма проблем! Просто ще приложите правилото за умножение на многочлени, но ще ви отнеме малко повече време. Затова е добре да ги научите наизуст!
Формулата за квадрат на сбор на два израза или тъждеството (a+b)2 = a2 + 2ab + b2
Нека първо се убедим, че тази формула работи!
Можем да представим (a + b)2 като произведение на множители:
(a + b)2 = (a + b).(a + b)
Хайде сега да използваме правилото за умножение на многочлени, като умножим всеки от едночлените в първите скоби последователно с всеки от едночлените във вторите скоби.
(a + b)2 = (a + b).(a + b) = а2 + ab + ab + b2
A сега да приведем в нормален вид многочлена като съберем двата подобни едночлена. Получаваме:
а2 + ab + ab + b2 = а2 + 2ab + b2
Нека обобщим крайния резултат:
(a+b)2 = а2 + 2ab + b2

Сборът на два израза, повдигнат на втора степен, е равен на квадрата на първия израз плюс удвоеното им произведение плюс квадрата на втория израз.
(a + b)2 = а2 + 2ab + b2
Пример №1
Нека да представим в нормален вид многочлена (2x + 3)2 , като използваме формулата за квадрат на сбор на два израза. Използваме формулата за квадрат на сбор на два израза. Записваме квадрата на първия едночлен, който е (2x)2. След това прибавяме удвоеното произведение на двата едночлена, което е 2⋅2x⋅3. Накрая прибавяме квадрата на втория едночлен, който е 32.
(2x + 3)2 = (2x)2 + 2.2x.3 + 32
Остава да приведем в нормален вид многочлена:
(2x + 3)2 = (2x)2 + 2.2x.3 + 32 = 4x2 + 12x + 9

С повече упражнения, ще можете да пресмятате квадратите на изразите и тяхното удвоено произведение много по-бързо, прескачайки подробните стъпки
Пример №2
Нека разгледаме още един пример:
(4x2 + 8y3)2 = (4x2)2 + 2.4x2.8y3 + (8y3)2 = 16x4 + 64x2y3 + 64y6
Тук на помощ ни идват правилата от степенуването! Ако сте ги забравили, върнете се да си ги припомните от секцията 6.клас.
Формулата за квадрат на разлика на два израза или тъждеството (a – b)2 = a2 – 2ab + b2
Може би вече се досещате, че отново ще изведем формулата като използваме правилото за умножение на многочлени.
(a — b)2 = (a — b).(a — b) = а2 — ab — ab + b2 = а2 — 2ab + b2
Накратко:
(a — b)2 = а2 — 2ab + b2

Разликата на два израза, повдигната на втора степен, е равна на квадрата на първия израз минус удвоеното им произведение плюс квадрата на втория израз.
(a — b)2 = а2 — 2ab + b2
Пример №1
Приведете в нормален вид (5y — 10)2 .
Използваме формулата за квадрат на разликата на два израза:
(5y — 10)2 = (5y)2 —2.5y.10 + 102 = 25y2 — 100y + 100.
Разликата между тъждествата за квадрат на сбор и квадрат на разлика е единствено, че при квадрата на разликата трябва да извадим удвоеното произведение.
(a + b)2 = а2 + 2ab + b2
(a — b)2 = а2 — 2ab + b2
Пример №2
Представете в нормален вид:
(7x4 — 2y5)2 = (7x4)2 — 2.7x4.2y5 + (2y5)2 = 49x8 — 28x4y5 + 4y10
Обща формула за квадрат на сбор и квадрат на разлика на два израза
Деца, математиците често обединяват две формули в една. Това не само спестява изписването им поотделно, но и подчертава малките разлики между тях. Тъй като при формулите от днешния урок разликите са много малки, можем да ги обединим в следната формула:
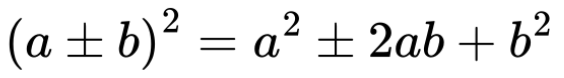
Тук трябва много да внимаваме със знаците! Когато отляво вземем горния знак (плюс), отдясно също трябва да вземем горния знак (плюс). Не можем да вземем горния знак отляво и долния знак отдясно!
Виждате ли колко е удобно това? Математиката е пълна с такива умни решения!
Практическо правило:
Време е за много полезно правило. Да разгледаме ето този многочлен: (—a — b)2
Имаме два минуса в скобите и това може да ни обърка при прилагане на формулата. Затова можем в скобите да изнесем —1 като общ множител:
(—a — b)2 = (—1.(a + b))2
Сега прилагаме правилото за степенуване на произведение и повдигаме на трета степен (—1) и (a + b).
(—1.(a + b))2 = (—1)2.(a + b)2 = 1.(a + b)2 = (a + b)2
Нека обобщим:
(—a — b)2 = (a + b)2

Можем да сменим знаците пред двата израза във формулите за квадрат на сбор и квадрат на разлика и това няма да промени тъждеството.
(—a — b)2 = (a + b)2
(а — b)2 = ( b — a)2
Заключение:
Най-важното е да запомните, че формулите за съкратено умножение ни спестяват много време. Вместо да умножаваме многочлени по общите правила, можем директно да ги прилагаме. Те са много полезни и ще ги използвате често в уроците по математика и в гимназията.
Време е да се упражниш със следващия тест!