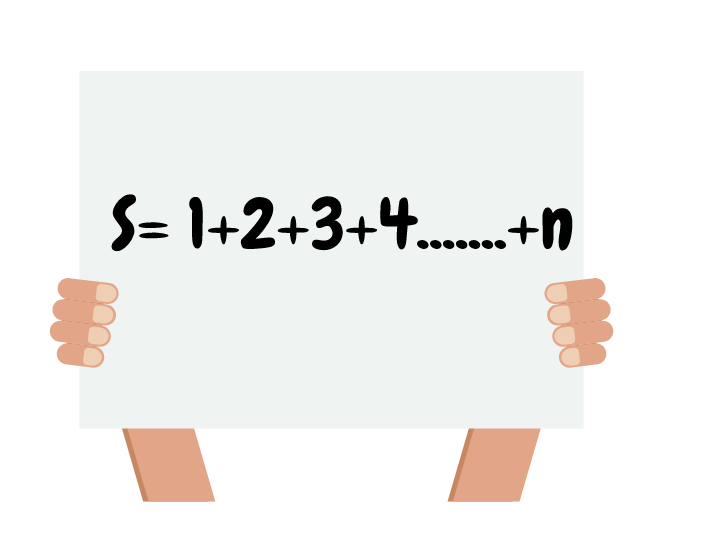Трикове при деление на многоцифрени числа

Здравейте, малки математици! Стигнахме до една много, много важна тема! А именно-трикове при деление на многоцифрени числа! Днес ще се научим на някои хитрини, с които да си помогнем 😉

Действие деление-съставни части

За да ни е по-лесно да запомняме правила, всяко едно число при действието деление си има специално (кодово) име! Хайде да ги припомним с ето това ревенство!

a:b=c

a-делимо, така наричаме числото, което делим.

b– делител, това е числото, на което разделяме делимото.

c– частно, това е числото, което получаваме като извършим делението.

Сега да припомним две много важни правила!

Ако умножим частното с делителя, ще получим делимото!

Така винаги можем да направим проверка на нашите изчисления.

Ако разделим делимото на частното, ще получим делителя!

Да видим как изглеждат тези правила, записани с числа:

60:12=5

5.12=60

60:5=12

Използваме ги и когато трябва да намерим неизвестно делимо или неизвестен делител.

За да се справим със задача с деление, задължително трябва да знаем перфектно таблицата за умножние и да умеем да умножаваме многоцифрени числа.

Някои трикове при делението на многоцифрени числа

• Трик №1:Когато броят на цифрите на делимото и делителят е равен,  частното винаги е едноцифрено число.

Например: 250:125=2

Делимото и делителят са трицифрени числа, затова резултатът е едноцифрено число.

• Трик №2: Когато броят на цифрите на делимото е повече от броя на цифрите в делителя и първата цифра на делителят е по-голяма от първата цифра на делимото, то броят на цифрите в частното е равен на разликата на броя на цифрите в делимото и делителя.

Например:

1250:25=50

В този пример делимото е четирицифрено число, а делителят е двуцифрено число. Първата цифра на делителя е 2 и е по-голяма от първата цифра на делимото, която е 1. Затова броят на цифрите в частното намираме така: 4-2=2. Наистина числото 50 се записва с две цифри!

• Трик №3: Когато броят на цифрите на делимото са повече от броят на цифрите в делителя, но първата цифра на делителят е по-малка от първата цифра на делимото, то тогава към разликата на броят на цифрите им трябва да добавим 1.

Например:

6025:25=241

Тук делимото е читирицифрено число, а делителят е двуцифрено число. В този пример обаче първата цифра на делимото е по-голяма от първата цифра на делителя (6>2), затова броят на цифрите на частното ще получим ето така: (4-2)+1=3

Може би се чудиш къде ще са ти полезни тези трикове? Ами много често забравяме да добавим една нула в частното, когато сваляме две поредни числа от делимото.

Например 420:4=105. Много биха се объркали и записали, че частното е 15. С помощта на триковете лесно проверяваме дали не сме получили частно с по-малък брой цифри.

Намиране на близка стойност при деление на числа

Много ще ни е полезно да видим частното, което получаваме, до кое число ще е близко или дори от кое е по-голямо или по-малко. Така можем също да си хванем някоя изчислителна грешка!

Да видим един пример:

1600:25=?

Със сигурност ще ми е много лесно да пресметна 1600:20. Можем да делим 160 на 2, тъй като двете числа се делят на 10. Получава се 80. Но в нашия пример делителят е по-голямо число. Веднага може да кажем, че частното ще е по-малко от 80!

Можем да пресметнем и до кое число е близко частното на 1600 и 30. Махаме двете нули от делимото и делителя (тъй като се делят на 10 и можем да работим с по-малки числа) и остава 160:3.

Получава се остатък при делението, но най-близкото число е 53 (53.3=159).

Сега вече сме сигурни, че нашето частно попада между 53 и 80.

Да видим дали сме прави:

1600:25=64

Правило при търсене на подходящ множител на делителя

Случвало ли ти се е да губиш страшно много време, за да намериш точно колко пъти се събира твоя делител в определено число?

Да видим дали не можем да се научим да пестим време!

Да разгледаме ето този пример:

374:17′?

Нека видим с колко цифри ще е изписано частното. Делимото е трицифрено число, а делителят е двуцифрено число, но първата цифра на делимото е по-голяма от първата цифра на делителя. Тогава частното ще е с (3-2)+1=2 цифри.

Проверяваме колко пъти се побира числото 17 в 37. Виждаме, че 37 е само с 20 по-голямо от 17. Веднага преценяваме, че ще се побере точно още веднъж. Затова най-близкият множител на 17, с който да получим подходящо число, е 2.

2.17=34.

Разликата на 37 и 34 е 3. След като свалим следващата цирфа от делимото, се получава точно 34. Веднага записваме, че 374:17=22

Проверка: 22.17=374

Още примери с прилагане на трикове за деление на многоцифрени числа

Да видим какво сме научили.Да проверим на какви условия ще отгваря частното на 296 и 37.

Първо да определим от колко цифри ще е съставено частното. Делимото е трицифрено число, а делителят е двуцифрено число. Първата цифра на делителя е по-голяма от тази на делимото (3>2). Затова частното ще има 3-2=1 цифра.

Тогава търсим едноцифрено число. Да опитаме да открием граници, в които попада това число, за да изчисляваме по-малко. 296 е много по-голямо от 37, затова е разумно да проверим на колко е равно произведението на 10 и 37. Получаваме 370. Разликата на 370 и 296 е 74. 37 се събира точно 2 пъти в 74, затова намаляваме с две единици 10 и получаваме:

296:37=8

Проверка 8.37=296

Да намерим частното на 6560 и 410 като използваме нашите трикове!

Първо виждаме, че и двете числа се делят на 10, защото завършват на нула. Тогава можем да махнем нулите в края им и да делим 656 на 41. Така ще работим с по-малки числа.

Сега да проверим с колко цифри ще се записва тяхното частно. Виждаме, че делимото е с повече цифри и неговата първа цифра е по-голяма от първата цифра на делителя (6>4). Затова броят на цифрите му ще е (3-2)+1=2. Тогава частното ще е двуцифрено число.

Лесно откриваме, че 41 се обира само веднъжм в 65. Като извадим 41 от 65 получаваме 24. Сваляме последната цифра от делимото и остава да видим колко пъти 41 се побира в 246.

Лесно проверяваме, че 10.41 е 410. Далеч сме от 246, затова е добре да пробваме с доста по-малко число. Например 5! Пресмятаме 41.5=205. Получаваме, че разликата на 246 и 205 е точно 41! Прибавяме още една единица към 5 и получаваме:

656:41=16

Проверка:

16.41=656

Време е за един последен пример. След което можеш да се упражниш с теста в края на статията!

Да пресметнем: 948:237

Първо определяме от колко цифри ще е частното. Делимото и делителят са с равен брой цифри, затова частното ще е едноцифрено число.

Виждаме, че 10.237 е 2370, което е много по-голямо то 948. Добре е да опитаме с някое по-малко число- 5 или 6.

Опитваме с 6 и получаваме 6.237=1422. Получихме по-голяма стойност, при това няма да е достатъчно да намалим само с една единица, тъй като от 1422 до 948 разликата е повече от 237. Получаваме:

4.237=948

Тогава : 948:237=4.

Опитай да приложиш триковете при примерите в теста!