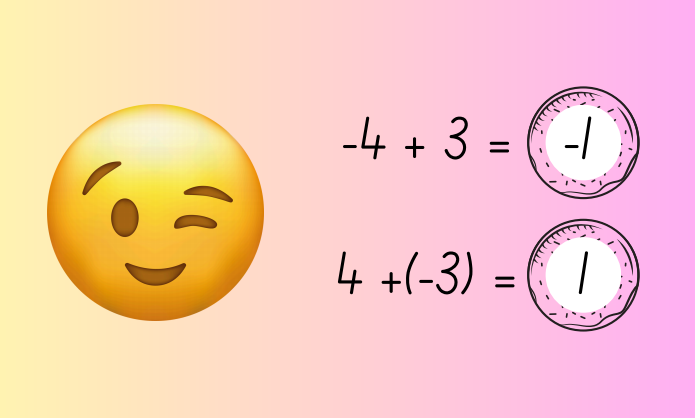Събиране на рационални числа с различни знаци
Здравейте, шестокласници! Вече се научихме да събираме рационални числа с еднакви знаци, например две отрицателни числа, но да видим как ще събираме положително и отрицателно число. Време е за ново правило!

Много е важно да внимаваме дали събираме числа с различни или с еднакви знаци. Можеш да си припомниш правилата за събиране на рационални числа с еднакви знаци ето тук:
Събиране на рационални числа с различни знаци
Да видим как ще събираме отрицателно и положително число. Да си представим, че изкачваме стълбище. Условно едно от стъпалата е прието за числото 0. Стъпалата преди него имат отрицателна стойност и са подредени като на числова ос. Стъпалата над него са с положителни стойности. Да видим как се придвижва нашият приятел.

В началото е застанал на стъпaлото, означено с —3. След това се е изкачил с 8 стъпала и е стигнал до стъпало, означено с числото 5. Можем да запишем следното равенство:
—3+8 = +5
Да разгледаме двете събираеми и помислим кои са техните модули.
I—3I=3, I8I=8
Веднага ще се сетим, че ако извадим модулите им, ще получим числото 5. Тогава да поразсъждаваме за знакът на сборът на двете числа- той е същият като на числото с по-големия модул!
Ако си забравил как се намира модул на рационално число, можеш да си припомниш тук:
Абсолютна стойност (модул) на рационални числа.

Тогава две рационални числа с различни знаци ще събираме така:
- От по-големия модул изваждаме по-малкия
- Пред сбора записваме знака на числото с по-големия модул
Тогава да видим какво ще получим, ако разменим знаците на събираемите от нашият пример.
3+( —8) = —5
Разликата на модулите е 5, но отрицателното събираемо с по-големия модул, затова сборът ще е отрицателното число —5.
Лесни примери със събиране на положително и отрицателно число
Да упражним нашето правило като пресметнем този израз:
—24 2/5 + 3,75
Нека първо да определим знакът на сбора, за да не забравим накрая да го поставим. Числото с по-големия модул е —24 2/5, затова сборът ще е отрицателно число. Остава да извадим от по-голямата абсолютна стойност по-малката. Така получaваме:
-24 2/5+3,75 = —(24 2/5—3,75) = — (24,4—3,75) = —20,65

Обърна ли внимание, че записахме обикновената дроб —24 2/5 като десетична дроб — 24,4 ? Можеш да решиш задачата и като запишеш десетичната дроб 3,75 като обикновена 3 3/4.
Да решим още една задача!
12,5+((—13,75)+2,85)
Тук скобите имат две значения- да отделят отрицателното число и да укажат реда на действие.
Нека първо извършим действието в скобите. Веднага се вижда, че отрицателното число има по-голям модул. Остава да извадим от по-голямата абсолютна стойност по-малката.
12,5+((—13,75)+2,85) = 12,5+(—(13,75—2,85))=12,5+(—10,9)
След като сме готови със стойността в скобите, можем да пресметнем последния сбор:
12,5+(—10,9) = + (12,5 — 10,9) = + 1,6
Този израз можем да запишем и много по-кратко, когато сме наясно с правилата за събиране и изваждане на рационални числа. Ето как:
12,5+((—13,75)+2,85) =12,5+(—10,9) = + 1,6
Сбор на противоположни числа
Да видим какво ще получим, когато съберем две противоположни числа. Например: —12,5+12,5
Модулите на двете числа са напълно равни, затова тяхната разлика ще е равна на 12,5—12,5 = 0.
Можем да обобщим правилото за всички противоположни числа:

Сборът на противоположните числа е равен на 0!
Когато в израза имаме събираеми, които са противоположни числа, можем да ги унищожим, тъй като сборът им е нула и да ги задраскваме по този начин:
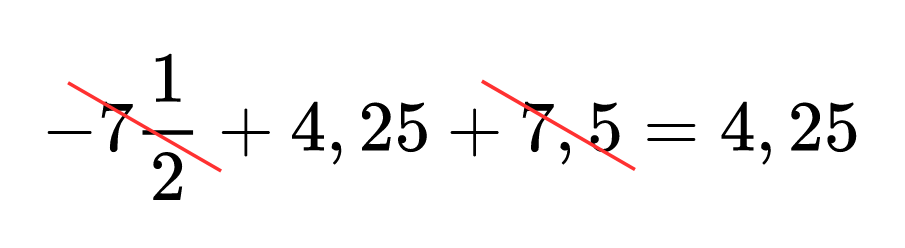
По-сложни изрази със сбор на рационални числа

Вече знаем правилата за събиране на рационални числа с еднакви и различи знаци и можем да ги използваме в по-сложни изрази! Освен това можем да използваме различни подходи при решаване на една и съща задача!
Да разгледаме ето този израз:
—56,5+39,4+(—27,4)+32,8+6,5+ (—9,4)
—56,5+39,4+(—27,4)+32,8+6,5+ (—9,4) = — (56,5+27,4+9,4)+(39,4+32,8+6,5) = —93,3+78,7 = —14,6
—56,5+39,4+(—27,4)+32,8+6,5+ (—9,4)= (—56,5+6,5)+(39,4+(—9,4)+(32,8+(—27,4)) = —50+30+5,4 =
= —20+5,4 = —14,6
—56,5+39,4+(—27,4)+32,8+6,5+ (—9,4)= (—56,5+39,4)+(—27,4)+32,8+6,5+ (—9,4) =
=(—17,1+(—27,4))+32,8+6,5+ (—9,4) = (—44,5+32,8)+6,5+ (—9,4)= (— 11,7+6,5)+(—9,4) = —5,2+(—9,4)=
= —14,6

Когато в израза имаш повече от две събираеми, помисли дали не можеш да ги комбинираш, така че да смяташ рационално! Ако не намериш такъв вариант, тогава е добре да събереш поотделно отрицателните и положителните числа.
Реши теста, за да се упражниш добре!