Здравейте, ученици! Днес ще се запознаем с важни умения в работата с дроби: събиране и изваждане на обикновени дроби с еднакви и различни знаменатели. Ще разгледаме как да се справяме с дроби, които имат еднакви знаменатели, и какво да правим, когато знаменателите са различни. Ще ви представим изчислителни примери, както и практически задачи.

1. Теоретична част

1.1. Обикновени дроби с еднакви знаменатели

1.1.1. Събиране на обикновени дроби с еднакви знаменатели

Когато дробите имат еднакви знаменатели, тяхното събиране е много лесно. Трябва просто да съберем числителите, докато знаменателят остава същия.

Пример:

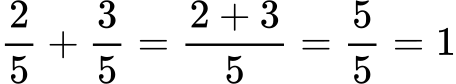
От записаното по-горе можем да направим следните изводи за събирането на об. дроби с равни знаменатели:

1. Събират се само числителите:

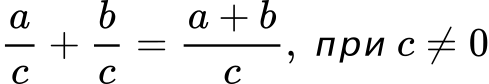
2. Знаменателят се запазва същия (виж горния пример).

1.1.2. Изваждане на обикновени дроби с еднакви знаменатели

При дроби, които имат еднакви знаменатели, тяхното изваждане също е много лесно. Просто изваждаме числителите, докато знаменателят остава същия.

Пример:

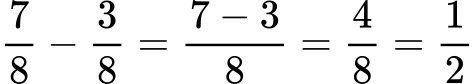
От записаното по-горе можем да направим следните изводи за изваждането на об. дроби с равни знаменатели:

1. Изваждат се само числителите:

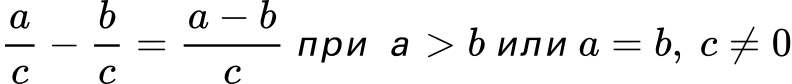
2. Знаменателят се запазва същия (виж горния пример).

3. Хубаво е да направим проверка на изваждането!

1.2. Обикновени дроби с различни знаменатели

1.2.1. Събиране на обикновени дроби с различни знаменатели

Когато знаменателите са различни, трябва първо да намерим общ знаменател, преди да съберем дробите. Общият знаменател е най-малкото общо кратно (НОК) на знаменателите. След като приведем дробите под общ знаменател, събираме числителите.

Пример:

1. Намираме НОК на 4 и 6, което е 12.
2. Преобразуваме дробите: 1/4 = 3/12; 1/6 = 2/12
3. ​Събираме: 3+2/12 = 5/12

От записаното по-горе можем да направим следните изводи за събирането на об. дроби с различни знаменатели:

1. Дробите се привежат към общ знаменател (НОЗ):

2. Събираме получените дроби с равни знаменатели:

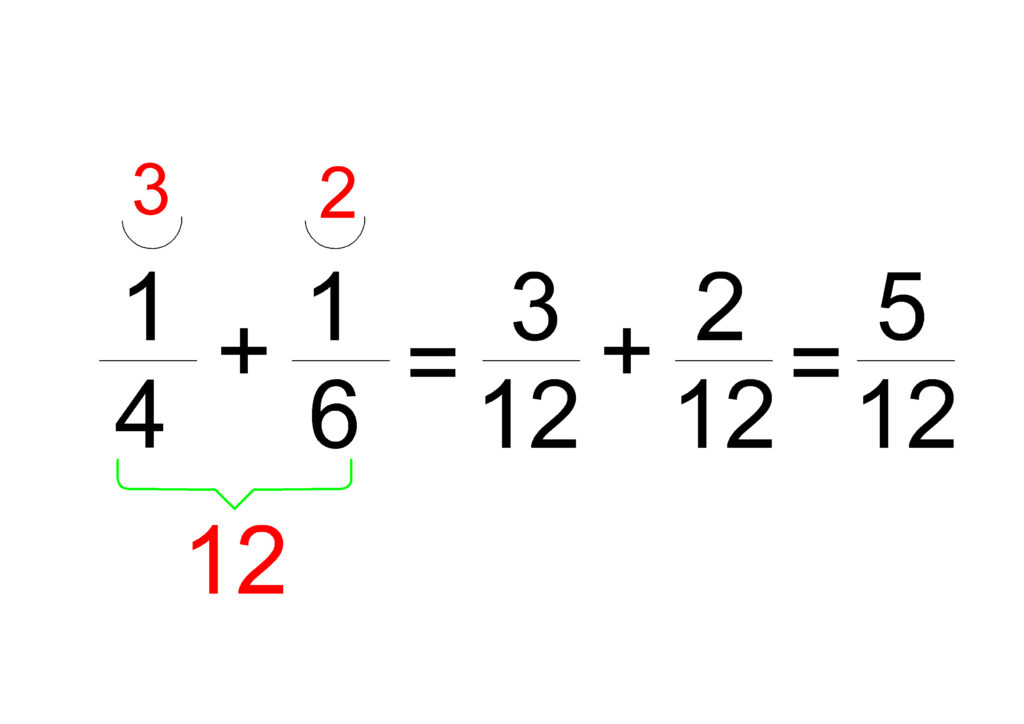
1.2.2. Изваждане на обикновени дроби с различни знаменатели

Както и при събирането, когато знаменателите са различни, трябва първо да намерим общ знаменател, преди да извадим дробите. Общият знаменател е най-малкото общо кратно (НОК) на знаменателите. След като приведем дробите под общ знаменател, изваждаме числителите.

Пример:

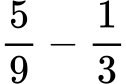
1. Намираме НОК на 9 и 3, което е 9.
2. Преобразуваме дробите: 5/9 остава същата, а 1/3 става 3/9
3. Извършваме изваждането: 5-3/9 = 2/9

Стигаме до следните изводи за изваждането на об. дроби с различни знаменатели:

1. Дробите се привежат към общ знаменател (НОЗ):

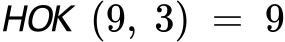
2. Изваждаме получените дроби с равни знаменатели:

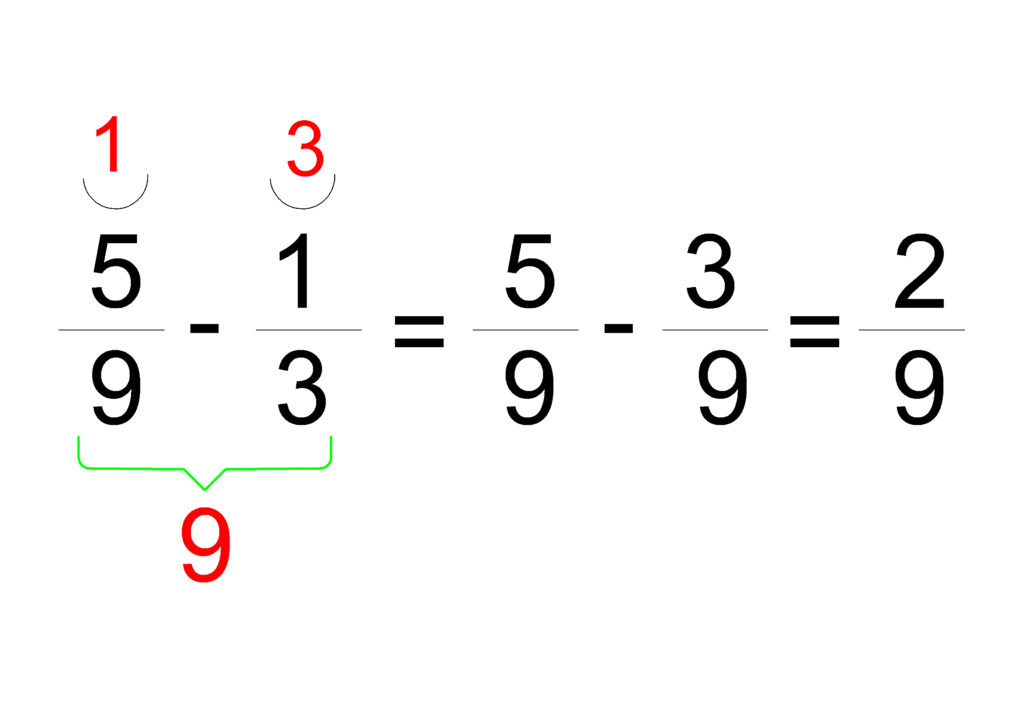
3. Хубаво е да направим проверка на изваждането!

2. Примерни задачи за изчисление

1. Извършете събирането:

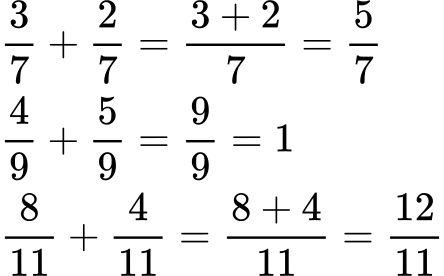
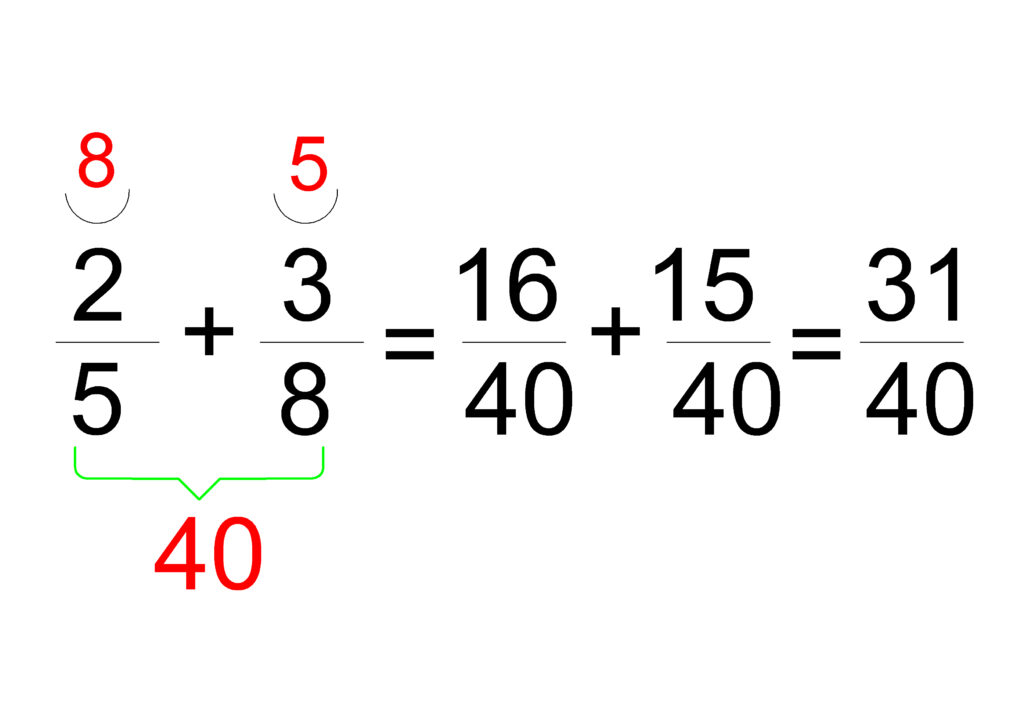
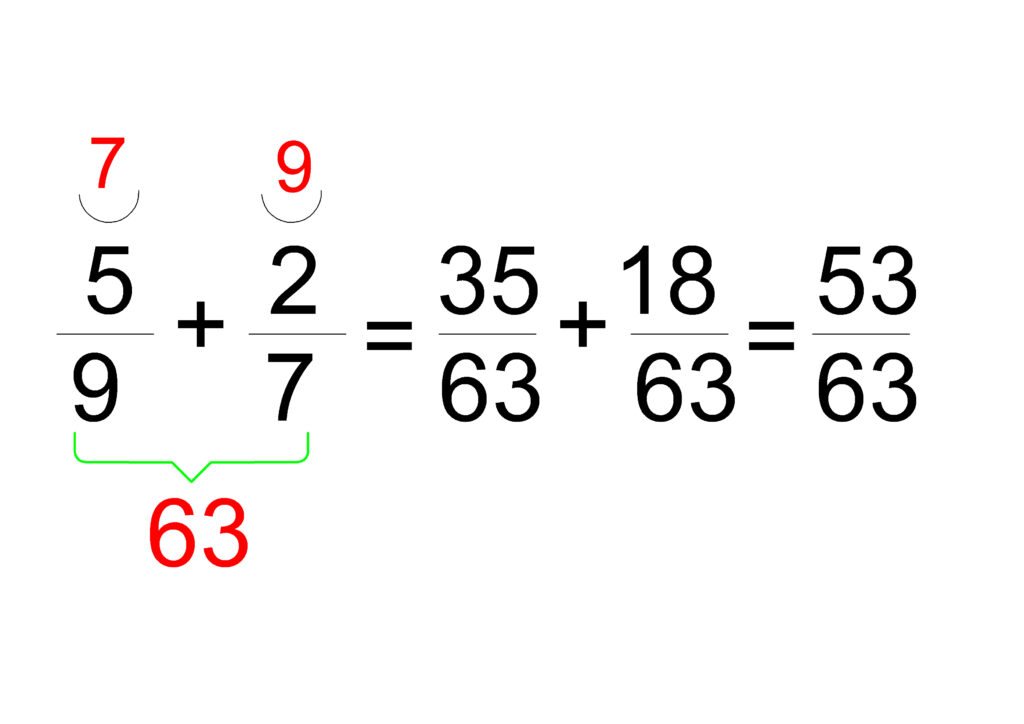
2. Извършете изваждането:

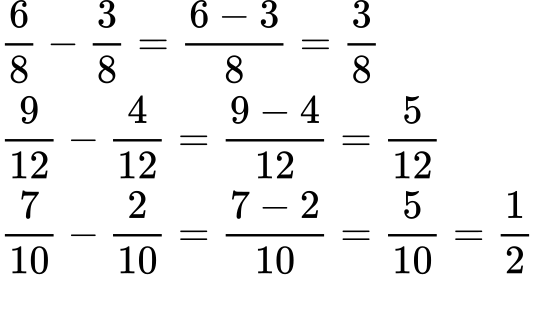
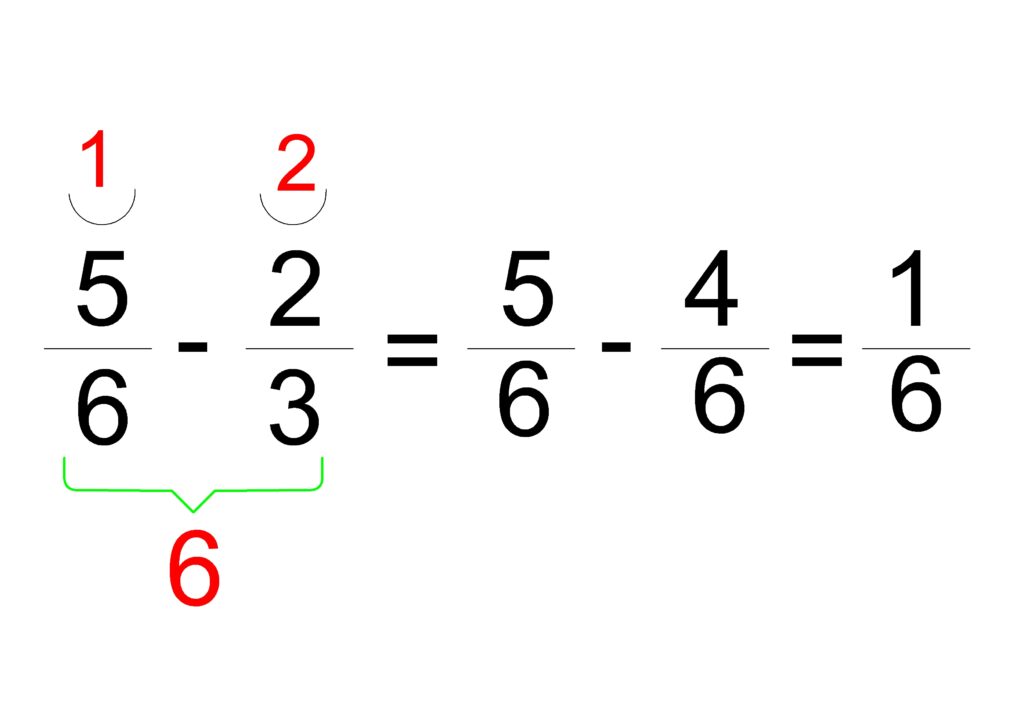
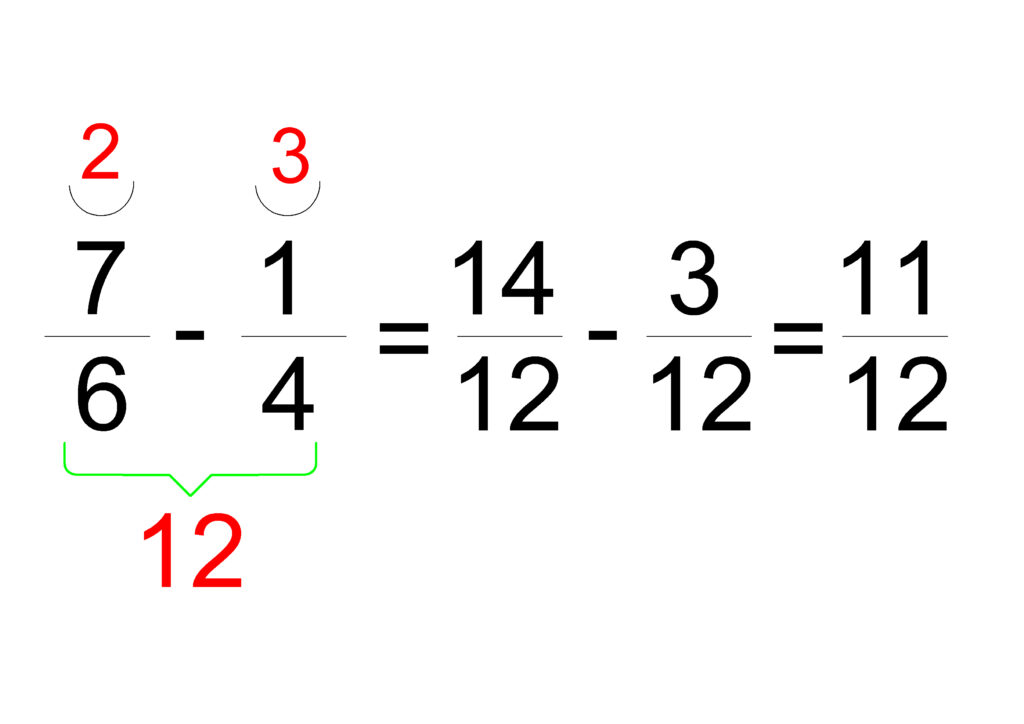
3. Текстови задачи

1. Мариана засадила през почивните дни 3/5 от цветята, които имала да посади, и още 2/15 от тях- през седмицата.

а/ Каква част от цветята е засадила Мариана?

б/ Каква част от цветята й е останала да засади?

Първо правим съкратен запис на задачата, така:

1. На концерт присъствали мъже, жени и деца. 2/5 от зрителите били деца, а 1/2​ мъже. Каква част от всички зрители били жените?

И тук правим съкратен запис на задачата, така:

4. Практически задачи

1. Строителна фирма изградила язовирна стена. 1/4 от тази стена се намирала в почвата, а 2/5 от нея във водата. Изчислете каква част от стената се виждала над водата.

Отново правим съкратен запис на задачата, така:

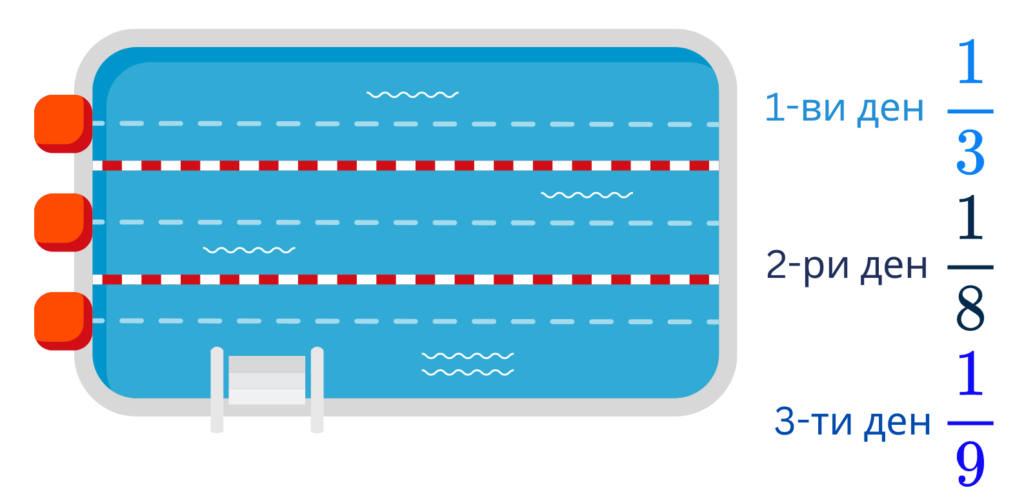
2. Олимпийски басейн трябвало да бъде изпразнен, с цел почистване, за три последователни дни. Първият ден изпразнили съответно 1/3 от него, вторият 1/8, а последния ден – 1/9 от него.

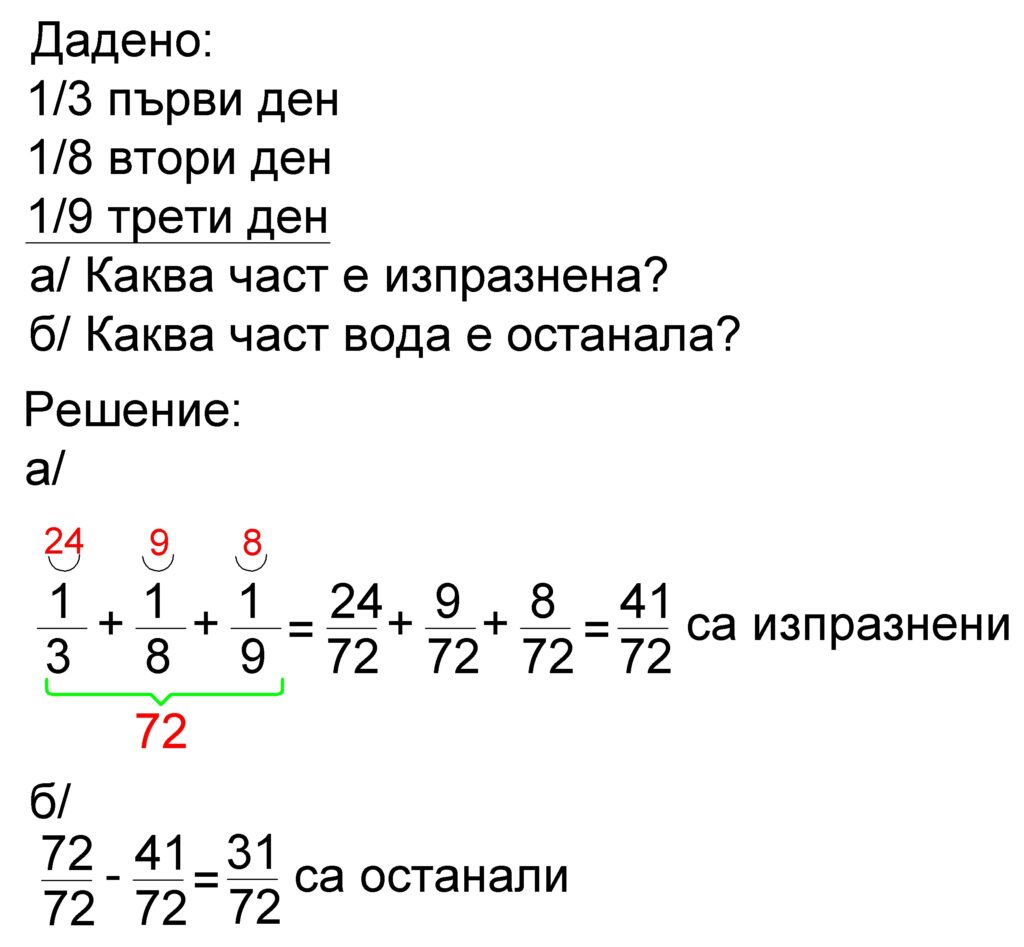
а/Определете каква част от него е изпразнена първите три дни.

б/ Каква част от водата в басейна е останала?

Правим съкратен запис на задачата:

5. Заключение

Събирането и изваждането на дроби е важно умение, което ще използвате не само в математиката, но и в ежедневието. Запомнете, че когато знаменателите са различни, винаги трябва да намирате общ знаменател, преди да събирате или изваждате числителите. С практика тези умения ще станат по-лесни и ще ги използвате с увереност. Ако имате някакви колебания и не сте сигурни дали сте разбрали всичко, можете да изгледате видеото долу, в което Математко отново обяснява основните правила на урока. Ако пък смятате, че всичко ви е ясно, опитайте да решите теста към урока.

До нови математични приключения!