Събиране и изваждане на многочлени
Здравей, приятелю!
Представи си, че многочлените са като кутии с играчки. В една кутия има кубчета, в друга – топки, в трета – пъзели. Ако искаме да съберем кутиите, трябва да преброим еднаквите играчки заедно, а не да смесваме всичко хаотично.
Точно така работи и събирането и изваждането на многочлени – групираме подобните членове и ги събираме (или изваждаме) правилно.
1. Теоретична част
1.1. Какво означава да събираме или изваждаме многочлени?

Събираме или изваждаме многочлени по правилата за събиране и изваждане на едночлени. Прилагаме правилата за разкриване на скоби тогава, когато те присъстват в примера.

- За да съберем или извадим два многочлена, групираме подобните едночлени и събираме (или изваждаме) техните коефициенти.
- Подобни са тези едночлени, които имат еднакви променливи, повдигнати на същите степени.
1.2. ✅ Пример 1: Събиране на многочлени

Решение:
Групираме подобните членове:
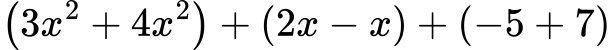
Пресмятаме:
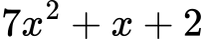
➡ Резултат: 7x2 + x + 2
1.3. ✅ Пример 2: Изваждане на многочлени
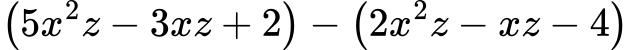
Решение:
Разкриваме скобите (внимавай с минуса!):
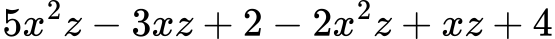
Групираме подобните:
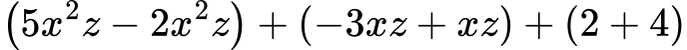
➡ Резултат: 3x2z − 2xz +6
1.4. ✅ Пример 3: Събиране с повече членове
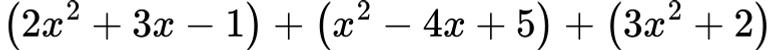
Решение:
Събираме подобните:
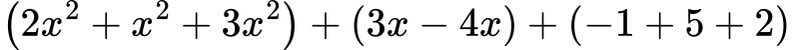
➡ Резултат: 6x2 − x + 6
2. Основни стъпки, които да запомниш:

- Премахни скобите, като внимаваш за знаците.
- Групирай подобните членове.
- Събери или извади коефициентите.
- Запиши крайния резултат в нормален вид.
3. Упражнителни задачи: ✍️
Задача 1:
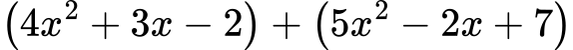
Решение:

Задача 2:

Решение:
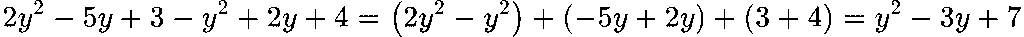
Задача 3:

Решение:
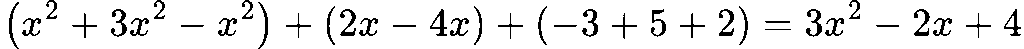
4. Заключение
Събирането и изваждането на многочлени е като пъзел – търсиш подобните парченца и ги подреждаш заедно. Ако запомниш правилото за групиране на подобните членове, задачите ще станат лесни и дори забавни. След още няколко упражнения ще събираш и изваждаш многочлени като истински математик! 🔢💪