Степенуване. Умножение и деление на степени с равни основи.
Здравейте, ученици! След като вече се запознахме с действието степенуване, е време да се научим на някои много интересни правила! Днес ще разберем как лесно и бързо да извършваме умножение и деление на степени с равни основи.

Ако имаш нужда да си припомниш какво представлява степенуването на рационалните числа, то прочети тази статия: Степенуване с естествен степенен показател
Умножение на степени с равни основи
Да разшифроваме сега това тайнствено заглавие – хем умножение, хем степени с равни основи!
Първо да разгледаме примери за степени с равни основи:
34, 37, 311 — тук всички степени имат една и съща основа, числото 3.
(1/2)10, (0,5)4 — тези две степени също са с равни основи, тъй като 1/2 = 0,5
След като вече разбрахме кои степени са с равни основи, да видим как изглежда произведението на степени с равни основи:
34. 33. 32
А сега да представим всяка степен като произведение:
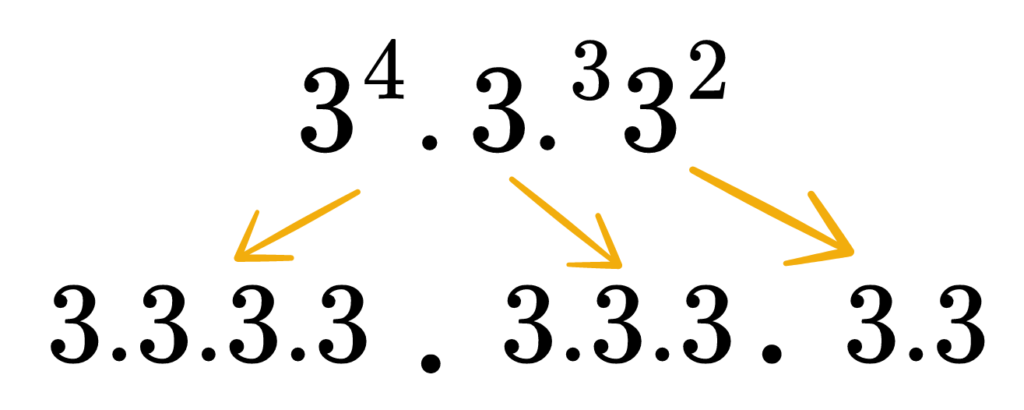
Ако преброим множителите, ще видим, че те са точно 9. Затова можем да запишем произведението ето така:
34. 33. 32 = 34+3+2 = 39

Можем да запишем произведението на степени с равни основи като степен със същата основа и степенен показател, който е равен на сбора от степенните показатели на множителите.
В математиката правилата се обобщават много лесно с буквен запис!
am.an = am+n
Нека да запишем следващото произведение като степен с основа 2:
24.8.32.2.27
В това произведение се виждат веднага три степени с основа числото 2. Не забравяйте, че всяко рационално число можем да запишем като степен със същата основа и степенен показател 1!
Щом се иска от нас да представим произведението като степен, то трябва да помислим как да запишем числата 8 и 32 като степени на числото 2. Ами всъщност е много лесно:
8 = 2.2.2 = 23
32= 2.2.2.2.2 = 25
Тогава представяме нашето произведение като степени с равни основи и после прилагаме правилото, което записахме по-горе:
24.8.32.2.27 = 24.23.25.21.27 = 24+3+5+1+7 = 220
Деление на степени с равни основи
Със сигурност се досещате вече какво ще е правилото за деление на степени с равни основи, но нека да видим как достигаме до него!
Да запишем частното (—0,2)5: (—0,2)2 като степен с основа —0,2 и да заменим знака за деление с дробна черта.
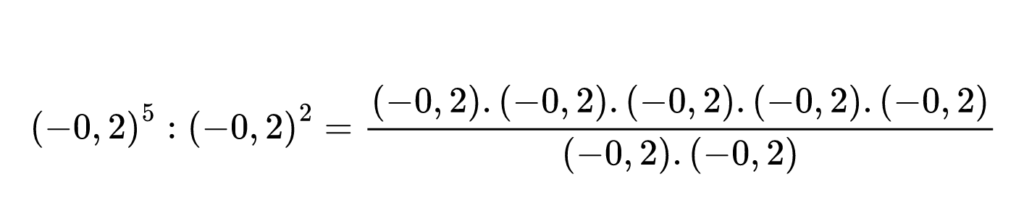
Хайде сега да съкратим множители от числителя и знаменателя:
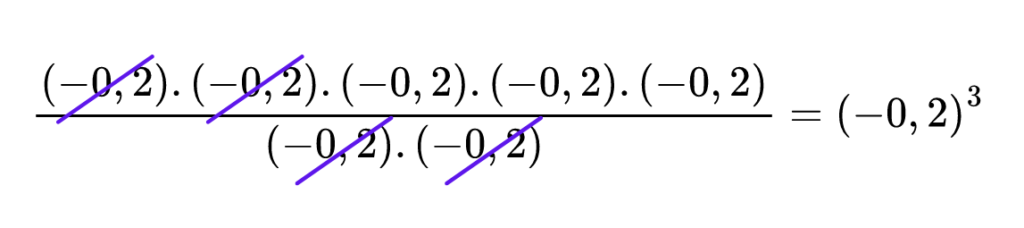

Досети ли се вече за правилото за деление на степени с равни основи?
Можем да запишем частното на степени с равни основи като степен със същата основа и степенен показател, който е равен на разликата на степенните показатели на делимото и делителя.
am:an = am—n
Да запишем като степен с основа 7 следващия пример:
(717:712):73
Първо извършваме действието в скобите и след това прилагаме отново правилото за деление на степени с равни основи.
(717:712):73 = 717-12:73 = 75:73= 75-3 = 72
Искам да ви предизвикам с един малко по-различен пример! Ето го и него:
52:55
Да използваме нашето правило за деление на степени с равни основи:
52:55 = 52—5 = 5—3
Да запишем сега същия пример, като заменим делението с дробна черта:
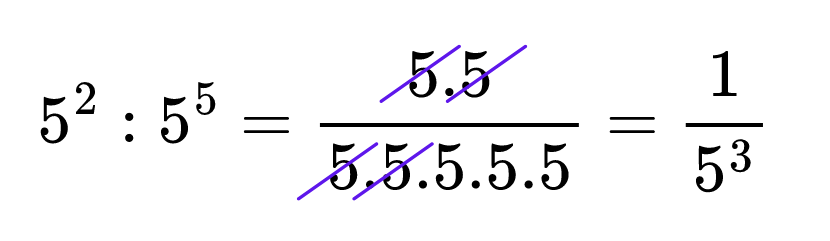
Видяхте ли как можем да запишем степента с отрицателен степенен показател?
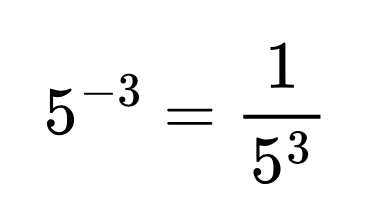
Степен с отрицателна основа и степен с нулева основа
От предишната задача можем да изведем правилото за степен с отрицателна основа. Ако запишем реципрочното число на 5, а степенния показател стане положително число, ще получим нашия отговор:
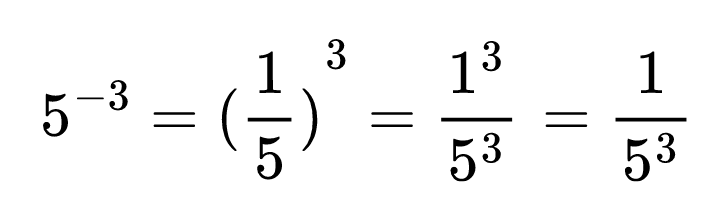
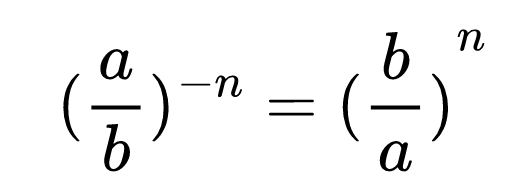
Степен с отрицателен степенен показател е равна на степен, която има реципрочна основа и положителен степенен показател.
Да пресметнем стойността на израза:
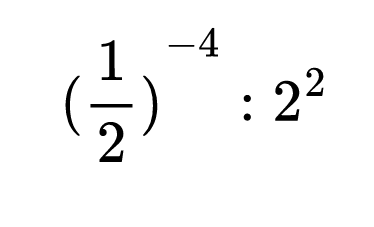
Записваме първо степента с отрицателен степенен показател като степен с положителен степенен показател и след това прилагаме правилото за деление на степени с равни основи.

А сега да видим какво ще получим, ако делим две степени с равни основи и равни степенни показатели:
124:124 = 124—4=120
Същия пример можем да запишем и така:
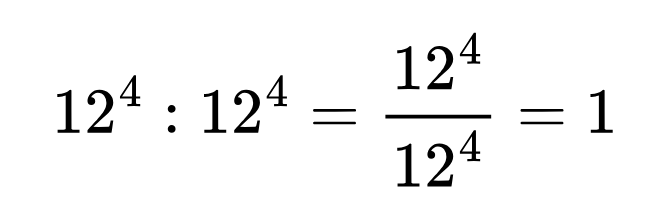
Ами тогава 120=1!
Да обобщим:

Степен, със степенен показател 0 и основа, различна от 0, е равна на 1!
а0 = 1, ако основата е различна от 0.
Да намерим стойността на следващия израз:
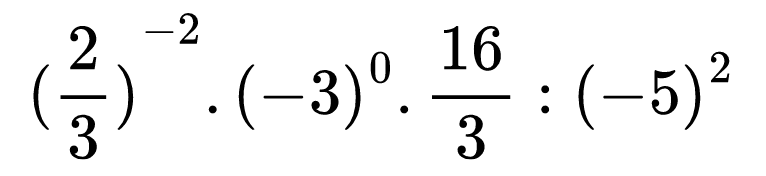
Да запишем първата степен с положителен степенен показател, останалите две степени можем да заменим с техните стойности:
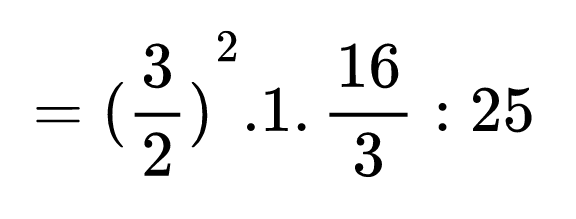
Готови сме да довършим израза, като запишем стойността на степента и съкратим, някои множители:
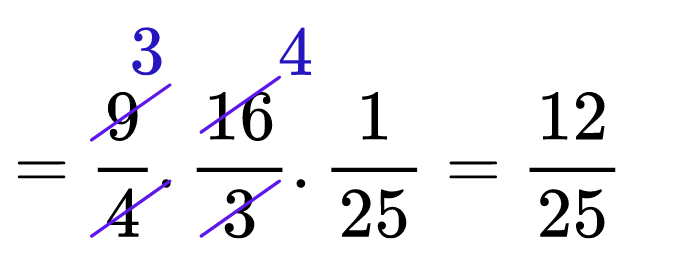
Време за упражнение! Може да решите следващия тест, за да упражните правилата!