Степенуване на произведение, частно и степен
Здравейте, шестокласници! Време е задачите със степенуване да станат още по-интересни! Днес ще научим правилата за степенуване на частно и произведение, както и за степенуване на степен.

Ако все още ти е трудно да разбереш степенуването и правилата, свързани с него, можеш да си припомниш статиите:
Степенуване на произведение
Да видим как можем да представим по различен начин 23.33
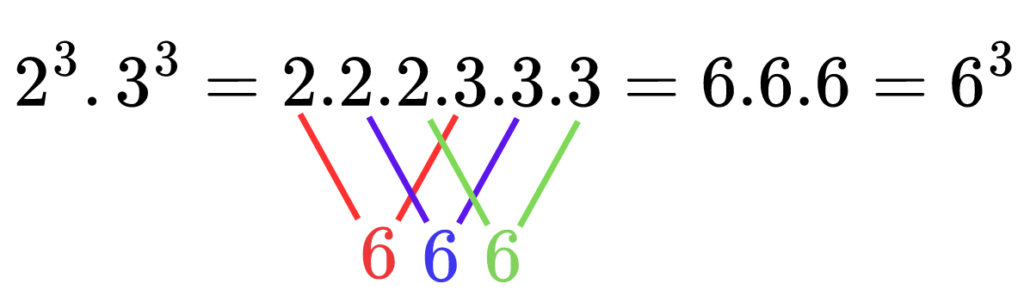

Когато имаме произведение на степени, които имат равни степенни показатели, можем да ги запишем като степен с основа, равна на произведението на двете основи и същия степенен показател.
Да обобщим правилото с букви:
an.bn=(a.b)n
Хайде да пресметнем стойността на следващия израз:
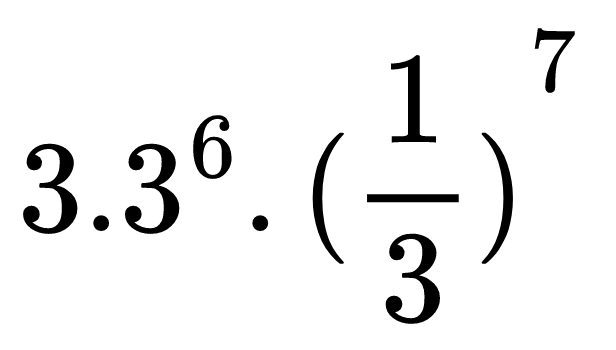
Тук не трябва да бързаме да пресмятаме всяка степен поотделно, а първо да помислим дали не можем да опростим малко израза.
Можем да използваме правилото за умножение на степени с равни основи и ще получим, че 3.36=37. След това веднага се забелязва, че получаваме произведение на степени с равни степенни показатели и за него ще приложим правилото за степенуване на произведение. Да видим какво ще се получи:
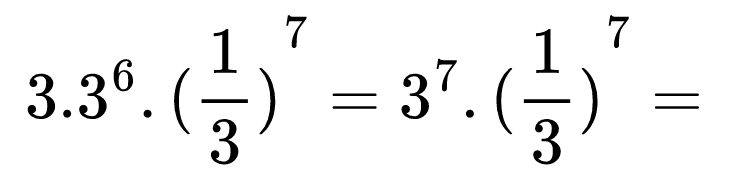

Степенуване на частно
За да стигнем до правилото за степенуване на частно, ще използваме, че знакът за деление можем да заменим с дробна черта.


Можем да запишем частното на степени, които имат равни степенни показатели, като степен с основа, равна на частното на двете основи и същия степенен показател.

Хайде да упражним правилото със следващия пример и да намерим стойността на израза:
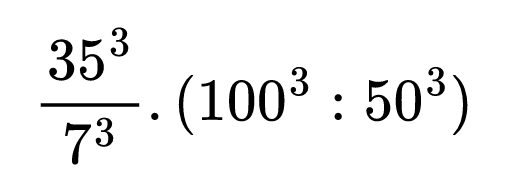
Прилагаме правилото за степенуване на частно, както в началото на израза, така и в скобите:
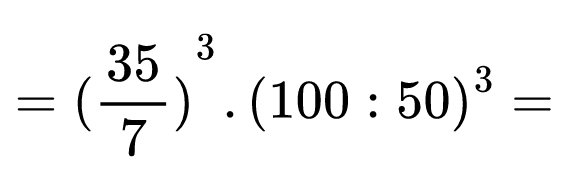
Остава да пресметнем частното на 35 и 7, както и това на 100 и 50. Довършваме изчисленията като прилагаме правилото за степенуване на произведение.
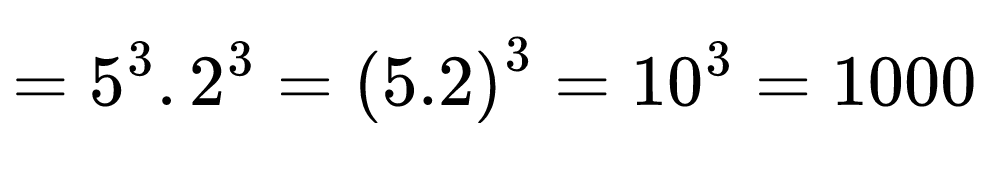
Степенуване на степен
Звучи много интересно как така ще степенуваме степен! Ами хайде да видим как можем да представим (102)3
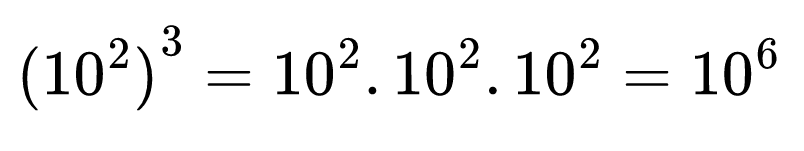
Първо записахме степента в скобите като произведение от три еднакви множителя, а след това записахме полученото произведение като степен.
Забеляза ли, че като умножим двата степенни показателя в началото, получаваме степенния показател в края? Хайде да обобщим правилото!

Можем да степенуваме степен, като умножим степенните показатели и запишем същата основа.
(am)n = am.n
Хайде сега да упражним новото правило, като запишем като степен следващия пример:
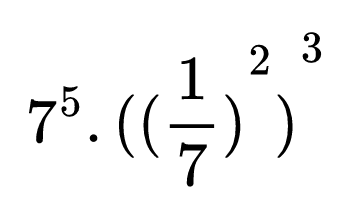
Първо прилагаме степенуването на степен с основа обикновената дроб 1/7.
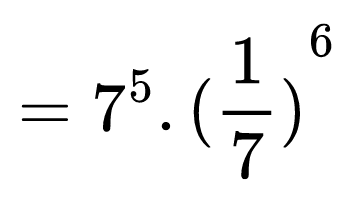
След това не бива да пресмятаме на колко са равни двете степени, а да поразсъждаваме как можем да използваме правилата дотук.
Най-удобно е да се сетим, че можем да представим (1/7)6 като произведение:

Приложихме правилото за степенуване на произведение и вече се получи много удобен израз. Сещаме се, че произведението на двете реципрочни числа в скобите е равно на 1 и довършваме задачата:
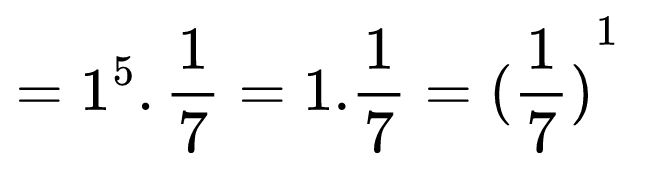
Накрая записахме отговорът като степен, тъй като това се искаше в нашето условие.
По-сложни примери със степенуване
Вече изучихме всички основни правила, свързани със степенуването на рационални числа. Сега е време да разгледаме една наистина майсторска задача:
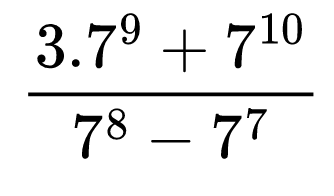
Веднага ви се иска да съкратите степените, но няма как да го направим все още, тъй като в числителя имаме сбор, а в знаменателя — разлика.
В такива примери първо трябва да разгледаме поотделно изразите в числителя и знаменателя.
В числителя по-ниската от двете степени е 79. Можем да представим 710 като 79.71
Сега разглеждаме израза в знаменателя. По-ниската степен е 77. Сега представяме 78 като 77.71

Вече се вижда, че можем да изнесем общ множител от израза в числителя и общ множител от израза в знаменателя. За числителя това е 79, а за знаменателя е 77.
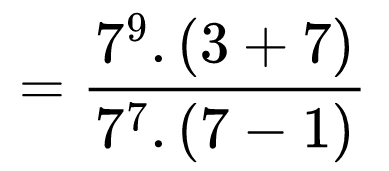
Сега можем да съкратим двете степени. В числителя ще получим 79-7 = 72 .

Пресмятаме степента 72 = 49 и съкращаваме числата 10 и 6 на 2. Ето и финалният резултат:
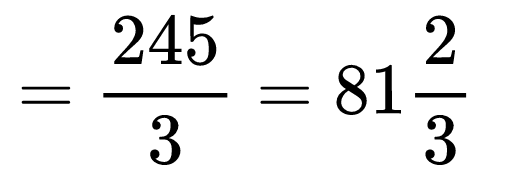

Време е да упражниш новите правила със следващия тест!