Днес ще разгледаме една много интересна и полезна тема в математиката – смесени числа. Ще се научите на преминаване от неправилна дроб към смесено число и обратно. Както и ще научите основните правила при събиране и изваждане на смесени числа. Това са важни умения, които ще ви помогнат не само в училище, но и в ежедневието.

В математиката понякога използваме специални числа, наречени смесени числа. Смесените числа ни помагат да представим лесно големи дроби, които са повече от едно цяло. В тази статия ще научите какво е смесено число, как се преминава от неправилна дроб към смесено число и как да събираме и изваждаме смесени числа.

1. Теоретична част

1.1. Какво е смесено число?

Смесено число е число, което съдържа както цяло число, така и дроб. Например, числото 2 3/4​ е смесено число, защото съдържа цяло число 2 и дробта 3/4​.

1.2. Какво е неправилна дроб?

Неправилна дроб е дроб, при която числителят (горното число) е по-голям или равен на знаменателя (долното число). Например, 7/4​ е неправилна дроб, защото числителят (7) е по-голям от знаменателя (4).

1.3. Как да преминем от неправилна дроб към смесено число?

За да преминем от неправилна дроб към смесено число, трябва да следваме следния ред от действия:

1. Да разделим числителя на знаменателя.
2. Полученото частно записваме като цяла част на смесеното число.
3. Остатъкът от делението става нов числител, а знаменателят остава същият (т.е. делителят е знаменател).

Пример: Да превърнем неправилната дроб 7/4 в смесено число:

• Делим 7÷4 =1 (цяло число) и остава 3 (остатък).
• Смесеното число е 1 3/4.

2. Събиране на смесени числа

Има няколко начина за събиране на смесени числа:

I начин.

1. Събираме целите части.
2. Събираме дробните части.
3. Получената цяла и дробна част се събират.

Пример: Да съберем 2 1/3+1 2/3:

1. Събираме целите части: 2+1=3
2. Събираме дробните части: 1/3+2/3=3/3=1
3. Добавяме резултатите: 3+1=4

II начин.

1. Преминаваме от смесено число към неправилна дроб.
2. Получените дроби се събират.
3. Ако резултатът е неправилна дроб, то я превръщаме в смесено число.

Пример: Да съберем отново 2 1/3+1 2/3:

Можем да запишем последователността от стъпки в този начин така:

3. Изваждане на смесени числа

Аналогично на събирането и тук са възможни няколко начина за изчисление:

I начин.

1. Изваждаме целите части.
2. Изваждаме дробните части.
3. Получената цяла и дробна част се събират.

Пример: Да извадим 3 1/4−1 2/4:

1. Изваждаме целите части: 3−1=2
2. Изваждаме дробните части: 1/4−2/4​. Тъй като 1/4​ е по-малка от 2/4​, заемаме 1 от цялата част. Представяме 3 като 2 4/4 и добавяме към дробната част тази, която е в нашата дроб, в случая това е 1/4. Така получаваме 2 5/4 и по този начин заместваме първото събираемо в нашия израз.
3. Сега вече можем да изваждим дробните части: 5/4−2/4=3/4
4. Изчисляваме целите части: 2−1=1 и получаваме 1 3/4

II начин.

1. Преминаваме от смесено число към неправилна дроб.
2. Получените дроби се изваждат.
3. Ако резултатът е неправилна дроб, то я превръщаме в смесено число.

Пример: Да разгледаме отново горния пример: 3 1/4−1 2/4

След изпълнение на стъпките се получава следното:

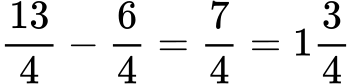
4. Задачи

4.1. Изчислителни задачи

1. Преобразувайте следните неправилни дроби в смесени числа:

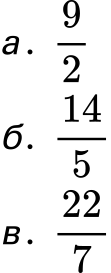
Рeшение:

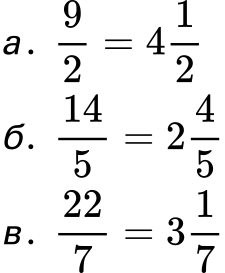
2. Съберете следните смесени числа:

Рeшение:

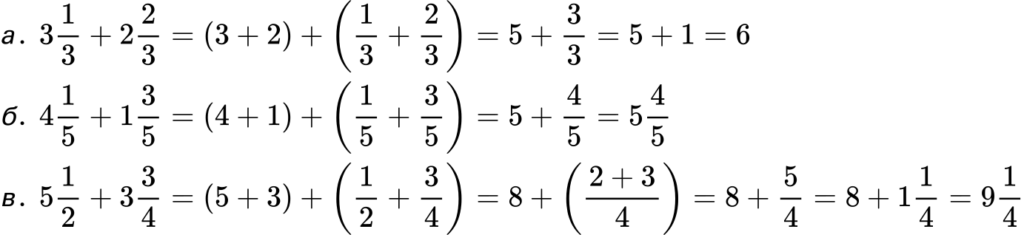
3. Извадете следните смесени числа:

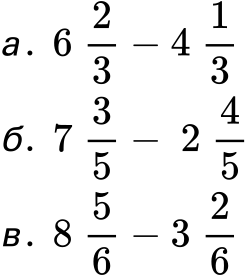
Рeшение:

4.2. Текстови задачи

1. Иван има 2 3/8 метра плат, а Мария има 1 5/8 метра плат. Колко метра плат имат общо двамата?

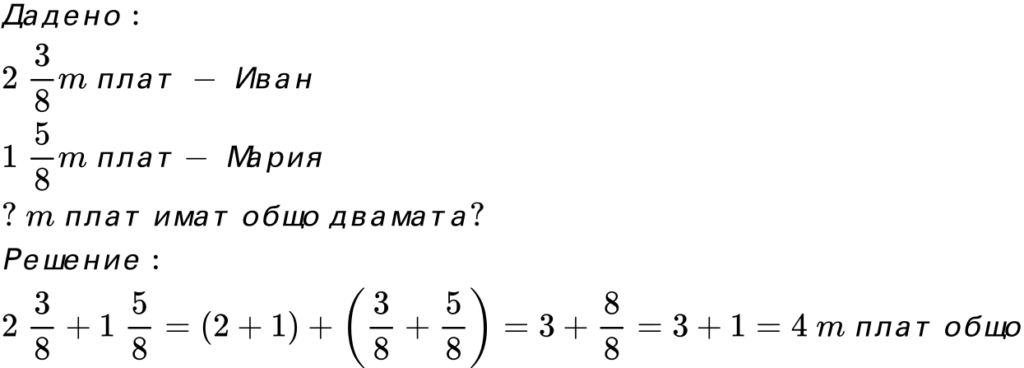
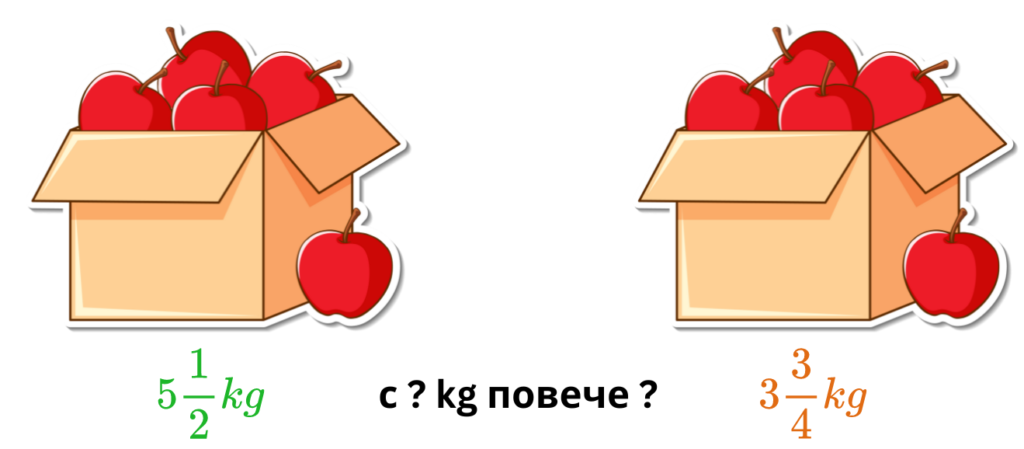
1. В една кутия има 5 1/2 килограма ябълки, а в друга кутия има 3 3/4 килограма ябълки. С колко килограма повече ябълки има в първата кутия?

4.3. Практически задачи

1. Ако един правоъгълник има дължина 7 2/3​ метра и широчина 4 1/3​ метра, каква е неговата обиколка?

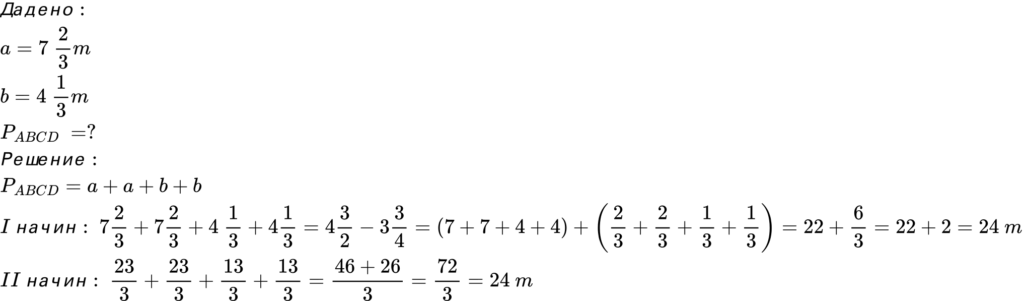
1. В един съд има 10 1/4​ литра вода. Ако се налеят още 3 2/4 литра, колко литра вода ще има общо?

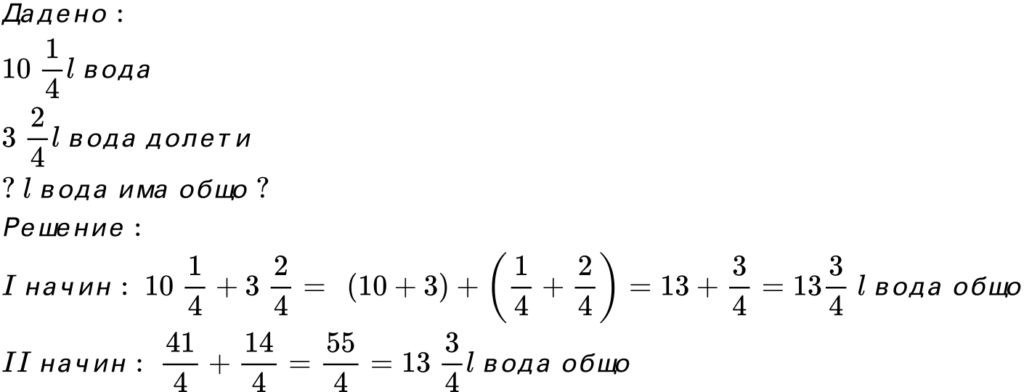
5. Заключение

Смесените числа са удобен начин за представяне на неправилни дроби. Умението да се преобразуват неправилните дроби в смесени числа и обратно, както и да се събират и изваждат смесени числа, е важно за решаването на много математически задачи. С тези знания ще можете лесно да се справяте с подобни изчисления.

Ако искаш да си припомниш правилата за събиране и изваждане на об. дроби, както изучените в този урок действия със смесени числа, изгледай следващото видео: