Рационални числа. Изобразяване на рационални числа върху числова ос.

Време е за нови предизвикателства! Вече познаваш обикновените и десетичните дроби и умееш да извършваш различни изчисления с тях. Сега идва ред да се срещнеш с важните рационални числа! След това ще се научим да ги изобразяваме върху числова ос.

Положителни и отрицателни числа

В живота си постоянно се сблъскваме с отрицателни числа.

• През зимата температурите навън са отрицателни (—15^o C)
• Намалението на стоките в магазина се показват с отрицателни числа (—20%)
• Понижаването на нивото на река се записва с отрицателно число (—14 cm)
• Точките от повърхността на Земята, които се намират под морското равнище, се записват също с отрицателни стойности (—120,5 m)

Положителните числа са тези, които са по-големи от нула. При записването им почти винаги се пропуска знакът “+” (плюс).

Отрицателните числа са по-малки от нула. При записването им винаги пред тях се поставя знак “—”(минус).

Рационални числа

Множеството от всички отрицателни, всички положителни числа и нулата, се нарича множество на рационалните числа. Не забравяй, че числото 0 не е нито положително, нито отрицателно!

Множеството на всички рационални числа се означава със специална буква- “Q”.

Тук попадат не само целите числа, но и дробните числа. Хайде да напишем всички цели рационални числа, между —5 и 7!

Тук попадат числата —4, —3, —2, —1, 0, 1, 2, 3, 4, 5 и 6.

Рационалните числа изобразяваме върху числова ос, а това ни помага да ги сравняваме подреждаме спрямо другите числа.

Числова ос

Числовият лъч вече е недостатъчен за нас, защото не можем да наместим на него отрицателните числа. Затова ни е нужна числова ос!

Нулата поставя началото на оста и я разделя на две посоки-положителна и отрицателна. Положителните числа изобразяваме надясно от 0, а отрицателните- вляво от 0.

Целите отрицателни числа се нанасят върху числовата ос по същия начин като целите положителни, но в отрицателната посока. Много често стрелката на отрицателната посока не се поставя.

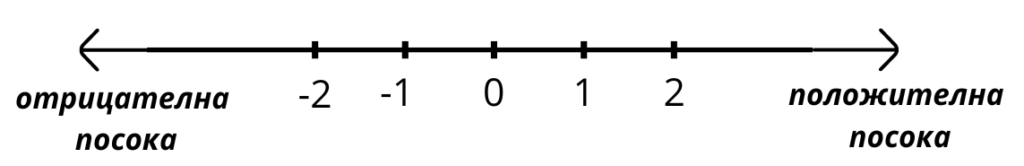
Всяко рационално число можем да изобразим с точка върху числовата ос.

Изобразяване на рационални числа върху числова ос

Положителните числа се изобразяват надясно от началото на числова ос (от числото 0).

Отрицателните числа се изобразяват наляво от числото 0.

Когато изобразяваме дробни числа върху числовата ос, трябва да помислим между кои две цели числа се намират!

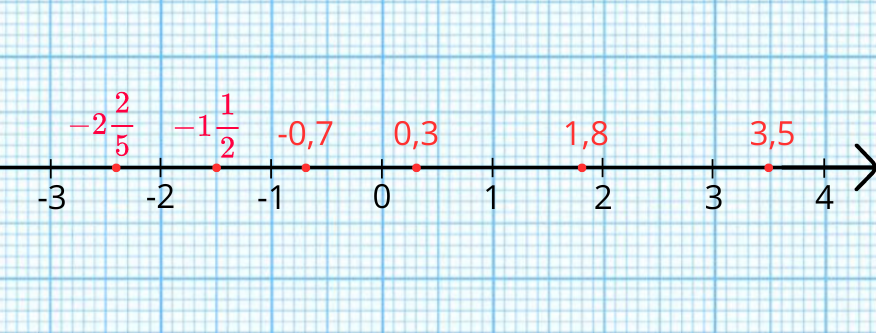
Нека да изобразим следните числа:

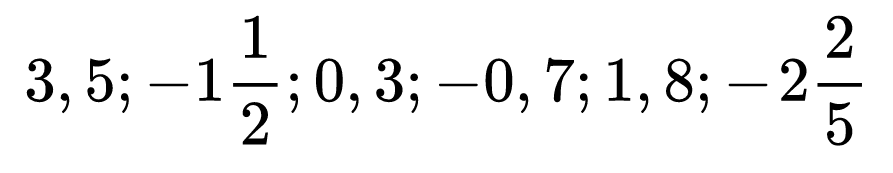
• Числото 3,5 се изобразява между 3 и 4.
• Числото -1 1/2 се изобразява между —1 и —2.
• Числото 0,3 се изобразява между 0 и 1.
• Числото -0,7 се изобразява между 0 и -1.
• Числото 1,8 се изобразява между 1 и 2.
• Числото -2 2/5 се изобразява между —2 и —3.

Ако използваме за единична отсечка 1 cm, то дробните числа ще се нанасят много лесно, като знаем, че 1 mm е една десета от сантиметъра.

Тогава 3,5 ще е точно на 5 mm от числото 3 т.е. по средата между 3 и 4.

—0,7 ще е на седмия милиметър от числото 0 в отрицателна посока.

1,8 е на осмия милиметър след числото 1 в положителна посока.

2/5=0,4, затова —2 2/5 ще е на четвъртия милиметър след числото —2 в отрицателна посока.

Сравняване на рационални числа

Всяко отрицателно число е по-малко от числото 0,

Всяка отрицателно число е по-малко от което и да е положително число.

От две отрицателни числа е по-голямо това, което се изобразява върху числовата ос по-близко до числото 0.

Тогава при сравняването на две рационални числа е важно да помислим за следното:

• Aко двете числа са с различни знаци, по-голямо е положителното число.
• От две отрицателни числа по-голямо е това, което се изобразява по-близко до нулата на числовата ос

Тогава да подредим по големина във възходящ ред следните числа:

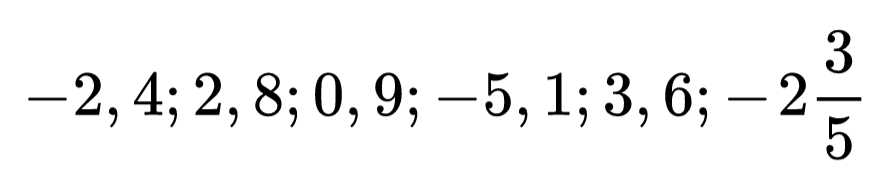
Положителните числа много лесно ще ги подредим по големина, тъй като тези знания ги имаме вече! Трябва да започнем от отрицателните числа, тъй като те са по-малки от положителните.

След това да видим отрицателните дробни числа между кои две цели числа се намират:

—2,4 е между —3 и —2.

—5,1 е между —6 и —5

—2 3/5=—2,6, намира се между —3 и —2.

Хайде да ги нанесем на оста, в началото е много по-лесно така, след това вече ще се сещаме веднага:

Най-близо до нулата се намира —2,4, след това е —2 3/5, а най-далеч е —5,1

Вече сме готови да подредим рационалните числа по големина във възходящ ред:

—5,1; —2 3/5, —2,4, 0,9; 2,8; 3,6

Време е за упражнение със следващия тест!