Здравейте, деца!

Днес ще научим нещо много интересно за дробите – какво е разширяване и съкращаване на обикновени дроби, както и правилата за извършване на тези математически действия. Готови ли сте? Хайде да започваме!

1. Какво са обикновените дроби?

Обикновените дроби са числа, които могат да бъдат представени по този начин:

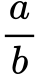
Например, 3/4 е обикновена дроб. Както вече знаем от урока за обикновени дроби числото, което се намира горе, в нашият случай това е 3, се нарича числител, а числото долу, т.е. 4, се нарича знаменател. А сега, нека видим какво означава да разширим дадена обикновена дроб!

2. Какво е разширяване на обикновена дроб?

Разширяването на дроб означава да умножим числителя и знаменателя с едно и също число. Така дробта изглежда по различен начин, но остава същата. Например, ако имаме дробта 2/5 и я умножим с 2, ще получим:

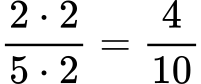
Виждаш ли?

2/5 и 4/10 са еднакви обикновени дроби!

Една дроб не се променя, ако числителят и знаменателят й се умножат с едно и също естествено число. Ако заменим дробта a/b с равна на нея: a.m/b.m, то ние казваме, че разширяваме тази дроб с допълнителния множител m. Записваме така:

Запомни! С нула не можем да разширим дадена обикновена дроб!

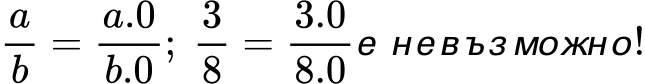
3. Какво е съкращаване на обикновена дроб?

Съкращаването на дроб означава да разделим числителя и знаменателя с едно и също число. Това също не променя стойността на дробта, но я прави по-проста. Например, ако имаме дробта 6/9 и я разделим с 3, ще получим:

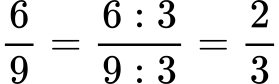
Така виждаме, че обикновените дроби 6/9 и 2/3 са еднакви!

От предходния пример можем да стигнем до извода, че ако разделим числителят и знаменателят на една дроб с едно и също естествено число, тази дроб няма да се промени. Това може да се запише така с букви:

3.1. Съкратими дроби:

Ако числителят a и знаменателят b, имат общ делител, който е различен от 1, то можем да кажем, че дробта е съкратима т.е.

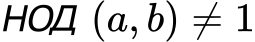
Например, дробта 12/18 е съкратима т.к. и числителят и знаменателят й могат да се разделят на едно и също естествено число 6:

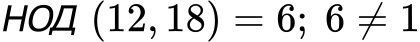
3.2. Несъкратими дроби:

Ако числителят a и знаменателят b, нямат общ делител, който е различен от 1 (т.е. a и b са взаимно прости числа), то можем да кажем, че дробта е несъкратима т.е.

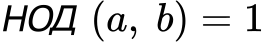
Например, дробта 5/7 е несъкратима т.к. нито числителят, нито знаменателят й имат общ делител:

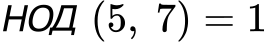
3.3. Как се извърша съкращаване на обикновена дроб?

Съкращаваме една дроб чрез последователно делене на числителя и знаменателя с техни общи делители:

Съкращаване може да се извърши и чрез делене на числителя и знаменателя с техния НОД т.е:

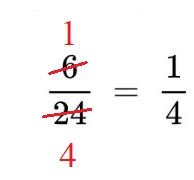
При разширяване или съкращаване на една обикновена дроб с едно и също естествено число тя НЕ СЕ ПРОМЕНЯ!

4. Примери за разширяване и съкращаване на дроби

Пример 1: Разширяване на дроб
Имаме дробта 3/4. Разширяваме я с 2:

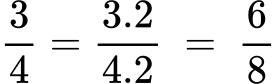
Пример 2: Съкращаване на дроб
Имаме дробта 8/12. Съкращаваме я с общия делител 2 или с НОД = 4:

5. Забавни задачи

Задача 1
Иван има 5/6 от шоколад. Той решава да раздели шоколада на по-малки парчета, като умножи числителя и знаменателя на дробта с 2. Колко парчета шоколад ще има той?

Решение:

Иван ще има 12 по-малки парчета шоколад.

Задача 2
Мария има 15/20 от пица. Тя иска да опрости дробта, за да види колко пълни части от пицата има. Намери опростената дроб.

Решение:
Най-големият общ делител на 15 и 20 е 5. Съкращаваме дробта с 5 и получаваме:

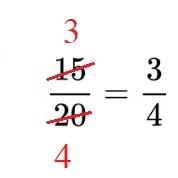
Мария има 3/4 от пицата.

Задача 3
Георги има 4/7 от една ябълка. Той решава да разшири дробта, като умножи числителя и знаменателя с 3. Колко части от ябълката ще има Георги?

Решение:

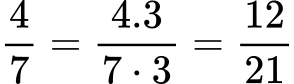
Георги ще има 12/21 от ябълката.

Задача 4
Анна има 12/18 от една торта. Тя иска да съкрати дробта, за да види колко пълни части от тортата има. Намери опростената дроб.

Решение:
Най-големият общ делител на 12 и 18 е 6. Съкращаваме дробта и получаваме:

Анна има 2/3 от тортата.

Задача 5

Неработните дни през месец май 2024 г. са 12. Работните дни от този месец са:

A/ 3/10;

Б/ 12/31;

В/ 19/31;

Г/ 7/10;

Решение: Тъй като в месец май 2024 г. е имало 31 дни, от които 12 са били неработни, то тези дни могат да се представят като обикновена дроб като: 12/31. Следователно, работните дни от този месец ще получим като извадим от общия брой дни т.е. 31 неработните дни т.е. 12. Оттук следва, че 19 са работните дни. Представени като дроб ще бъдат 19/31 т.е. верния отговор е подточка В).

Отлично! Вече знаеш как се разширяват и съкращават обикновените дроби, както и кои тях са съкратими и несъкратими. Ако искаш да изпробваш своите знания и умения, можеш да опиташ да решиш тестовете по долу!

Математико ти желае успех! До нови математични приключения!