Разлагане чрез комбинирано използване на различни методи
До този момент вече познавате няколко начина за разлагане на многочлени на множители:
- чрез изнасяне на общ множител;
- чрез формулите за съкратено умножение;
- чрез групиране.
Но в математиката често срещаме по-сложни изрази, които не могат да се разложат само с един метод. Тогава се налага да комбинираме различни техники – като истински „алгебрични детективи“. 🕵️♂️
Разлагане чрез комбинирано използване на различни методи ни позволява да разкрием структурата на израза стъпка по стъпка, докато стигнем до напълно разложен вид.
1. Теоретична част
1.1. Основни методи, които комбинираме:

- Изнасяне на общ множител – ако всички или някои членове имат такива.
- Формули за съкратено умножение – ако изразът наподобява квадрат на сбор, квадрат на разлика или разлика на квадрати.
- Групиране – ако никой от горните методи не работи директно, но можем да подредим членовете по групи.
1.2. Как да изберем метода, който да приложим в задачата?

- Първо проверяваме дали има общ множител: ако има такъв, то го изнасяме пред скоби.
- Ако няма → търсим формули за съкратено умножение: ако има формула (в явен или неявен вид) я прилагаме и я използваме при разлагането.
- Броим членовете на многочлена. Ако са четен брой: разлагаме чрез групиране, ако е възможно; ако са нечетен брой: се стремим да ги направим повече на брой, за да можем да ги групираме.
- Ако и това не може да се приложи → пробваме с групиране.
- Често е нужно първо да изнесем израз или променлива пред скоби, за да остане израз, подходящ за формула или групиране.
1.3. Квадратен тричлен
Тричлени от вида: ax2 + bx + c (c≠0) са от втора степен и се начират квадратни тричлени.
1.4. Допълване до точен квадрат
За да определим дали един квадратен тричлен е разложим или е неразложим, можем да използваме метод, наречен “допълване до точен квадрат”.
Например в израза:
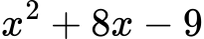
Допълваме така:
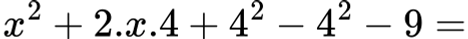
Отделяме точен квадрат:
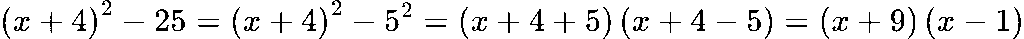
2. Примери с решения✅:
Пример 1
Разложи:
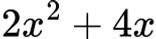
Решение:
Изнасяме общ множител →
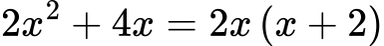
Готово – използвахме само един метод, но това е първата стъпка към комбинирането.
Пример 2
Разложи:
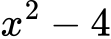
Решение:
Тук няма общ множител, но имаме формула:
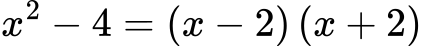
Пример 3
Разложи:
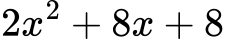
Решение:
Първо изнасяме общ множител:
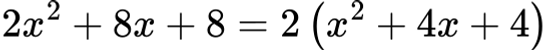
В скобите разпознаваме формулата за квадрат на сбор:
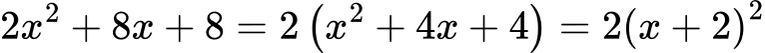
→ Комбинация: общ множител + формула.
Пример 4
Разложи:
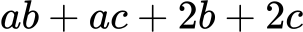
Решение:
Групираме:
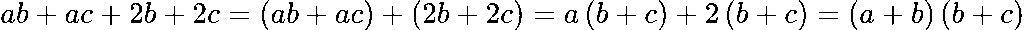
→ Комбинация: групиране + изнасяне.
Пример 5
Разложи:
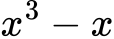
Решение:
Изнасяме общ множител:
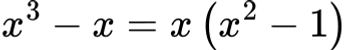
В скобите имаме разлика на квадрати:
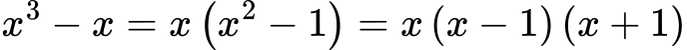
→ Комбинация: общ множител + формула.
Пример 6
Разложи:
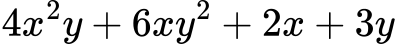
Решение:
Групираме:
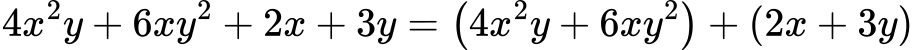
Изнасяме множители:
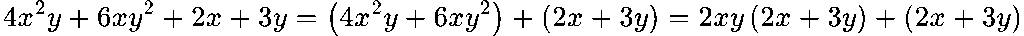
Общ множител:
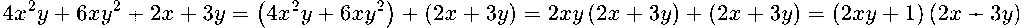
→ Комбинация: групиране + изнасяне.
3. Защо е полезно?
- Задачите често изискват повече от една техника.
- Комбинираното разлагане развива умението да „виждате скритите формули“ в изразите.
- Това умение е ключово за решаване на по-сложни уравнения, задачи с параметри и дори задачи за олимпиади.
4. Заключение
Разлагането чрез комбиниране на методи е като стратегия в игра: не винаги една стъпка е достатъчна. Понякога трябва да подредим няколко хода, за да постигнем крайното решение.
Колкото повече практикувате, толкова по-бързо ще разпознавате кой метод да използвате и как да ги комбинирате. Това е умение, което ще ви направи истински майстори в алгебрата! 🔑