Разлагане чрез групиране
Вече знаем няколко начина за разлагане на многочлени на множители – чрез изнасяне на общ множител и чрез формулите за съкратено умножение. Но какво да правим, ако даденият многочлен няма очевиден общ множител и не прилича на нито една от познатите формули? 🤔
Тогава идва на помощ друг важен метод – разлагане чрез групиране.
Той е като игра с пъзел: разделяме многочлена на групи, във всяка група търсим общ множител и после отново изнасяме. Така сложният израз се превръща в по-подреден и лесен за работа.
1. Теоретична част

Разлагане чрез групиране се използва, когато имаме многочлен с повече от два члена, в който:
- няма общ множител за всички членове наведнъж;
- можем да разделим множителите на групи и във всяка група да изнесем общ множител.
След групиране, често получаваме общ множител от втори ред, който изнасяме пред скоби.
1.1. 🔹 Стъпки при разлагането чрез групиране:

- Разделяме многочлена на подходящи групи.
- Във всяка група изнасяме общ множител.
- Ако в скобите се получи еднакъв израз → изнасяме и него като общ множител.
2. Примери с решения✅:
Пример 1
Разложи:
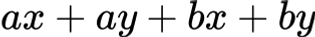
Решение:
Групираме:
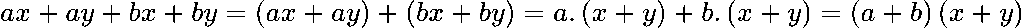
Пример 2
Разложи:
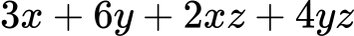
Решение:
Групираме:
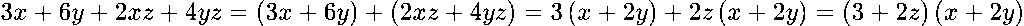
Пример 3
Разложи:
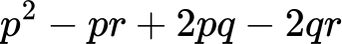
Решение:
Групираме:
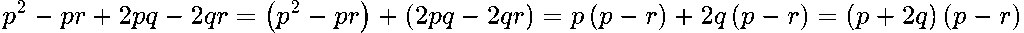
Пример 4
Разложи:
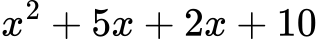
Решение:
Групираме:
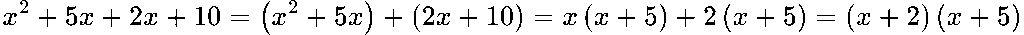
3. Защо е полезно?
- Методът на групиране ни помага да се справим с многочлени, които не могат да се разложат по друг начин.
- Често се използва в по-сложни задачи, за да подготви израза за прилагане на формулите за съкратено умножение.
- С него развиваме умението да виждаме модели и симетрии в изразите – ключово умение в алгебрата.
4. Заключение
Разлагането чрез групиране е като математическа игра за подреждане. Първо „събираме приятели“ (подходящи членове в групи), после откриваме общото между тях и накрая изваждаме наяве подредения резултат.
Запомнете: когато няма общ множител за всички членове, пробвайте да групирате! Това често е пътят към решението. 🚀