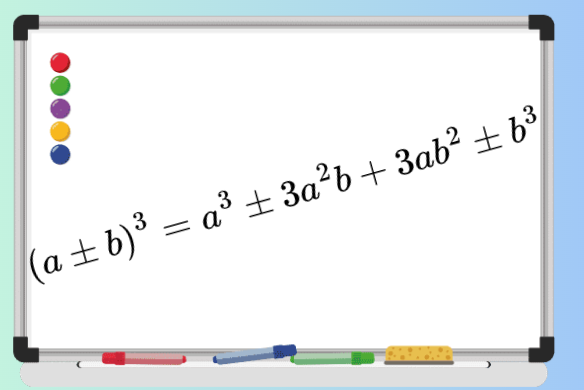Разлагане на многочлен на множители чрез формули за съкратено умножение – Продължение
Здравейте, седмокласници! В този урок ще разгледаме как се разлагат многочлени, като използваме още няколко важни формули за съкратено умножение. Ако сте пропуснали първата част, можете да я прегледате, преди да продължите ето тук: Разлагане на многочлени на множители чрез формули за съкратено умножение.
Разлагане чрез формулата a2 ± 2ab + b2 = (a ± b)2
Тази формула е позната като квадрат на сбор или квадрат на разлика. За да я използваме, трябва да открием в многочлена два точни квадрата и удвоеното им произведение.
Пример №1:
Разложете многочлена 16x4 + 24x2 + 9.
- Откриваме двата точни квадрата :
- 16x4 = (4x2)2
- 9 = 32.
- Проверяваме дали третия едночлен е удвоено произведение на двата израза, които участват с квадратите си:
- 2.4x2.3 = 24x2
- След като проверката е успешна, записваме многочлена във вида на формулата:
- 16x4 + 24x2 + 9 = (4x2)2 + 2.4x2.3 +32 = (4x2 + 3)2
Пример №2
Представате като произведение многочлена:
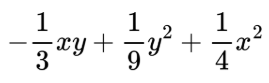
- Откриваме точните квадрати
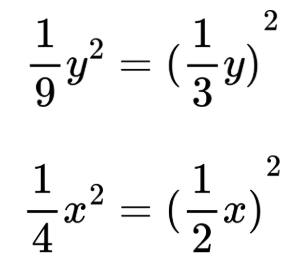
- пресмятаме удвоеното произведение на изразите, които открихме:
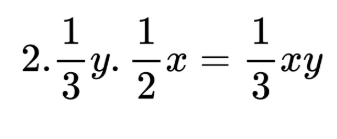
- Тъй като в многочлена знакът е минус, ще използваме формулата за квадрат на разлика на два израза:
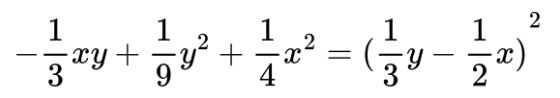

Понякога едночлените не са подредени по познатия ред. Важното е първо да откриете точните квадрати и след това да проверите за удвоеното произведение.
Пример №3
Поставете подходящ едночлен на мястото на *, така че тричлена 25a2 + 20аb + * да бъде точен квадрат.
- Откиваме точния квадрат 25а2 = (5а)2
- Виждаме, че 20ab е удвоеното произведение на (5a) и друг едночлен.
- 20аb = 2.5a.2b
- Липсващият едночлен е квадрата на 2b т.e. 4b2
- Повдигаме на втора степен едночленът, който сме открили, за да допълним до точен квадрат (5а)2 + 2.5a.2b + (2b)2 = 25a2 + 20аb + 4b2 = (5a+2b)2

Допълването на тричлен до точен квадрат е изключително важен метод, който ще използваме при разлагане на квадратен тричлен, както и при откриване на минимална и максимална стойност на израз.
Разлагане чрез формулата a3 ± 3a2b +3аb2 ± b3 = (a ± b)3
Тази формула се използва по-рядко, но е също толкова важна. При нея имаме четиричлен, в който два от едночлените са точни кубове.. Това ни помага да разпознаем формулата.
Пример №1
Разложете многочлена 8 + 36x + 54x2 +27x3.
- Откриваме двата точни куба
- 8 = 23
- 27x3 = (3x)3
- Проверяваме останалите два едночлена, за да видим дали отговарят на формулата:
- 3.(2)2.3x = 36x
- 3.2.(3x)2 = 54x2
- След като всичко съвпада, можем да запишем формулата
- 8 + 36x + 54x2 +27x3 = 23 + 3.(2)2.3x + 3.2.(3x)2 + (3x)3 = (2 + 3x)3
Да разгледаме още един пример. Този път едночлените не са подредени, както сме свикнали да ги виждаме във формулата.
Пример №2
Открийте как може да се представи като произведение многочленът 48a2y — 12ay2 + y3 — 64a3
- Откриваме точните кубове:
- y3
- 64а3 = (4а)3
- Проверяваме останалите едночлени:
- 3.y2.4a = 12ay2
- 3y.(4a)2 = 48a2y
- Забелязваме, че някои знаци са минуси. Това ни подсказва, че ще използваме формулата за куб на разлика на два израза. Трябва да внимаваме с реда на изразите. Ето как изглежда подреденият многочлен:
48a2y — 12ay2 + y3 — 64a3 = y3 — 3.y2.4a + 3y.(4a)2 — (4а)3 = (y — 4a)3
Практическо правило
Когато разлагаме многочлени с формули, следвайте тези прости стъпки:
- Пребройте едночлените:
- Тричлен най-вероятно ще се разлага с формулата за квадрат на сбор/разлика на два израза
- Четиричлен най-вероятно ще се разлага с формулата за куб на сбор/разлика на два израза
- Открийте точните квадрати или кубове: Те са най-важните елементи.
- Проверете останалите едночлени: Уверете се, че те отговарят на формулата.

Разлагането на многочлени е много полезно умение, което ще ви е необходимо и в бъдеще, например при решаване на квадратни уравнения или намиране на най-голяма и най-малка стойност на даден израз.
А сега е време за упражнения! Успех!