Приложение на пропорциите
Привет, шестокласници! Очаква ни един много интересен урок, пълен с практически задачи! Днес ще видим какво е приложението на пропорциите и къде ще са ни много полезни в живота. Да започваме!

За да можете да решите задачите, трябва да определите дали величините са свързани с права или с обратна пропорционалност.
Ако не сте уверени, прочетете тези статии : Отношение.Пропорция. и Права пропорционалност.Обратна пропорционалност.
Практически задачи с отношение
Да открием съставките в рецептата за домашна лютеница, като решим ето тази задача:

За да приготви домашна лютеница, майката на Никола закупила от пазара чушки, домати и патладжан, като теглото им се отнася както 10:7:4. Ако общото тегло на покупката е 42 kg, намерете по колко килограма от всеки зеленчук е закупила?
Отношението на зеленчуците показва, че ако разделя общото им тегло на равни части, 10 от тях ще бъдат чушки, 7 ще са домати и 4 равни части ще бъдат патладжан. Не забравяйте, че е много важна поредността на записване на отношението — тя отговаря на подредбата на зеленчуците при тяхното описание. Ако означим теглото на една от тези равни части с “x”, то за всеки от зеленчуците ще получим:
тегло на чушките: 10x
тегло на доматите: 7x
тегло на патладжаните: 4x
Съставяме уравнение за общото тегло на покупката:
10x + 7x + 4x = 42
21x = 42
x = 2
Във всяка от равните части има по 2 kg, можем да пресметнем теглото на зеленчуците:
тегло на чушките: 10x = 10.2 = 20 kg
тегло на доматите: 7x = 7.2 = 14 kg
тегло на патладжаните: 4x = 4.2 = 8 kg
Остава да направим проверка с общото тегло на зеленчуците:
20 + 14 + 8 = 42 kg

На жаргонен език казваме, че след всяко число от отношението “слагаме по един хикс” и след това съставяме уравнението.
Геометрична задача с отношение

Стефан си купил аквариум с обем 320 l. Намерете дължините на измеренията на аквариума, ако те се отнасят както 5:4:2.
Преди да запишем даденото на задачата, да отбележим две важни неща!
- Обемът е измерен в литри, трябва да го запишем в метрична мерна единица.
- Аквариумът има формата на правоъгълен паралелепипед. Измеренията му са неговите дължина, широчина и височина.
Дадено:
правоъгълен паралелепипед
V = 320 l = 320 dm3
a : b : c = 5 : 4 : 2
a,b,c = ?
Решение:
Изразяваме всяко от измеренията, като умножаваме съответните стойности от отношението с “x”.
a = 5x
b = 4x
c = 2x
Записваме формулата за обем на правоъгълен паралелепипед.
V = a . b . c
320 = 5x . 4x . 2x
320 = 40x3
x3 = 320:40
x3 = 8
x = 2
Заместваме с получената стойност на неизвестното число “x” и получаваме измеренията:
a = 5x = 5 . 2 = 10 dm
b = 4x = 4 . 2 = 8 dm
c = 2x = 2 . 2 = 4 dm
Задача с мащаб
Разстоянието между две пристанища, измерено върху географска карта, е 17,4 cm. Намерете мащаба на картата, ако в действителност двете пристанища са на 87 km едно от друго.
Когато увеличим измереното разстояние между две точки от картата няколко пъти, то и действителното разстояние между тях ще се увеличи същия брой пъти. Затова зависимостта между двете дължини е правопропорционална.
Можем да си направим една схема, за да решим по-лесно задачата. На 17,4 cm от картата отговарят в действителност 87 km. За да намерим мащаба е нужно да разберем на 1 cm от картата колко действителни сантиметра отговарят.
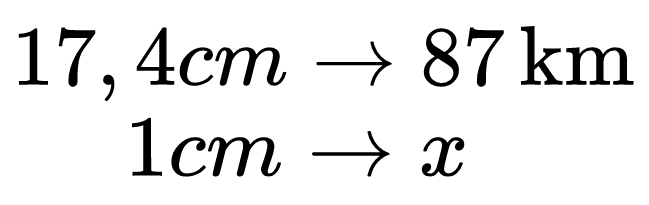
Съставяме пропорция като използваме схемата по-горе. Достатъчно е да добавим по една дробна черта между стойностите на едноименните величини:

Използваме основното свойство на пропорциите (правилото за умножение на кръст), съставяме и решаваме уравнението.

На 1 cm от картата съответства 5 km в действителност. Остава да запишем 5 km в сантиметри, за да получим мащабното число.
5 km = 5000 m = 500000 cm
Мащабното число е M 1:500 000.
Задача с пътешественици

Група от осем пътешественици решили да направят преход в Алпите. Те пресметнали колко храна им е нужна за 44 дни. Ако се присъединят към тях още трима пътешественика, за колко дни ще стигне храната?
Първо да проверим дали в тази задача имаме права или обратна пропорционалност. С увеличаването на броя на пътешествениците ще ни трябва повече храна, затова броят на дните, за които тя ще ни стигне, ще намалява. Тогава е налице обратната пропорционалност.
Правим си познатата схема:
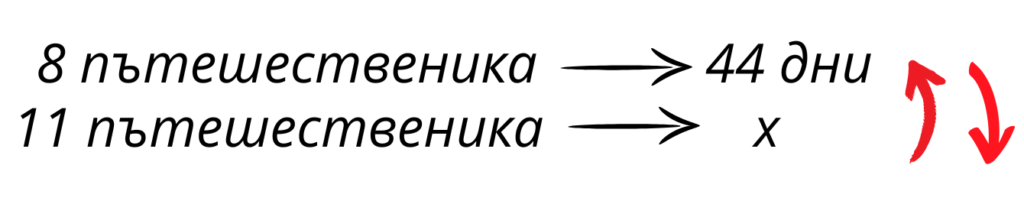
Когато съставяме пропорция при обратна пропорционалност, отново слагаме дробна черта между едноименните величини, но трябва да разменим местата на членовете на едната пропорция, ето така:

Сега използваме основното свойство на пропорциите, съставяме и решаваме уравнението:
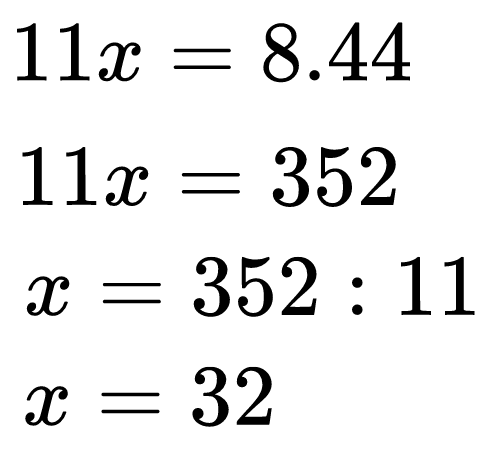
Храната ще стигне за 32 дни, ако броят на пътешествениците стане 11.

Харесаха ли ви задачите? Виждате ли колко интересна и приложима може да бъде математиката?
Време е да се упражниш със следващия тест!
Не забравяй да разгледаш и мисловната карта към урока!