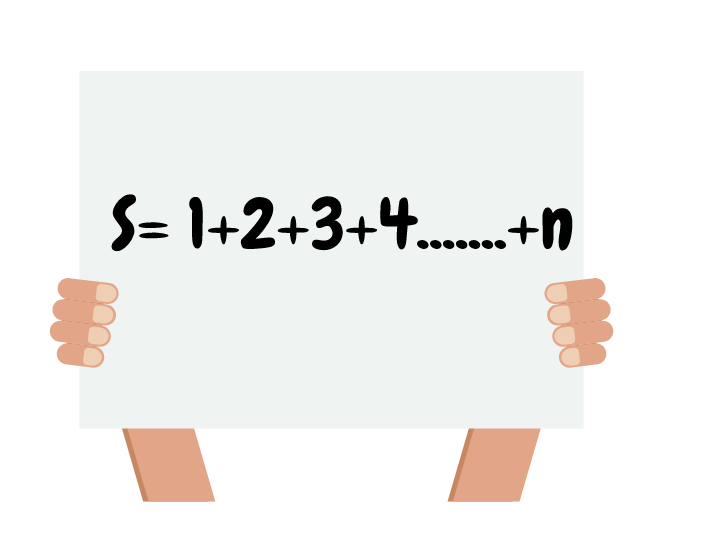Пресмятане на суми

Здравейте, малки математици! Време е да се срещнем с едни много интересни задачи! А именно-пресмятане на суми! Почти няма математическо състезание, в което да не се налага да пресмятаме суми. Затова е важно да намерим бърз и сигурен начин за това, а именно- така наречения метод на Гаус или редички на Гаус!

История с Гаус

Начинът за решаване на задачи с намиране на суми, който днес използваме, е измислен от много известен математик и физик-Карл Фрифдих Гаус! Още като малък той показвал, че може да намира интересни решения на задачите.

Гаус бил много добър ученик! Всеки път, когато учителят давал задача, я решавал за броени секунди. Затова веднъж му възложил задачата да събере всички естествени числа от 1 до 100. Детето станало готово след минута! Учителят с голяма изненада го попитал как го е направил и Гаус му показал решението. Ето какво е то:

Можем да запишем ето така сумата на числата от 1 до 100:

1+2+3+4+…………..+96+97+98+99+100

Гаус открил,че сборът на първото и последното число (1+100=101) е равен на сбора на второто и предпоследното (2+99=101). Така стигнал до извода, че всяка подобна двойка има еднакъв сбор(101). Намерил е броя на двойките (100:2=50) и го е умножил по сбора на двойките: 50.101=5050.

1+2+3+4+……….+95+96+97+99+100=5050

Днес сме благодарни на Гаус за неговия метод, който ни е много полезен!

Тогава, за да решим задачите със суми, е достатъчно да видим колко двойки имаме с еднакъв сбор и да умножим броят им по този сбор. Да опитаме да запишем подробно стъпките при решаване на задачи с намиране на сума!

Стъпки при решаване на задачите по метода на Гаус

1.Определяме броят на всички числа, които участват в сумата. Ако нашето първо число не е 1, тогава от последното число вадим първото и да прибавяме 1. Например:

5+6+7+8+……….+23+24+25

Намираме броя на числата в редичката ето така: (25-5)+1=21

2. Определяме колко на брой са всички групи (двойки числа) в редичката, които имат един и същи сбор. Тук е важно да проверим дали броят на числата в редицата е четно или нечетно число.

Ако числото е четно, като 100 например, тогава ще имам 100:2=50 двойки числа с еднакъв сбор.

Ако обаче броят на числата е нечетен, тогава отделяме последното число и го дабавяме към сумата накрая. Например, ако трябва да намерим сумата на числата от 1 до 201, ще имаме 200:2=100 двойки числа с еднакъв сбор и към него ще добавим числото 201.

3. Намираме на колко е равен сборът на числата във всяка от двойките, като съберем първото и последното число. Да видим какво ще се получи със сбор на числата от 1 до 10:

1+2+3…….+8+9+10.

Ще имаме 10:2=5 двойки числа, а сборът на числата във всяка от групичките е 10+1=11

4. Умножаваме броят на групите със сбора на числата във всяка от групите и намираме сумата. Ако сме отделили последното число, го добавяме накрая!

Да разгледаме нашия пример със сбора на числата от 1 до 201. Казахме че, имаме 200:2=100 двойки числа с еднакъв сбор и към него трябва да прибавим числото 201. Сборът във всяка група получаваме: 200+1=201. Сумата на редичката ще бъде 100.201+201=20100+201=20301.

Да видим сега два интересни примера с намиране на суми!

Задача с прочетени страници от книга

Иван има книга с 40 листа. Той е прочел половината от нея. Колко е сборът на оставащите му за четене страници?

Често се срещат задачи с прочетени странци или листове от книга. Трябва много да внимаваме с условието, тъй като всеки лист е съставен от точно две страници! Ако не ни е казано нещо различно в задачата, номерацията на страниците започва с числото 1.

Всеки лист има по 2 страници, затова имаме общо 80 страници. От тях са прочетени половината- от 1 до 40 страници. Тогава трябва да намерим ето тази сума:

41+42+43+44+………………..+77+78+79+80

Броят на всички числа в редичката е (80-41)+1=39+1=40

Тъй като получаваме четен брой групички, ще намерим направо крайната сума, без да се налага да отделяме последното число. Тогава броят на всички групички от по две числа с еднакъв сбор е 40:2=20

Сборът на всяка от двойките е равен на 41+80=121.

Крайната сума намираме като умножим броя на двойките по техния сбор: 20.121=2420

Задача с бонбони

Да видим сега една задачка с бонбони! При нея знаем сумата на числата и първото число в редичката. Трябва обаче да намерим последното.

Митко има определен брой бонбонки, които е номерирал с последователни естествени числа, започващи с 1. Сборът на числата върху всички бонбонки е 55. Колко бонбонки има Митко?

Да си представим сега как изглежда нашата редичка от числа:

1+2+3+4……+n-2 +n-1+n=55

Броят на числата е (n-1)+1=n .Тогава броят на двойките ще е n:2.

Сборът на всяка група от две числа е (1+n).

Тогава за сумата получаваме:

(n:2).(1+n)=55

Произведението на двете естествени числа е 55. Тогава единствената възможност за тези числа е да са 11 и 5. Проверяваме възможностите:

Ако n:2 е 5, а n=10. Проверяваме и другия множител: n+1=10+1=11.

Aко n:2=11, тогава n=22, a n+1=23, което не отговаря на нашето условие!

Накрая получваме, че Митко е имал точно 10 бонбона!

Харесаха ли ти задачите? Време е да се упражиш със задачите от теста!