Здравейте отново, Математковци!

Представете си, че сте архитекти на супер град и трябва да създадете къщи, паркове и улици, които са идеално подредени! Какъв по-добър начин от това да използвате правоъгълници и квадрати – форми, които са симетрични, прости и изключително важни за всякакви конструкции? Днес ще разгледаме тези две фигури, техните свойства и как да решаваме различни задачи с тях!

1. Теоретична част

1.1. Какво е четириъгълник?

Четириъгълникът е геометрична фигура, която има четири ъгъла и четири върха. Елементите на един четириъгълник (ABCD) са:

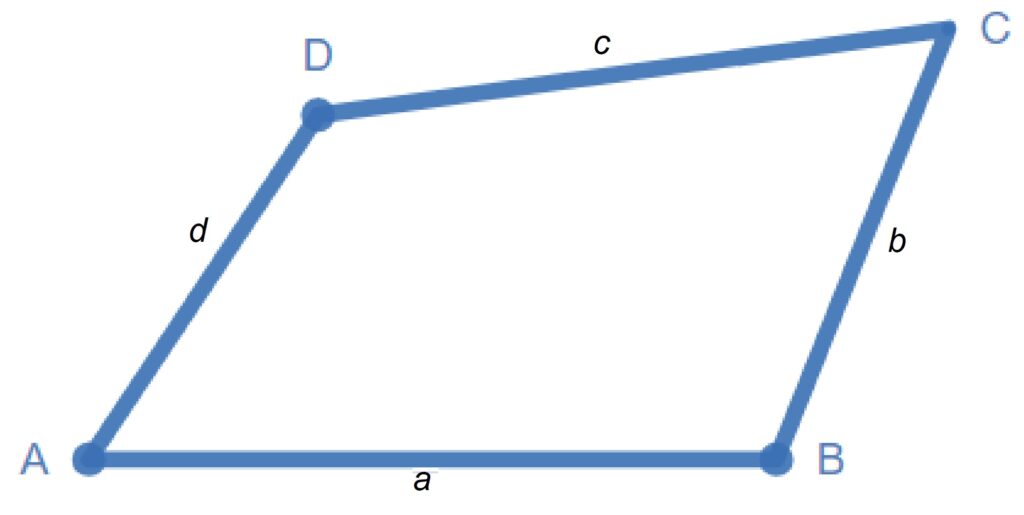
а. върхове: A, B, C и D;

б. срещуположни върхове: A и C; B и D;

в. ъгли: ∢A, ∢B, ∢C и ∢D;

г. страни: AB, BC, CD, AD;

д. диагонали: AC и BD;

е. срещуположни страни: AB и CD, AD и BC;

ж. съседни страни: AB и BC; AB и AD; BC и CD; CD и AD;

Отсечката, която съединява два срещуположни върха на четириъгълника се нарича диагонал на четириъгълника.

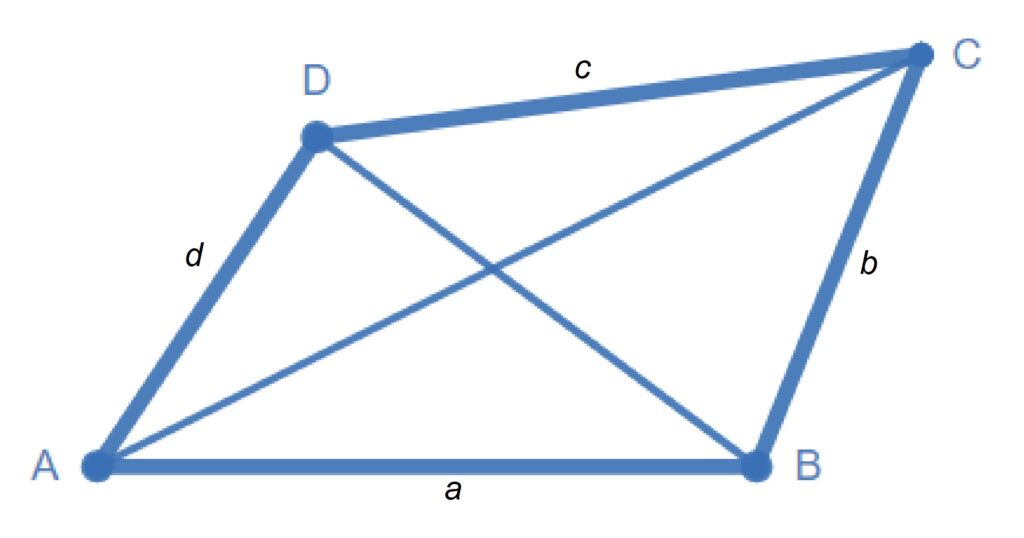
Обиколката на един четириъгълник може да се намери като:

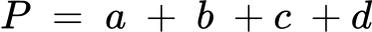
1.2. Какво е правоъгълник?

Правоъгълникът е четириъгълник с четири прави ъгъла (по 90 градуса). Две по две срещуположните му страни са равни и успоредни.

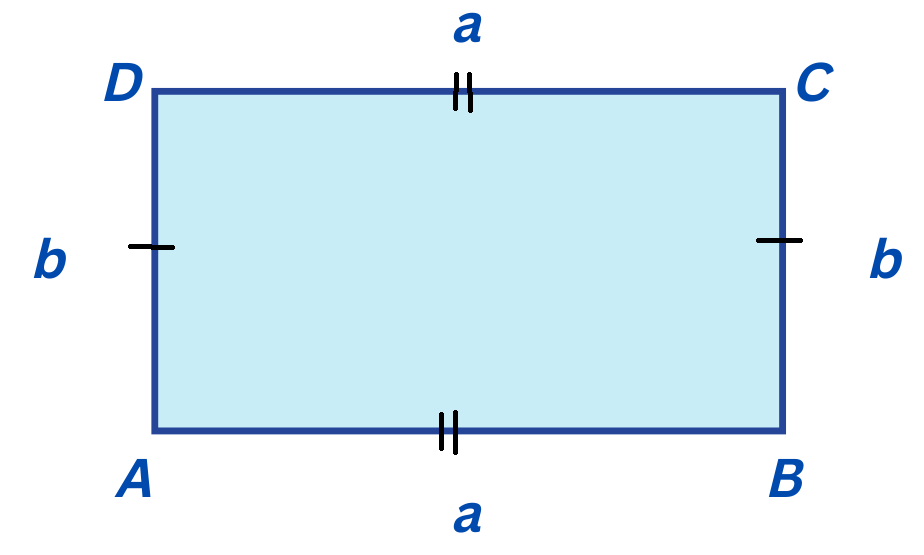
1.2. Свойства на правоъгълника:

1. Срещуположните страни са равни: AB = CD; AD = BC;
2. Всички ъгли са прави.
3. Диагоналите му се пресичат в средата и са равни по дължина.
4. Означаваме равните страни с една и съща буква. Обикновено a и b се наричат измерения на правоъгълника, където a e дължината, а b е широчината.
5. AB = CD = a; AD = BC = b;

1.3. Формули за обиколка и лице на правоъгълник:

• Обиколка: P = 2 ⋅( a + b) = 2 . a + 2 . b, където a и b са дължините на двете страни.
• Лице: S = a ⋅ b.

1.4. Какво е квадрат?

Квадратът е специален вид правоъгълник, при който всички страни са равни. Той има същите свойства като правоъгълника, но с тази особеност – всяка страна е с една и съща дължина.

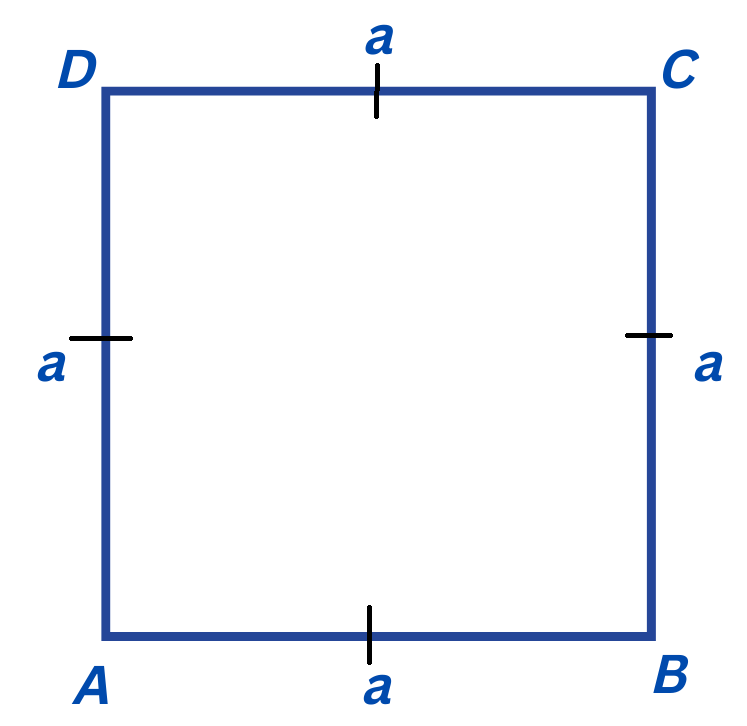
1.5. Свойства на квадрата:

1. Всички страни са равни: AB = BC = CD = AD = a
2. Всички ъгли са прави.
3. Диагоналите се пресичат в средата, образувайки прави ъгли, и са равни.

1.6. Формули за обиколка и лице на квадрат:

• Обиколка: P = 4 ⋅ a, където a е страната на квадрата.
• Лице: S = a . a.

2. Примерни задачи

2.1. Изчислителни задачи

Задача 1:
Даден е правоъгълник с дължини на страните a = 6 cm и b = 4 cm. Намерете обиколката и лицето му.

• Решение:
  • Обиколка: P = 2⋅(6 + 4) = 20 cm
  • Лице: S = 6 ⋅ 4 = 24 cm²

Задача 2:
Даден е квадрат със страна a = 5 cm. Намерете обиколката и лицето му.

• Решение:
  • Обиколка: P = 4 ⋅ 5 = 20 cm
  • Лице: S = 5 . 5 = 25 cm²

2.2. Текстови задачи

Задача 3:
Георги иска да огради правоъгълен двор с дължина 12 m и ширина 8 m. Колко метра ограда ще му трябват? А колко квадратни метра трева ще трябва да засее, за да покрие двора?

• Решение:
  • Обиколка на двора (дължината на оградата): P = 2⋅(12 + 8) = 40 m
  • Площ (лицето на тревата): S = 12 ⋅ 8 = 96 m²

Задача 4:
Ваня има парче плат с форма на квадрат със страна 12 cm. Тя иска да го раздели на 4 по-малки квадрата с равни страни. Каква ще е страната на всеки малък квадрат?

• Решение:
  • Тъй като площта на големия квадрат е S = 12 .12 = 144 cm², всеки малък квадрат ще има лице S₁ = 144 : 4 = 36 cm².
  • Страната на малкия квадрат ще бъде 36 = a . a т.е. а = 6 cm.

2.3. Практически задачи

Практическа задача 1:
Начертайте правоъгълник с дължина 10 cm и ширина 6 cm. След това начертайте квадрат със същата обиколка. Каква ще е страната на този квадрат?

Практическа задача 2:
С помощта на линийка и картон изрежете квадрат със страна 5 cm. Измерете обиколката и лицето на квадрата. Направете втори квадрат със страна, два пъти по-голяма. Сравнете обиколките и лицата на двата квадрата.

3. Заключение

Правоъгълникът и квадратът са едни от най-често срещаните форми в геометрията и ежедневието ни – от учебниците до мебелите у дома. Те са важни за изучаване, защото ни учат на основни математически принципи и ни помагат да разберем как да изчисляваме различни величини. С малко практика ще станете истински експерти в работата с тези фигури!