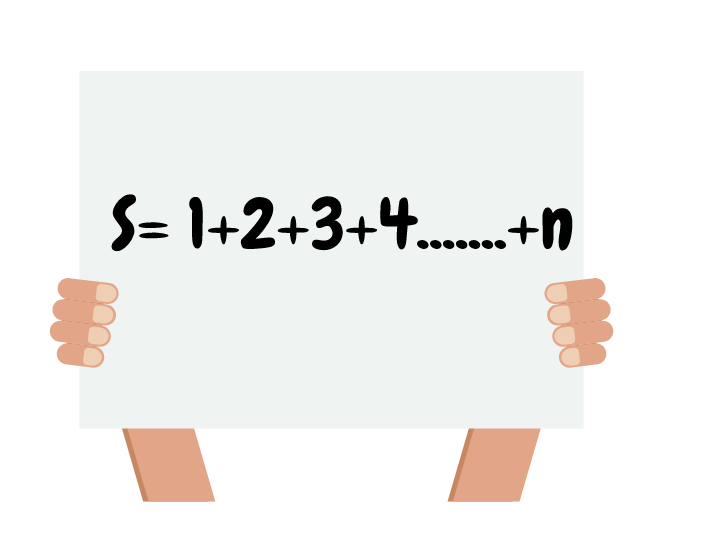Представете си кутия за обувки, тухла или шкаф – това са примери за фигури с форма на паралелепипед. Макар и да изглеждат обикновени, те крият интересни математически свойства! Днес ще се запознаем с паралелепипеда, ще разберем как да изчислим лицето на неговата повърхност и обема му, и ще разгледаме как изглежда, когато го „разгънем“.

1. Теоретична част

1.1. Какво е паралелепипед?

Паралелепипедът е геометрично тяло, ограничено от шест правоъгълника, като срещуположните му стени са еднакви и успоредни. Специален случай на паралелепипед е кубът, при който всички стени са еднакви квадрати.

1.2. Елементи на паралелепипеда

1. Стена: Паралелепипедът има 6 стени, които са правоъгълници.
2. Ръбове: Той има 12 ръба, които свързват стените.
3. Върхове: Върховете са 8 точки, в които се срещат ръбовете.
4. Размери: дължината (a), широчината (b) и височината (h) определят неговите размери.

1. Срещуположни стени – нямат общ ръб;
2. Съседни стени – имат общ ръб;
3. Основни стени – ABCD (долна) и A₁B₁C₁D₁(горна);
4. Околни стени – ABB₁A₁ и DCC₁D₁, BCC₁B₁ и ADD₁A₁
5. Основни ръбове – AB, BC, CD, DA, A₁B₁, B₁C₁, C₁D₁, D₁A₁;
6. Околни ръбове – AA₁, BB₁, CC₁, DD₁;
7. Върхове – A, B, C, D, A₁, B₁, C₁, D₁;
8. Кубът се означава: ABCDA₁B₁C₁D₁

В правоъгълния паралелепипед двойките срещуположни стени са правоъгълници, които имат едни и същи измерения. Дължините на ръбовете се наричат измерения на паралелепипеда.

Сборът от ръбовете на правоъгълен паралелепипед е:

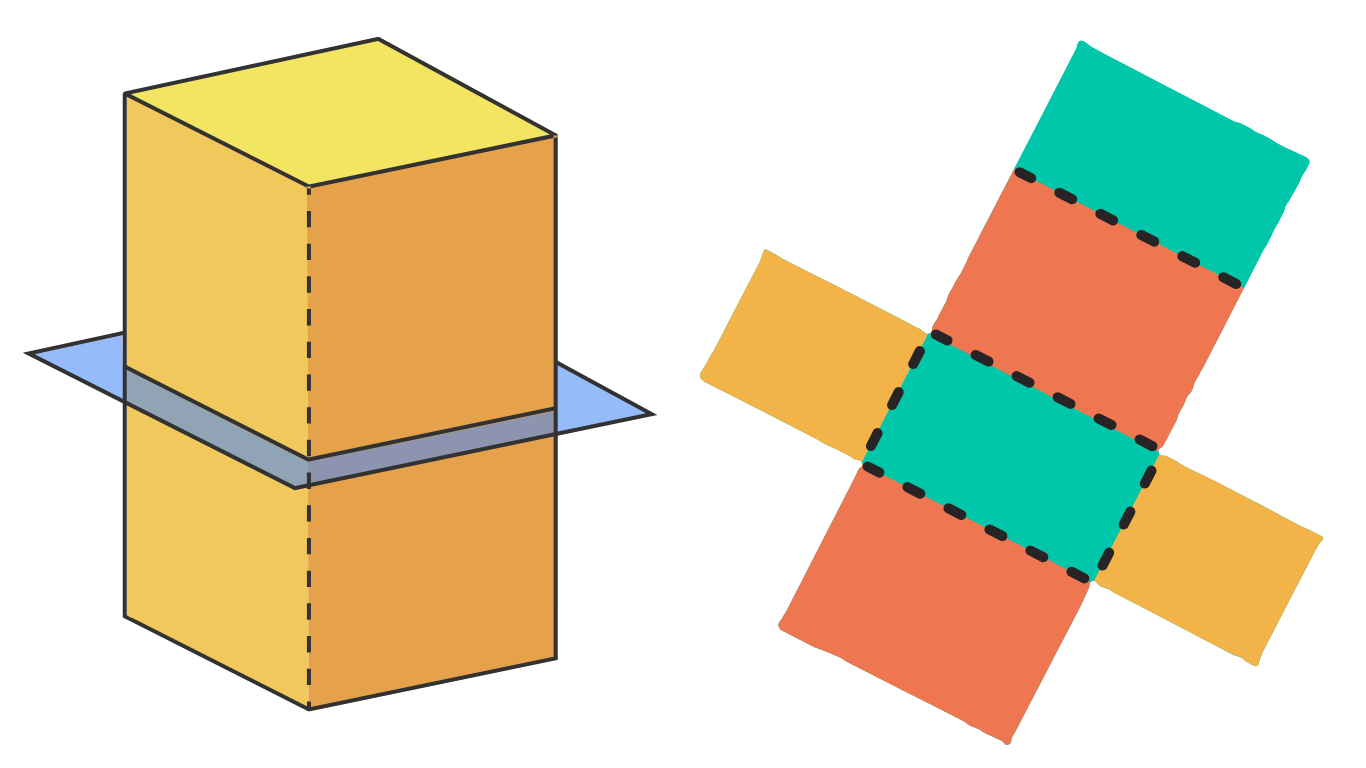
1.3. Развивка на паралелепипед

Правоъгълният паралелепипед има различни по форма развивки.

Ако разгънем паралелепипеда, ще получим шест правоъгълника, които образуват неговата развивка. Всеки от тях представлява една от стените на фигурата.

2. Формули за изчисление

2.1. Лице на повърхнина:

Ако съберем лицата на околните стени на правоъгълния паралелепипед ще, получим лицето на околната повърхнина на паралелепипеда, S.

Ако съберем лицата на всички стени на даден правоъгълен паралелепипед, получаваме лицето на неговата (пълна) повърхнина, S₁.

За паралелепипед с измерения на основата a и b, височина c и периметър P лицата на околната и пълната повърхнина са както следва:

Лицето на пълната повърхнина се изчислява по формулата:

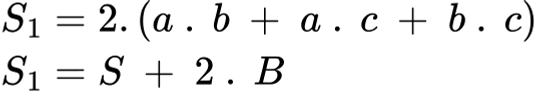
2.2. Обем на паралелепипед:

Обемът на правоъгълен паралелепипед с измерения a, b и c се намира по следния начин:

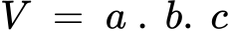
където:

от тук:

---

3. Примерни изчислителни задачи

Задача 1: Лице на повърхнина на правоъгълен паралелепипед:
Паралелепипед има дължина a = 5 cm, широчина b = 3 cm и височина c = 4 cm. Намерете лицето на повърхнината му.

Решение:

Задача 2: Обем на паралелепипед
Използвайте същите размери и изчислете обема на паралелепипеда:

Решение:

---

4. Текстови задачи

1. Опаковане на подарък:
   Кутия за подарък е с форма на паралелепипед с размери a = 10 cm, b = 6 cm и с = 8 cm. Намерете:
   • Колко квадратни сантиметра хартия ще са нужни за опаковането на кутията (без припокриване).
   • Какъв е обемът на кутията?

1. Създаване на аквариум:
   Аквариум с форма на паралелепипед има размери a = 50 cm, b = 30 cm и c = 40 cm.
   • Намерете лицето на повърхнината му.
   • Колко литра вода ще побира аквариумът? (1 литър = 1000 cm³)

---

5. Практически задачи

1. Сглобяване на модел на правоъгълен паралелепипед:
   • Начертайте развивка на паралелепипед с размери a = 6 cm, b = 4 cm, c = 3 cm.
   • Изрежете модела и го сглобете, като използвате лепило, за да залепите ръбовете му.
   • Измерете ръбовете и проверете дали всички срещуположни стени са равни.

1. Изследване на обема и повърхността на правоъгълен паралелепипед:
   • Измерете размерите на предмет с форма на паралелепипед у дома (например кутия или книга).
   • Изчислете обема и лицето на повърхнината му.

---

6. Заключение:

Паралелепипедът не е само математическа фигура – той е част от нашия свят. От кутии и шкафове до сгради и аквариуми, този триизмерен обект ни учи как да мислим пространствено и да решаваме практически проблеми. С тези задачи вие не само ще усвоите неговите свойства, но и ще го разпознавате във всичко около вас!