Правилен многоъгълник.Елементи.
Здравейте, шестокласници! Днес ще се запознаем с една много интересна и важна фигура, която има интересни разновидности — правилен многоъгълник! Ще научим кои са неговите елементи и как да ги чертаем. Да започваме!
Многоъгълник
Многоъгълникът е фигура, образувана от затворена, непресичаща се начупена линия. Ето как изглеждат многоъгълниците:

Дотук сте изучили няколко многоъгълника, заедно с техните елементи, свойства, обиколки и лица- триъгълник, правоъгълник, квадрат, успоредник, ромб, трапец. Нека да обобщим кои са елементите на всеки многоъгълник.
Елементи на многоъгълник

Можете да си припомните как се описват геометрични задачи и да изгледате видеото с основните геометрични означения в тази статия:
Да разгледаме кои са елементите на произволен многоъгълник:
- Върхове
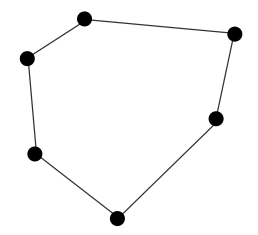
Върховете на многоъгълника са краищата на отсечките на начупената линия, която го образува.
- Страни
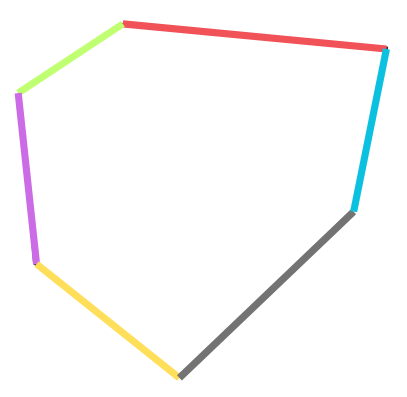
Страните на един многоъгълник са отсечките, от които се състои начупената линия, която го образува.
- Ъгли
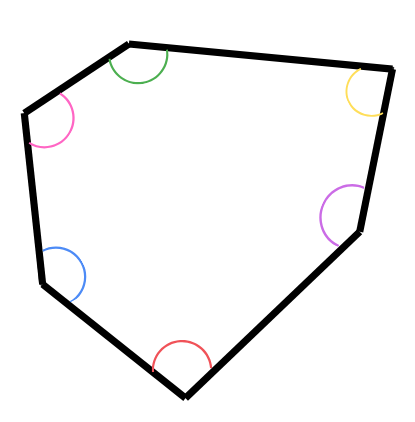
Ъглите на многоъгълника се образуват от две съседни негови страни.
- Диагонали
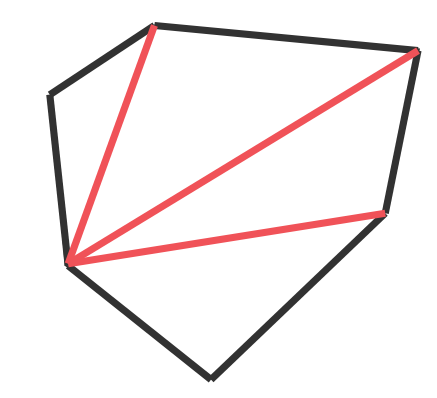
Диагоналът представлява отсечка, която свързва два несъседни върха на многоъгълника.
На чертежа са показани диагоналите, построени през един от върховете.

Единственият многоъгълник, който няма диагонали, е триъгълникът!
Можем да изчислим броя на диагоналите на всеки многоъгълник с помощта на формулата:
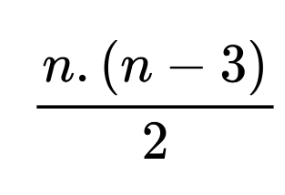
n — броят на страните на многоъгълника.
Хайде, да проверим колко са диагоналите на един четириъгълник!

Нека да разгледаме един произволен четириъгълник и неговите диагонали, за да проверим формулата.
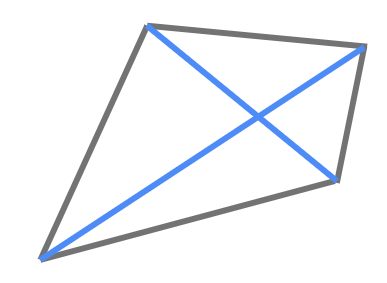
Диагоналите са наистина два. Формулата е много полезна, когато трябва да намерим броя на диагоналите на многоъгълник с много страни.
Правилен многоъгълник
Да се запознаем сега с един специален вид многоъгълник — правилен. Нека да видим как изглеждат няколко правилни многоъгълника:

Сетихте ли се кое е общото между четирите фигури?! Ако не сте — разгледайте внимателно страните и ъглите на всяка от тях.

Правилният многоъгълник е многоъгълник, на който всички страни и ъгли са равни!
Не забравяйте, трябва да са спазени и двете условия — и страните, и ъглите да са равни!
Правоъгълникът не е правилен многоъгълник, защото страните му са с различна дължина. Ромбът също не е правилен многоъгълник, защото ъглите му не са равни.
А сега, помислете как се наричат правилния триъгълник и правилния четириъгълник!

Правилният триъгълник е равностранен триъгълник, а правилният четириъгълник е квадрат!
Запомнете добре това, тъй като често се използва в геометричните задачи!
Името на останалите правилни многоъгълници съдържа броя на страните (ъглите им). Нека да разгледаме няколко правилни многоъгълника:
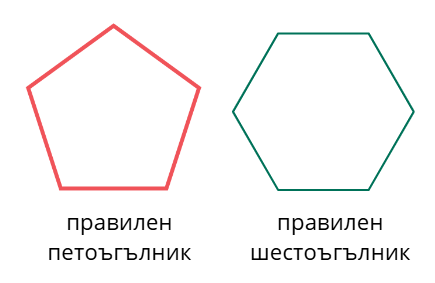
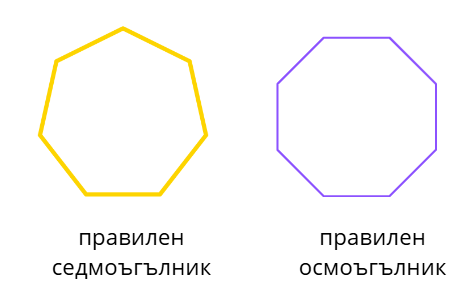
Елементи на правилен многоъгълник
Да видим освен вече посочените елементи, кои са новите само за правилния многоъгълник.
- Център
Около всеки един правилен многоъгълник може да се опише окръжност. Ето как изглежда правилен петоъгълник с описаната около него окръжност:

Центърът на окръжността се нарича център на правилния многоъгълник.
- Апотема

Когато спуснем перпендикуляр от центъра на правилния многоъгълник до негова страна, ще получим апотемата на многоъгълника. Тя разполовява страната, към която е построена. Означава се с “a“.

Апотемата може да се построи към всяка от страните на правилния многоъгълник!
- Страна
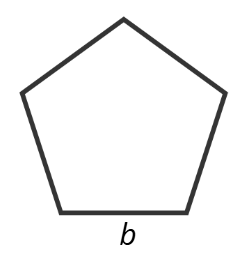
Новото тук е, че страната на правилния многоъгълник се означава с “b“.
Периметър на правилен многоъгълник
Много е лесно да намерим периметъра (обиколката) на един правилен многоъгълник, тъй като всичките му страни са равни. Достатъчно е да знаем дължината на едната страна и броя на страните. Използваме формулата:
P = n . b
P — периметър на правилния многоъгълник
n — брой на страните на правилния многоъгълник
b — дължина на страната на правилния многоъгълник
Задача №1
Намерете обиколката на правилен осмоъгълник със страна 7,5 dm.
Дадено:
b = 7,5 dm
n = 8
P = ?
Решениe:
P = n . b
P = 8 . 7,5 = 60 dm
Задача №2
Намерете вида на правилния многоъгълник, ако обиколката му е 0,225 dm, a страната му е 2,5 mm.
Дадено:
P = 0,225 dm = 22,5 mm
b = 2,5 mm
n = ?
Решение:
P = n . b
22,5 = n. 2,5
n = 22,5 : 2,5 = 225 : 25
n = 9
Фигурата е правилен деветоъгълник!

Време е да се упражните с няколко задачи, за да бъдете уверени в своите знания!