Права пропорционалност. Обратна пропорционалност
Здравейте, шестокласници! С вас вече научихме какво е това отношение и пропорция, а сега е време да видим кога ще казваме, че две величини са свързани с права пропорционалност или с обратна пропорционалност. Време е за ново приключение!

Ако искаш да си припомниш какво представляват отношение и пропорция, тогава прочети ето тази статия: Отношение. Пропорция.
Права пропорционалност

Да видим как са свързани теглото на доматите с цената за тяхната покупка.
Ако 1 kg домати струва 3,50 лв, то за 2 kg трябва да заплатим 7 лв, за 3kg —10,50 лв. Забелязахте ли, че увеличаването на теглото на доматите води до увеличаване на цената за тяхната покупка? При това колкото пъти увеличаваме теглото на доматите, толкова пъти се увеличава тяхната цена. Такива величини казваме, че са правопропорционални!

Две величини са правопропорционални, когато увеличаването (намаляването) на едната величина определен брой пъти, води до увеличаване (намаляване) на другата величина същия брой път.
Две величини x и y са правопропорционални, когато са свързани със зависимостта y = k . x, а числото k се нарича коефициент на пропорционалност и k > 0.
В нашата задача можем да означим с x цената на килограм домати, а с y — цената на покупката.
Двете величини са свързани със следната зависимост: y = 3,5 . x
Коефициентът на пропорционалност в нашия пример е к = 3,5.
Пример за права пропорционалност с геометрична задача
Да видим как са свързани лицето на правоъгълника и дължината му, ако запизим една и съща широчина. Нека нашият правоъгълник има дължина и широчина, равни съответно на 4 cm и 3 cm. Да видим как ще се промени лицето му, ако запазим широчината, а дължината се увеличи 2,4 пъти.
Дадено:
a = 4 cm
b = 3 cm
S = ?, ако а се увел. 2,4 пъти
Решение:
Лицето на правоъгълник намираме по формулата S = a . b
S = 4 . 3 = 12 cm2
Aко увеличим 2,4 пъти дължината получаваме, че:
a = 4.2,4 = 9,6 cm
Toгава лицето на правоъгълника ще е равно на:
S = 9,6.3 = 28,8 cm2
Да изчислим колко пъти е нараснало лицето:
28,8 : 12 = 2,4 пъти.

В примера увеличаването на дължината на правоъгълника 2,4 пъти води до увеличаване на лицето му също 2,4 пъти ( когато широчината на правоъгълника не са променя), затова те са правопропорционални.
В случая лицето и широчината на правоъгълника са свързани със зависимостта S = 2,4.a (да не забравяне, че широчината на правоъгълника нe се променя!). Коефициентът на пропорционалност е : k = 2,4.
Обратна пропорционалност

Да видим как са свързани величините скорост и време, когато изминатият път не се променя.
Автомобил изминава разстоянието от 180 km, като се движи със 120 km/h. За колко време ще измине същото разстояние, ако намали скоростта 1,5 пъти ?
Да запишем данните от задачата, като използваме буквените означения за величините:
Дадено:
S = 180 km
V = 120 km/h
t = ?
Решение:
Използваме формулата S = V . t
180 = 120. t
t = 180 : 120
t = 1,5 h
Ако автомобилът намали скоростта 1,5 пъти, то ще се движи със скорост:
V = 120 : 1,5 = 1200 : 15 = 80 km/h
Тогава времето, необходимо на автомобила да измине същото разстояние ще бъде:
t = S:V
t = 180 : 80 = 2,25 h
Да проверим колко пъти се е увеличило времето за движение спрямо първоначалното:
2,25 : 1,5 = 22,5 : 15 = 1,5 пъти
Намаляването на скоростта на движение 1,5 пъти води до увеличаване на времето за движение 1,5 пъти, затова те са обратнопропорционални!

Две величини са обратнопропорционални, когато увеличаването (намаляването) на едната величина определен брой пъти, води до намаляване (увеличаване) на другата величина същия брой път.
Две величини x и y са обратнопропорционални, когато са свързани с коефициент на обратна пропорционалност k с тази зависимост: к = x . y и и k > 0.
Пример за обратна пропорционалност с геометрична задача
Да се върнем на нашия правоъгълник от задачата по-горе, но нека този път да проверим как са свързани дължината и широчината на правоъгълника, ако лицето му не се променя. Нашият правоъгълник има дължина и широчина, равни съответно на 4 cm и 3 cm. Да видим как ще се промени широчината му, ако запазим лицето, а дължината се увеличи 2,4 пъти.
Дадено:
a = 4 cm
b = 3 cm
b = ?, ако а се увел. 2,4 пъти
Решение:
Намираме лицето му:
S = a . b
S = 4.3 = 12 cm2
A сега да увеличим дължината 2,4 пъти:
a = 4.2,4 = 9,6 cm
Да пресметнем каква ще бъде дължината на правоъгълник със същото лице:
S = a . b
12 = 9,6 . b
b = 12:9,6 = 120 : 96
b = 1,25 m
А сега да проверим колко пъти е намаляла широчината:
3 : 1,25 = 300:125 = 2,4 пъти

Дължината и широчината на правоъгълника са обратнопропорционални, ако не променяме лицето му, тъй като увеличаването на дължината 2,4 пъти, води до намаляването на широчината същия брой пъти!
В нашата задача двете величини са свързани със зависимостта: 12 = a . b, като коефициента на обратна пропорционалност е k = 12.
Правата и обратната пропорционалност могат да са много лесни, ако запомните как да ги различавате! За всяка практическа задача с пропорции е важно да определите правилно с какъв вид пропорционалност са свързани величините.
За да упражните урока, решете следващия тест!

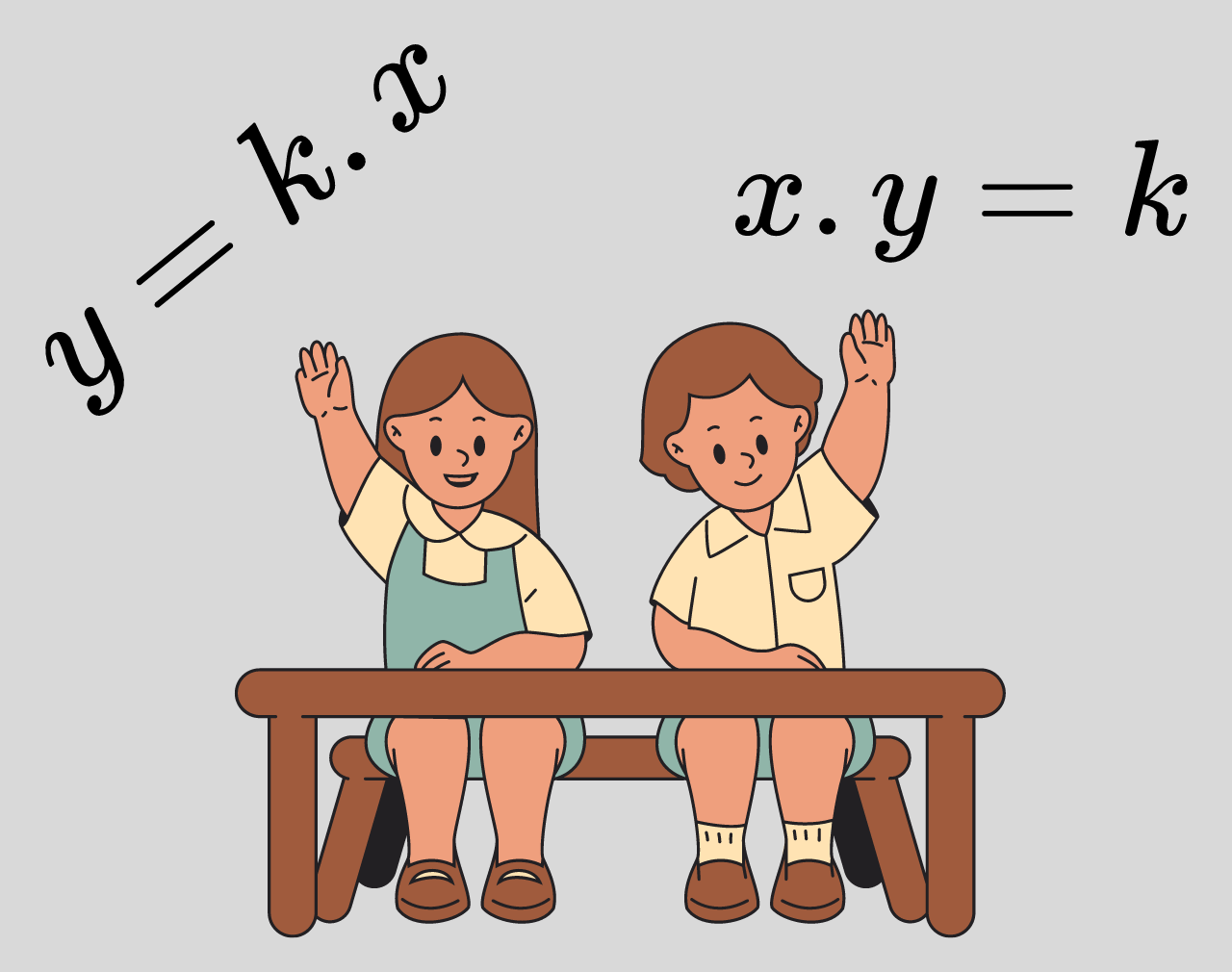






ne moga da gi razbera
На разположение сме при възникнали въпроси.