Постоянни и променливи величини. Числена стойност на израз.

Здравейте, седмокласници! Време е да се гмурнем в уроците за 7.клас. Днес ще се запознаем с някои понятия, които може би са ви познати вече. Ще разберем какво представляват постоянни и променливи величини, кои числови изрази наричаме цели и как се намира числена стойност на израз.
Постоянни и променливи величини
Постоянните величини не променят своята стойност. Наричат се още константи. Те могат да бъдат числови константи (1; 3,5; —4) или буквени константи (числото П).
Променливите величини са букви, които приемат различни числови стойности. За тях обикновено се използват последните букви от латинската азбука (x, y, z), но не е задължително. Знаете, че със същите букви означаваме и неизвестните в уравненията.
Нека съставим израз за обиколката на правоъгълник с дължина x и широчина y.
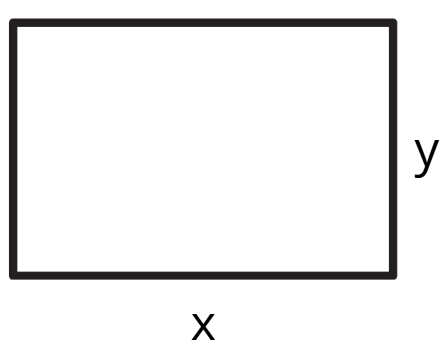
P = 2. (x + y)
В случая x и y са променливи, a 2 е константа.
Срещат се и параметри. Това са величини, които в една задача може да имат една постоянна стойност, а при други условия- друга. За параметрите обикновено се използват първите букви от латинската азбука (a,b,c…).
Нека съставим израз за броя яйца, които ще ни останат, ако в момента разполагаме с 12, а за да направим кекс са ни нужни x яйца. В хладилника ще ни останат (12— x) яйца. Ако обаче в хладилника има 20 яйца, след кекса ще ни останат (20 — x) яйца.
Ако обаче означим броя яйца с a, то след кекса ще ни останат (a — x) яйца. В израза a e параметър.

Дали в една задача с буква е означена променлива или параметър се уточнява в условието на задачата. Но все пак по подразбиране променливите се означават с x,y,z, а параметрите с a,b,c.
Цели изрази
Тази учебна година ще пресмятаме рационалните изрази и тяхната разновидност- цели изрази.
- Рационалните изрази са изрази, в които участват рационални числа и букви, свързани с вече изучените действия- събиране, изваждане, умножение, деление, степенуване. В тях може да има и скоби. Ето няколко примера:
2x+7y; 4x+(3y2+6z):3; 101-34(x+y)
- Целите изрази са рационални изрази, които не съдържат в знаменателя променлива (нямаме деление на променлива). Ако един рационален израз съдържа в знаменателя променлива, той се нарича дробен израз. Такива изрази се изучават следващата учебна година.

Не забравяйте – при целите изрази нямаме променлива с знаменателя!
Числена стойност на израз
Числената стойност на един израз намираме, когато заместим всяка от буквите, участващи в него, с числа и извършим означените действия.
Нека намерим числената стойност на израза 2x3—8y—1,5 за x = 2 и y = 1/4.
В случая можем директно да заместим буквите с тяхната числена стойност, тъй като изразът не може да се опрости повече.
Получаваме: 2.23 — 8.1/4 —1,5 = 2.8 — 2 —1,5 = 16 — 3,5 = 12,5
В някои изрази е по-удобно първо да опростим израза и след това да заместим буквите с техните стойности. Това намалява вероятността за грешки и спестява време при изчисленията. Ето един такъв пример:
Намерете числената стойност на израза 1,5x + 0,75x + 3x2 — 7x2 за x = 1/5.
Първо опростяваме израза:
1,5x + 0,75x + 3x2 — 7x2 = (1,5+0,75) x +(3 — 7)x2 = 2,25x — 4x2
Едва сега можем да заместим в израза буквата x с числото 1/5. За удобство можем да пресмятаме с десетична дроб вместо с обикновена, тъй като 1/5 = 0,2. Но дори да изчислявате с обикновена дроб, накрая ще получите същия отговор. Затова е важно свободно да работите с двата вида дроби.
Заместваме и получаваме: 2,25.0,2 — 4.0,22 = 0,450 — 4.0,04 = 0,45 — 0,16 = 0,29
Обобщение

Нека обобщим най-важното от днешния урок!
- Числовият израз представлява израз, в който участват числа и букви, свързани с действията събиране, изваждане, умножение, деление и / или степенуване.
- В числовият израз може да има константи, параметри и променливи. Обикновено за записване на параметрите използваме първите букви от латинската азбука (a,b,c), а за означаване на променливите – последните букви от латинската азбука (x,y,z).
- Намираме числена стойност на израз, когато заместим буквите със съответни числа и извършим действията.
Време е да упражните новото знание със следващия тест.