Отношение. Пропорция.
Здравейте, шестокласници! Време е да научим значението на две нови и важни математически понятия — отношение и пропорция. Да се залавяме за работа и да разберем какво се крие зад тях!

Задачите с отношение и пропорции ще са ви нужни чак до края на обучението по математика. Ще видите колко са интересни и приложими в живота!
Отношение

Когато трябва да сравним количества в определен ред, казваме, че записваме отношението им.
Ако искаме да запишем отношението на момичетата към момчетата на тази картинка, трябва да ги преброим. Тъй като момичето е само едно, а момчетата са две, записваме 1:2 (четем 1 към 2).
Редът на записване е много важен! Ако искаме да запишем отношението на момчетата към момичетата, то е 2:1 ( четем 2 към 1).

Частното на две числа се нарича отношение на тези две числа.
Записът a : b , можем да го прочетем , “a делено на b“, “a към b“, “a се отнася към b“. Можем и да го запишем като дроб a/b и да го прочетем “a върху b“.
Хайде да се упражним с една задача!

Да запишем отношението на крушите към портокалите на това изображение:
Преброяваме ги — крушите са 4, а портокалите са 6.
Записваме 4 : 6. Същото отношение ще получим, ако разделим и двете числа на 2. Крушите се отнасят към портокалите както 2 : 3 (2 към 3).
Отношение на величини в различни мерни единици
Когато записваме отношението на две или повече величини ( за дължина, тегло, сила…), трябва да внимаваме да са записани в една и съща мерна единица.
Ако искаме да напишем отношението на дължините 2 m и 30 cm, трябва да ги запишем в една и съща мерна единица за дължина. Ако изберем метри, то тогава ще получим 2:0,3. Можем да използваме свойството на частното, че то не се променя, ако умножим или разделим делимото и делителя с едно и също число. Ако умножим с 10, ще получим отношение 20:3.
Ако запишем отношението на величините, измерени в сантиметри, ще получим 200:30. Като разделим делимото и делителя на 10, получаваме отново 20:3.

Когато записваме отношение на едноименни величини, винаги проверяваме дали са в една и съща мерна единица!
Опитайте сами да запишете отношението на 210 g и 3,4 kg, като изберете едната от двете мерни единици за тегло.
Ако използваме килограми, ще получим 0,21 : 3,4 = 21 : 340.
Ако използваме грамове, получаваме 210 : 3400 = 21 : 340
Пропорция

Равенството на две отношения, наричаме пропорция.
Можем да запишем пропорцията по два начина:
a : b = c : d или a/b = c/d
Четем пропорцията така: “a се отнася към b, както c към d“, “a към b се отнася както c към d” или “отношение a към b е равно на отношението c към d“.
Числата a, b, c, d се наричат членове на пропорцията.
Хайде да видим няколко пропорции:
1 : 2 = 2 : 4 , можем да я запишем и като (1/2 = 2/4)
0,1:0,7 = 1:7 или 0,1/0,7 = 1/7
Най-лесният начин да получим пропорция , когато имаме едното отношение, е да умножим или разделим двете числа с едно и също число. Например, ако имаме отношението 3:8, за да получим пропорция, е достатъчно да умножим с 10 числата 3 и 8. Получаваме: 3 : 8 = 30 : 80.

Не бъркайте думичката “пропорция” с “порция”!
Едната думичка е математическо понятие, което има много голяма практическо приложение, а другата думичка има съвсем различно “вкусно значение”.
Основно свойство на пропорциите
Известни са различни свойства на пропорциите, но едно от тях е най-важно и приложимо, затова се нарича основно.
Първо трябва да видим как се наричат отделните членове на пропорцията.
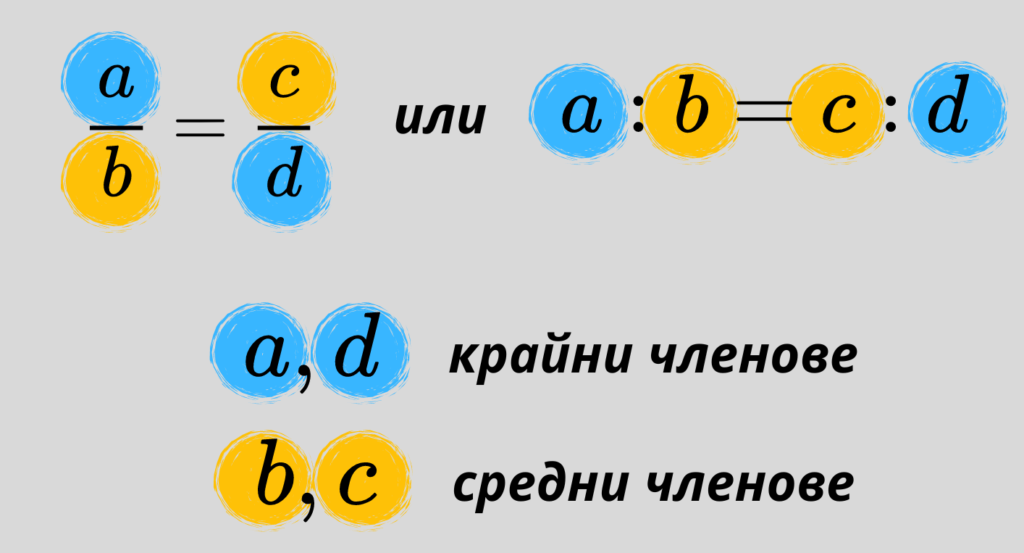
Запомнете добре разположението на крайните и средните членове на една пропорция!

Основното свойство на пропорцията гласи, че произведението на крайните членове е равно на произведението на средните членове на пропорцията:
Ако a : b = c : d, то a.d = b.c
Това свойство може да се използва, за да се провери дали дадено равенство е пропорция. Прилага се също и за намиране на неизвестен член на пропорция.
- Да проверим дали е пропорция:
1,5 : 2,5 = 3 : 5
Записваме произведенията на крайните и средните членове:
1,5 . 5 = 2,5 .3
Получаваме вярно равенство, двете отношения образуват пропорция.
- Да намерим неизвестния член на пропорцията:
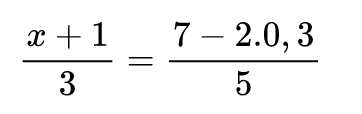
Използваме освното свойство на пропорциите и получаваме уравнение с едно неизвестно.
Можеш да си припомниш как се решава като прочетеш статиите: Правила за решаване на уравнения и По-сложни уравнения с едно неизвестно
Ето и решението:
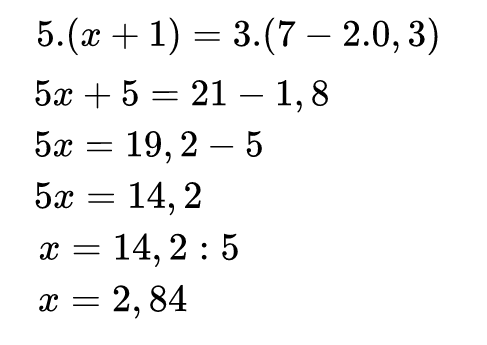

Отношението и пропорцията са много, много важни и ще ги срещате често в задачите по математика! За да сте уверени в знанията си, решете следващия тест!