Описание на геометрични задачи
Здравейте, изследователи на математиката! Днес урокът ни е много, много важен! Ще се учим да правим описание на геометрични задачи! Готови ли сте за приключение? Да започваме!

Задачите, в които участват геометрични фигури или тела, наричаме геометрични задачи.
Дотук сте изучили триъгълник, квадрат и правоъгълник. Можем да намираме техните обиколки или пък страните им!
За да решаваме задачи с геометрични фигури, е много важно да ги познаваме – да знаем как изглеждат те, колко страни и ъгли имат, имат ли равни страни, как се намира тяхната обиколка.
Стъпки при описание на геометрични задачи

Описанието на геометричната задача е като решаване на пъзел. Ако всяко парченце си е на мястото, накрая задачата е вярна и пълна. Ето и отделните стъпки, през които минаваме:
- Записваме какво ни е дадено в задачата, като си помагаме с чертеж на фигурата
- Отбелязаваме какво търсим
- Описваме подробно решението на задачата, като посочваме всички формули, които са ни нужни за него и изчисляваме с тяхна помощ
Ами да видим как ще описваме тогава задачите!
Задача с равнобедрен триъгълник
Намерете дължината на основата на равнобедрен триъгълник с обиколка 2 дм и дължина на бедрото 4 см.
Дадено:

AC = BC = 4 см
P = 2 дм = 20 см ( обиколката на фигура означаваме с буквата “P”. Записваме я в сантиметри, за да изчисляваме с една и съща мерна единица).
Търси се:
АB = ?
Решение:
P = AB + BC + AC = AB + 2.AC
Заместваме буквите с техните стойности във формулата:
20 = AB +2.4
20 = AB + 8
AB = 20-8
AB = 12 см

При описването на решението е важно да запишем формулата за обиколка и след това да заместим буквените записи с числата, на които са равни!
И не забравяйте – използваме буквата “P“ за обиколка на фигура. Може да срещнете информация, че обиколката се нарича още периметър.
Често в геометричните задачи имаме различни мерни единици и трябва да умеем да преминаваме от едната в другата мерна единица с лекота!
Задача с правоъгълник
Намерете колко сантиметра е обиколката на правоъгълник, ако едната му страна е 96 дм и е три пъти по-дълга от другата страна.
Дадено:
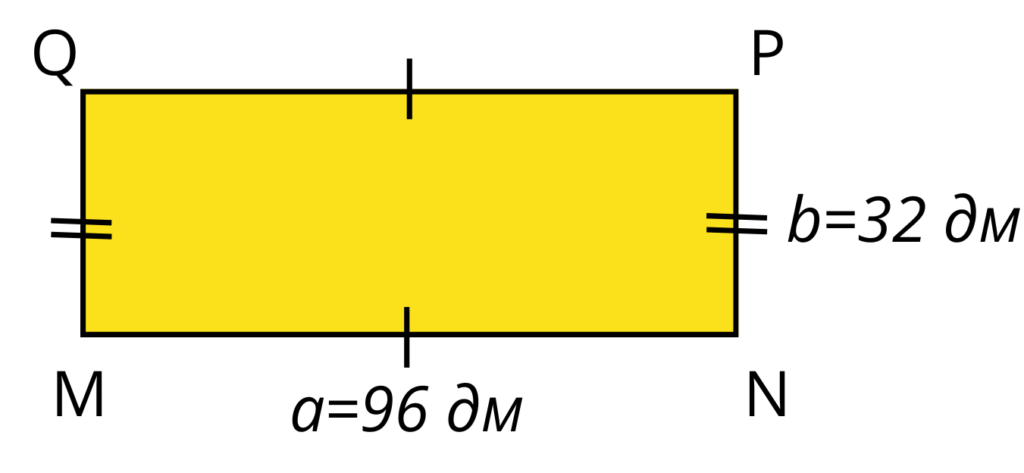
a = 96 дм
b = a:3 (другата страна е три пъти по-къса)
b = 96:3 = 32 дм
Търси се:
P = ?
Решение:
P = 2.a + 2.b
P = 2.96 + 2.32
P = 192+64
P = 256 дм = (256.10) см = 2560 см
Записваме резултата в сантиметри, както се иска в условието на задачата

Можем да запишем дължините на страните в сантиметри още, когато записваме какво е дадено в задачата. Но е по-удобно да пресмятаме с по-малки числа и чак накрая да запишем обиколката в сантиметри.
Задача с равностранен триъгълник и квадрат
Обиколката на квадрат е равна на обиколката на равностранен триъгълник. Ако страната на триъгълника е 132 см, то колко милиметра е страната на квадрата?
Дадено:
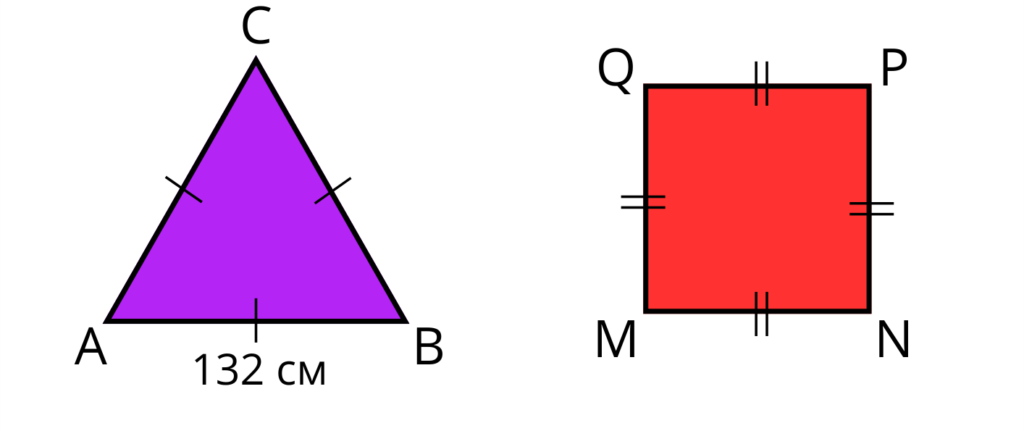
АB = BC = CA = 132 см
PABC = PMNPQ (Записваме с букви върховете на фигурата, за която се отнася обиколката, за да няма объркване между двете фигури)
Търси се:
MN = ? (Достатъчно е да запишем само едната страна на квадрата, тъй като останалите са равни на нея)
Решение:
PABC = АB + BC + CA = 3.AB
PABC = 3.132 = 396 см
PMNPQ = PABC = 396 см
PMNPQ = МN + NP + PQ + QM = 4.MN
396 = 4.MN
MN = 396:4
MN = 99 см= (99.10) мм = 990 мм

Накрая превърнахме сантиметрите в милиметри, но можем още в началото да запишем дължината на страната на квадрата в милиметри. Тогава изчисленията щяха да са с 10 пъти по-големи числа и да получим отговора направо в милиметри.
Ако искаш, опитай да решиш задачата и по този начин!
Задача с правоъгълник и квадрат
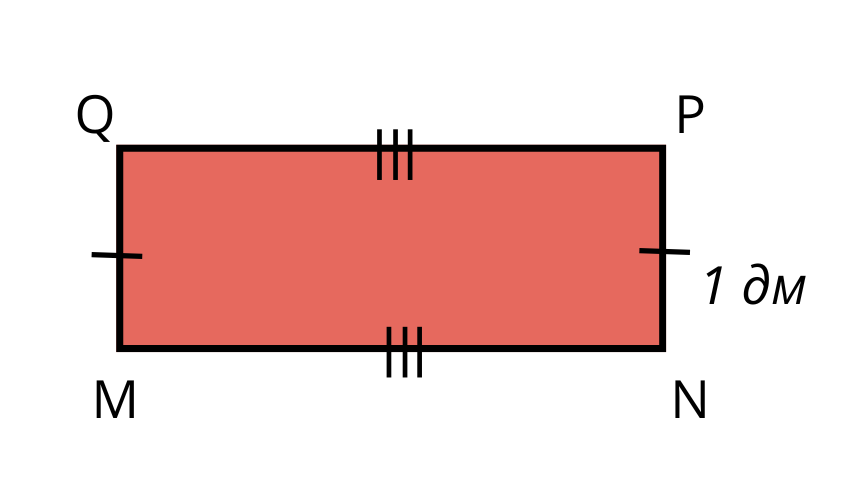
Обиколката на правоъгълник е равна на обиколката на квадрат със страна 440 мм. Ако едната страна на правоъгълника е дълга 1 дм, намерете другата му страна.
Дадено:
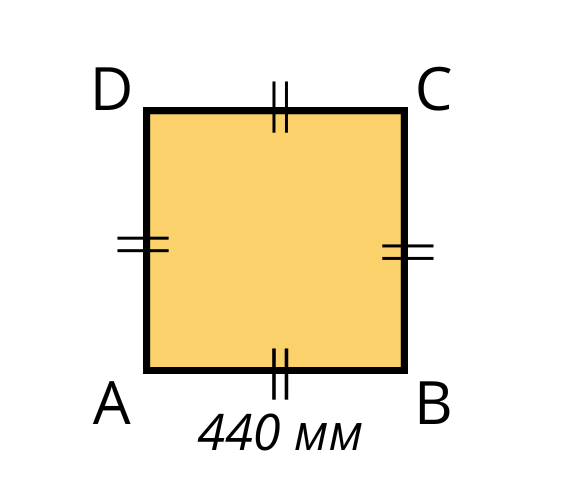
AB = BC = CD = AD = 440 мм = 44 см
PN = MQ =1 дм = 10 см
PABCD = PMNPQ
Търси се:
МN = QP =?
Решение:
PABCD = АB + BC + CD + DA = 4.AB
PABCD = 4.44 = 176 см
PMNPQ = PABCD = 176 см
PMNPQ = MN+PN+PQ+QM
PMNPQ = 2.MN+2.PN
176 = 2.MN+2.10
176 = 2.MN+20
2.MN = 176-20
2.MN= 156
MN = 156:2 = 78 см

Много е важно да извършваме изчисленията в една и също мерна единица, затова още в началото записахме дължините в сантиметри.
След като запишем формулата за обиколка, заместваме буквените означения с техните дължини.
Геометричните задачи са предизвикателни, но много, много важни! Ако се научите да ги описвате добре, винаги ще имате пълно и вярно решение! А кой не обича да се справя с предизвикателни задачи ? 😉
За да се упражните, решете следващия тест!