Окръжност. Дължина на окръжност.
Здравейте, приятели! Днес ще се запознаем отблизо с една нова геометрична фигура — окръжност! Ще научим кои са нейните елементи, както и как да намерим дължината ѝ. Време е да се впуснем в геометричните уроци на 6. клас!
Окръжност. Елементи на окръжност.

Знаете ли колко често хората бъркат фигурите окръжност и кръг? Днес ще научим много нови неща за окръжността и след това лесно ще я сравним с кръга! Ето как изглежда една окръжност:
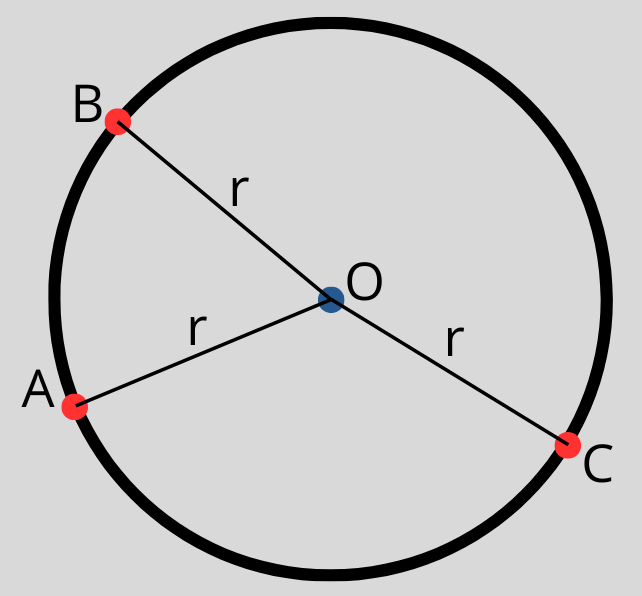
Окръжността представлява затворена линия, на която всички точки са на равни разстояния от дадена точка, която наричаме център. На нашия чертеж център е точка О, а точките A, B и C са точки от окръжността. Разстоянието, от която и да е точка на окръжността до нейния център, се нарича радиус (r). В случая отсечките OA, OB и OC са радиуси на окръжността.
Хайде да се запознаем с още елементи на окръжността освен центъра и радиуса!

Когато свържем две точки от окръжността, получавам отсечка, наречена хорда. На нашия чертеж хорди са отсечките AB, CD и MN. Забеляза ли, че едната хорда минава през центъра на окръжността? Тя има специално име — диаметър и се означава с d. Диаметърът е най-дългата хорда в окръжността и дължината ѝ е равна на два пъти дължината на радиуса на окръжността: d = 2.r
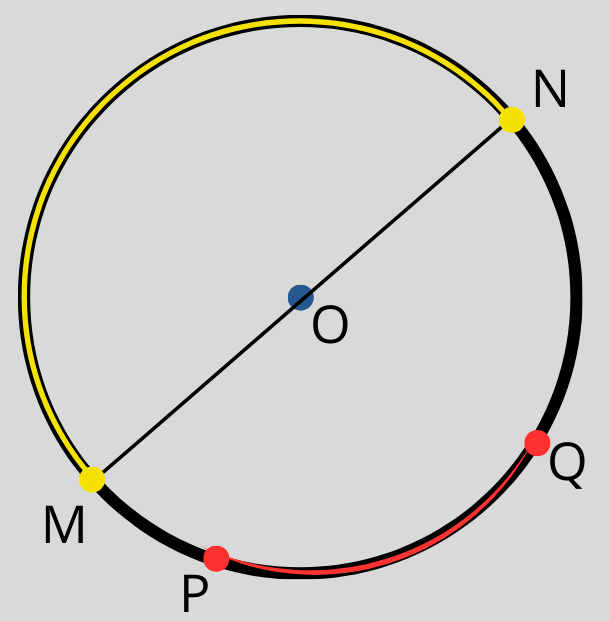
Частта от окръжността, която е заключена между две нейни точки, се нарича дъга. На чертежа са показани две дъги — между точките PQ (в червено) и между точките MN (в жълто). Точките M и N са краища на диаметър, затова дъгата, която те определят, се нарича полуокръжност.
За да е определена една окръжност, трябва да знаем нейния център и нейния радиус. За означаване на окръжност се използва буква k. Ако имаме окръжност с център точка О и радиус 6 cm, записваме: к (О, 6 cm).
Дължина на окръжност
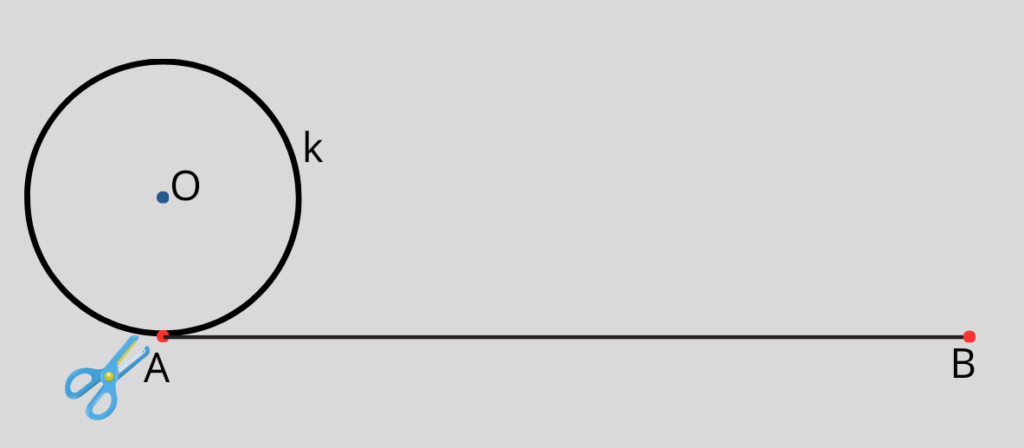
Да си представим, че сме срязали окръжността в т.А и след това сме я развили, така че да получим отсечка. Дължината на тази отсечка се нарича дължина на окръжността и се означава с C. В някои практически задачи вместо дължина, може да се използва обиколка на окръжността.
Още древните математици са установили, че когато разделят дължината на всяка една окръжност на нейния диаметър, се получава винаги едно и също число! Затова това число е константа (постоянна величина) и си има свое име — числото “Пи”. Ето как се записва с гръцка буква и на колко е равно приблизително:
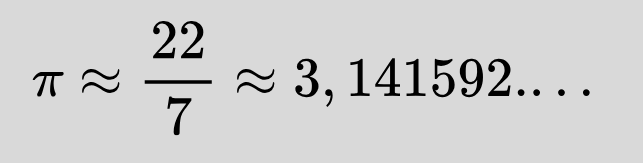
Стойността на тази константа е безкрайна, непериодична, десетична дроб. Обикновено в задачите се посочва дали да се използва стойността на числото като обикновена, като десетична дроб или да се остави като буква в крайния отговор.
Ето как са свързани дължината на окръжността с нейния радиус или диаметър:
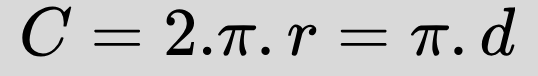

Международният ден на математиката се чества през месец март (трети месец), на 14 — то число и е свързан с приблизителната стойност на константата (приблизително 3,14).
Основни задачи с окръжност
Да разгледаме някои основни задачи с окръжност.
Задача №1:
Дадена е окръжност с радиус 5 cm. Намерете положението на точките A, B и C спрямо нея, ако те са на разстояние от нейния център съответно 4,7 cm, 6 cm и 5 cm.
Решение:
Радиусът на окръжността е разстоянието от центъра до която и да е точка от окръжността. Тъй като точка А e на 4,7 cm от центъра на окръжността, то тя е вътрешна за окръжността (ОА < r).
Точка B e на разстояние 6 cm от центъра на окръжността, което е повече от радиуса на окръжността, затова тази точка е външна за окръжността (ОB > r).
Точка C e на разстояние 5 cm от центъра на окръжността, точно колкото е дължината на радиуса ѝ. Затова тази точка лежи на окръжността (ОC = r).
Задача №2:
Изчислете диаметъра и дължината на окръжност с радиус 14 cm. Като използвате, че:

Дадено:
r = 14 cm
d = ?
C = ?
Решение:
d = 2 . r
d = 2.14 = 28 cm
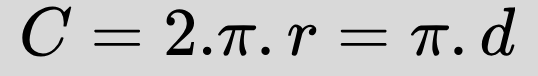
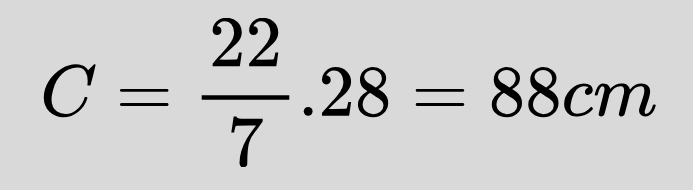
Задача 3:
Намерете радиуса на окръжност с дължина:
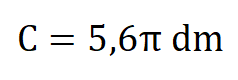
Решение:
Записваме формулата за намиране на дължина на окръжност и след това заместваме дължината с дадената стойност. Не трябва да ни притеснява, че дължината е изразена чрез константата П.Така даже ще смятаме по-малко!
Ако използваме формулата с диаметъра, после ще трябва да изчислим радиуса.
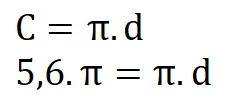
Можем да разделим двете страни на равенството на константата П и получаваме:
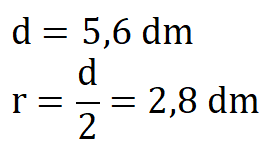
Практическа задача с окръжност

За да оградят кръгла циркова арена, са необходими 50 m рекламен плат.
А) Намерете радиуса на арената с точност до десетите.
Б) Ако цирков артист обикаля около арената със скорост от 15 km/h, за колко минути ще направи 5 обиколки?
Дадено:
C = 50 m
V = 15 km/h
r = ?
t за 5 обиколки = ?
Решение:
Нека първо намерим радиуса на арената, като използваме формулата за дължина на окръжност. Дължината на рекламния плат съответства на дължината на окръжността.
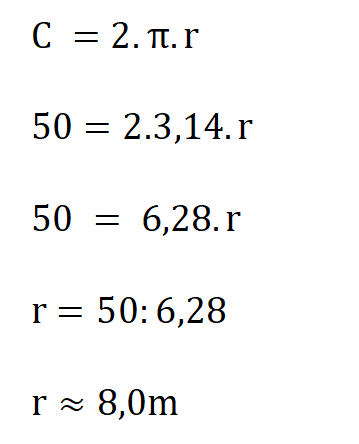
Можем да продължим с втората част на задачата. Когато имаме задачи с изминат път, трябва да използваме формулата за скорост, път и време. Тъй като цирковият артист ще обикаля арената 5 пъти, разстоянието, което ще измине, е 5 пъти по дължината на окръжността на арената.
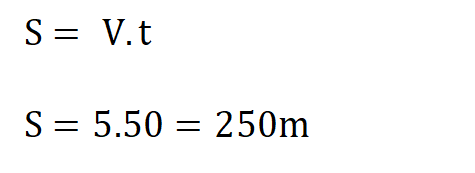
Мерните единици на величините трябва да са съпоставими, затова записваме скоростта в m/h.
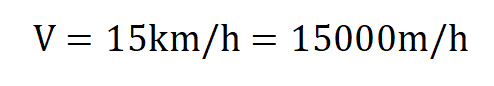
Остава да пресметнем времето:
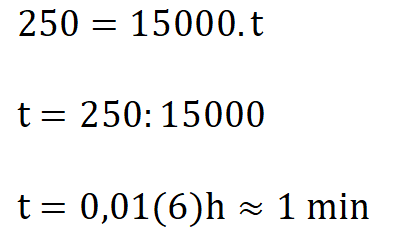
Времето пресметнахме в минути, като умножихме получената стойност в часове с 60, тъй като в 1 час имаме 60 минути.
Нашият цирков артист ще успее да направи всичките 5 обиколки за 1 минута.

Успя ли да разбереш всичко за окръжността? Време е да се упражниш с теста след урока!