Обем на прав кръгов цилиндър
Здравейте, шестокласници! Време е да вземем последният урок за цилиндър. Днес ще се научим да намираме обем на прав кръгов цилиндър и да решаваме основните задачи с него. Ще видим и практическото приложение на този вид задачи.
Обем на прав кръгов цилиндър

Може да си припомните елементите на прав кръгов цилиндър и как се намира неговата повърхнина в тези статии:
А сега да си представим, че имаме цилиндър с основа правилен многоъгълник с много на брой къси страни. Ето така:
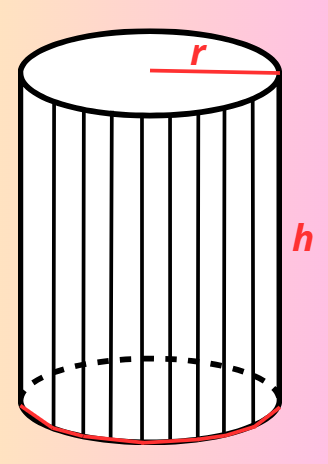
В такъв случай можем да използваме формулата за намиране на обем на права призма, за да намерим обема на прав кръгов цилиндър.

Обемът на прав кръгов цилиндър получаваме като пресметнем произведението на лицето на основата и височината му.
Достатъчно е да знаем дължините на радиуса и височината на цилиндъра, за да пресметнем неговия обем.
Основни задачи с обем на цилиндър
Задача №1
Намерете обема на цилиндъра по данните от чертежа:

Дадено:
h = 25 dm
d = 200cm
V = ?
Решение:
Трябва да работим в една и съща мерна единица за дължина.
r = d/2 = 100 cm = 10 dm
V = B.h
B = П.r2
B = П.r2 = П.102 = 100П cm2
V = 100П.25 = 2500 П cm3
Обемът може да се изразява чрез константата П, освен в задачите, в които трябва да се пресметне конкретна стойност на обема. Например колко кубични метра побира варел с формата на прав кръгов цилиндър. В този пример ни трябва конкретна стойност на обема и следва да заместим П с приблизителната стойност от 3,14.
Задача №2
Намерете височината на цилиндър с радиус 22 cm и обем 8,712П dm3.
Дадено:
r = 22 cm
V = 8,712П dm3
h = ?
Решение:
Трябва да запишем дължината на радиуса в дециметри или обемът в кубични сантиметри. Ако искаме да работим с цели числа, вторият вариант е нашият!
V = 8,712П dm3 = (8,712.1000)П cm3 = 8712П cm3
B = Пr2
B = П.222 = 484П cm2
V = B . h
8712П = 484П . h
h = 18 cm

Не забравяйте, че между съседни мерни единици за обем се преминава чрез умножение или деление на 1000.
Когато пресмятаме обеми на съдове, пълни с течности, можем да използваме думата вместимост вместо обем. Прието е обема на течности да се измерва в литри.
1l = 1 dm3
Задача №3
Намерете обема на прав кръгов цилиндър с радиус 30 cm и лице на околната повърхнина 1020П cm2.
Дадено:
r = 30 cm
S = 1020П cm2
V = ?
Решение:
S = 2Пrl
1020П = 2.П.30.l
l = 17 cm
h = l = 17 cm
B = Пr2
B = П.302 = 900П cm2
V = B . h
V = 900.П.17 = 15300П cm3
Практическа задача с обем на прав кръгов цилиндър
Фирма поръчва да се изработят 10 преспапиета със следните размери:

Дъното на преспапието е покрито с пясък, а обемът на елементите, които имитират растения, е 30 cm3. Пресметнете колко пясък и течност ще са нужни за изработката на 10 преспапиета.
Решение:
Трябва да пресметнем обемите на два цилиндъра. Единият е запълнен с пясък, а другият представлява останалата част на преспапието. Когато пресмятаме течността в преспапието, трябва да предвидим, че част от обема ще бъде зает от елементите, имитиращи растения.
Пресмятаме обема на пясъка. Той ще запълни цилиндър с височина 4 cm и диаметър — 7 cm.
B = Пr2
B = 3,14.3,52
B = 38,465 cm2
V = B.h
V = 38,465.4 =153,86 cm3
Сега да пресметнем обема на вторият цилиндър, в който ще бъде течността заедно с останалите декоративни елементи. Той има същата основа като цилиндъра, пълен с пясък, затова ще използваме вече изчисленото лице на основата. Височината на този цилиндър е 7 cm.
V = 38,465 .7 = 269,255 cm3
Остава от обема на горния цилиндър да извадим обема на декоративните елементи:
269,255 — 30 = 239,255 cm3
Последната стъпка е да умножим получените стойности по 100, тъй като ще се изработят толкова преспапиета.
153,86.100 = 15386 cm3 пясък са необходими
239,255.100 = 23925,5 cm3 течност ще е нужна за преспапиетата
Видео с още една практическа задача за обем на цилиндър

И отново е време за упражнение със следващия тест!