Обем на прав кръгов конус

Колко сладолед можем да съберем в една вафлена фунийка? Ето на този въпрос ще се научим да отговаряме днес, тъй като ще разберем как се пресмята обем на прав кръгов конус.

Изчисляване на обем на прав кръгов конус

За да разберем каква е формулата за намиране на обем на прав кръгов конус, можем да направим един експеримент! Ще ни трябват цилиндър и конус, които имат напълно равни височини и еднакви основи. Ако напълним конуса с ориз и го пресипем в цилиндъра, ще разберем, че са необходими точни три конуса, за да изпълним обема на цилиндъра.

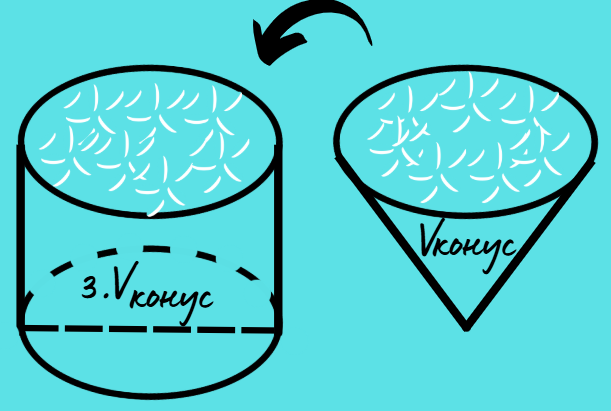
Тогава можем да направим заключението, че обемът на конуса е една трета от обема на цилиндъра, който има същата основа и равна височина. Затова можем да използваме формулата за обем на цилиндър, като разделим на три получения резултат.

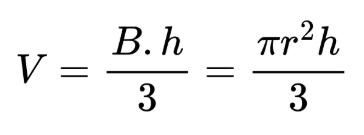
В тази формула използваме означенията:

B — лице на основата на конуса

h — височина на конуса

r — радиус на конуса (на основата му)

П — константа, приблизително равна на 3,14 или 22/7

Основни задачи с обем на конус

Задача №1

Като използвате данните за елементите на прав кръгов конус от чертежа, пресметнете неговия обем (дължините са в милиметри).

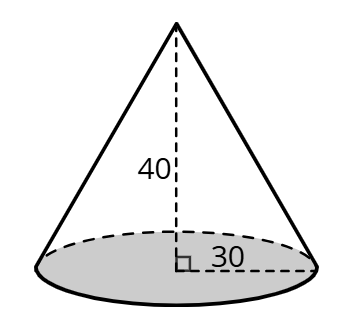
Дадено:

r = 30 mm

h = 40 mm

V = ?

Решение:

V = Пr²h/3

V = П.30².40/3

V = 12000П mm³

Задача №2

Намерете образувателната на прав кръгов конус с обем 96П cm³ и височина, равна на 0,8 dm.

Дадено:

V = 96П cm³

h = 0,8 dm = 8 cm

l = ?

Решение:

Можем да изчислим радиуса на конуса като използваме обема и височината му.

V = Пr²h/3

96П = Пr²8/3

Разделяме двете страни на равенството на константата П.

96 = r²8/3

r² = 96:(8/3)

r² = 96. 3/8

r² = 12.3 = 36

r = 6 cm

Прилагаме Питагорова теорема, за да изчислим образуващата на конуса.

h² + r² = l²

8² + 6² = l²

l² = 64+36 = 100

l = 10 cm

Практическа задача с вафлена фунийка

Магазин продава фунийки с крем. Пресметнете колко литра крем трябва да поръча магазинът, за да напълни 150 фунийки със следните размери:

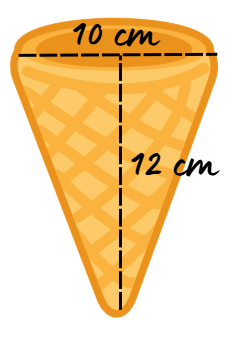
Дадено:

d = 10 cm

h = 12 cm

V = ?

Решение:

r = d/ 2

r = 10/2 = 5 cm

V = Пr²h/3

V = 3,14.5².12/3

V = 314 cm³

Остава да умножим по броя на фунийките и да запишем получения обем в литри.

150.V = 150.314 = 47100 cm³

47100 cm³ = 47,1 dm³ = 47,1 l

Практическа задача с лакомства

За парти в училище са приготвили малки изненади с лакомства, опаковани като конуси. За да ги пренесат, учителите трябва да закупят плетени кошници. Пресметнете колко кошници ще са нужни, за да може да се поберат 800 от тези лакомства. Размерете са показани на изображенията.

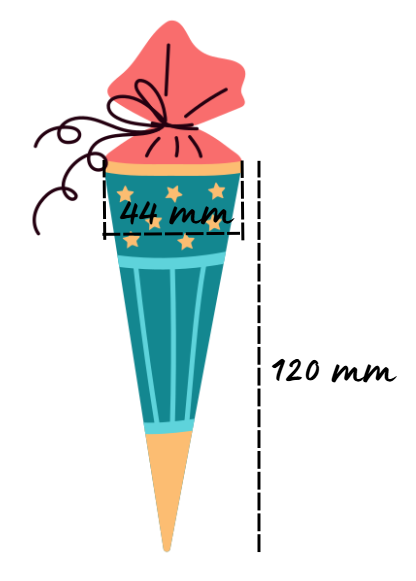
Дадено:

Елементите на конуса, в който са изненадите за учениците, са:

d = 44 mm

r = d/2 = 44/2 = 22 mm

h = 120 mm

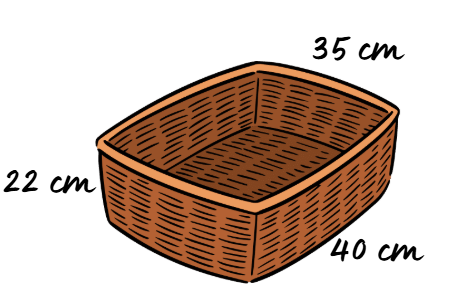
Кошницата има форма на призма, но само с една основа. Ето и нейните елементи:

a = 40 cm

b = 35 cm

h = 22 cm

Трябва да пресметнем обемите на конуса и на паралелепипеда.

V_конус = Пr²h/3

V_конус = 3,14.22².120/3

V _конус = 60790,4 mm³ = 60,7904 cm³

А сега да пресметнем обема на призмата.

V_призма = B.h

V_призма = a.b.h

V_призма = 40 . 35 . 22 = 30800 cm³

Сега пресмятаме в една кошница колко изненади с лакомства може да съберем като разделим обема на призмата на обема на конуса.

V_призма : V_конус = 30800:60,7904 = 506,66

В една кошница може да се съберат 506 лакомства. За 800 лакомства ще са нужни две кошници.

Задача с конус, издълбан в цилиндър

Едни от най-интересните задачи с геометрични тела са тези, при които се комбинират няколко тела. Следващото видео е точно с такава задача.