Обем на правилна пирамида

Здравейте, шестокласници! Време е да приключим с уроците за пирамида, като се научим да намираме обем на правилна пирамида.

Обем на правилна пирамида

Формулата за обем на пирамида можем да я изведем като направим един експеримент. За целта ще са ни нужни правилна призма и правилна пирамида, на които основите са напълно еднакви правилни многоъгълници, а височините им са равни. Ето как биха изглеждали, ако пирамидата е вътре в призмата:

Опитът се състои в това да напълним пирамидата с пясък и да го изсипем в призмата. Ще видим, че трябва да напълним и пресипем точно три пъти пясъка от пирамидата, за да се напълни изцяло призмата. Можем да направим извода, че пирамидата има обем, който е равен на една трета от този на призмата.

Основни задачи с обем на пирамида

Задача №1

Намерете обема на правилна четириъгълна пирамида с основен ръб 5 dm и височина, с 20% по-дълга от дължината на основния ръб.

Дадено:

b = 5 dm

h = 120 % b = 1,2 . 5 = 6 dm

V = ?

Решение:

Основата на пирамидата е квадрат:

B = b . b

B = 5 . 5 = 25 dm²

V = B . h / 3

V = 25 . 6 / 3 = 25 . 2

V = 50 dm³

Задача №2

Намерете височината на правилна петоъгълна пирамида с лице на основата 25,5 cm² и обем 0,102 dm³.

Дадено:

B = 25,5 cm²

V = 0,102 dm³ = 102 cm³

Решение:

V = B . h / 3

102 = 25,5 . h / 3

102 = 8,5 . h

h = 102 : 8,5 = 12 cm

Задача№3

Пресметнете основния ръб на правилна петоъгълна пирамида, ако обемът ѝ е равен на 350 m³, апотемата на основата е 7 cm, a височината на пирамидата е с 1 cm по-къса от нея.

Дадено:

V = 350 m³

а = 7 cm

h = 7 — 1 = 6 cm

b = ?

Решение:

V = B . h / 3

350 = B . 6 / 3

350 = B . 2

B = 350 : 2 = 175 m²

B = n . b . a / 2

175 = 5 . b . 7 / 2

175 = b . 35 / 2

175 = b . 17,5

b = 175 : 17,5 = 10 cm

Задача №4

По данните от чертежа намерете обема и повърхнината на правилната пирамидата, ако размерите са в метри:

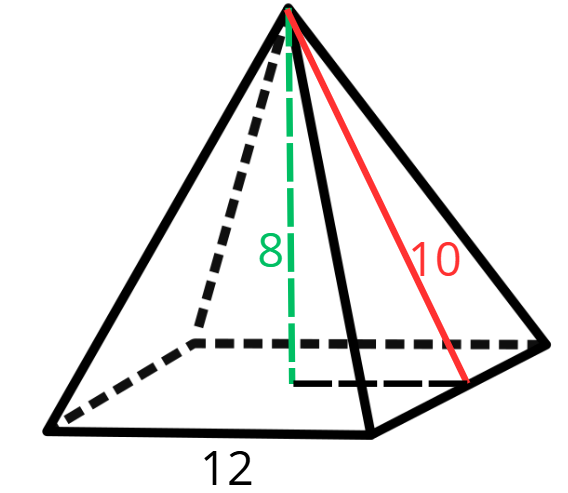
Дадено:

b = 12 m

h = 8 m

k = 10 m

V = ?

S₁ = ?

Решение:

B = b . b

B = 12 . 12

B = 144 m²

V = B . h / 3

V = 144 . 8 / 3

V = 48 . 8 = 384 m³

S = P . k / 2

S = 4 . 12 . 10 / 2

S = 240 m²

S₁ = S + B

S₁ = 240 + 144 = 384 m²

Задача с призма и пирамида

Правилна петоъгълна призма е изработена от дърво. В нея е издълбана правилна петоъгълна пирамида с основа и височина, еднакви с тези на призмата. Намерете обема на полученото тяло като използвате данните от чертежа.

Дадено:

B = 230 dm²

h = 25 dm

V_тяло = ?

Решение:

Обемът на полученото тяло е равен на разликата в обемите на призмата и пирамидата. Вместо обаче да пресмятаме двата обема и след това да ги извадим, можем да пресметнем каква част от обема на призмата ще остане, след като в нея се издълбае пирамидата. Вече говорихме, че при еднакви основи и равни височини, обемът на пирамидата е равен на една трета от обема на призмата. Тогава в нашия случай, след издълбаването, ще останат две трети от обема на призмата. Нека ги пресметнем:

V_тяло = V_призма.2/3

V_призма = B.h

V_призма = 230 . 25

V_призма = 5750 dm³

V_тяло = 5750 . 2/3

V_тяло = 3833,(3) dm³

Практическа задача с обем на пирамида

Изгледайте следващото видео, за да се упражните с още една задача.